Кузнечно-штамповочное оборудованиеРасчет коленчатого вала на усталостную прочность
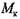 от нуля до максимума и последующим спадом вновь до нуля. При многократном повторении штамповочных операций во времени подобный характер работы пресса приводит к пульсации напряжений в металле коленчатого вала. Учитывая это обстоятельство и факты усталостного разрушения, расчет коленчатых валов следует проводить на усталостную прочность при переменном цикле напряжений. от нуля до максимума и последующим спадом вновь до нуля. При многократном повторении штамповочных операций во времени подобный характер работы пресса приводит к пульсации напряжений в металле коленчатого вала. Учитывая это обстоятельство и факты усталостного разрушения, расчет коленчатых валов следует проводить на усталостную прочность при переменном цикле напряжений.
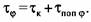
В зависимости от внутренних сил эти напряжения можно определить следующим образом:
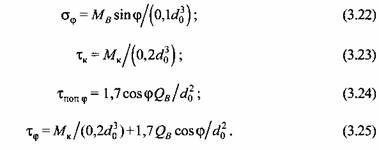
Цикличность напряжений в коленчатом вале можно оценить средними напряжениями цикла
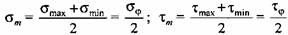
и заданными амплитудами напряжений
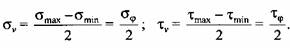
 при совместном действии нескольких нагрузок для подобного вида нагружения вычисляют по формуле при совместном действии нескольких нагрузок для подобного вида нагружения вычисляют по формуле
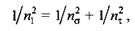
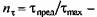
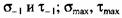 - максимальные приведенные напряжения. - максимальные приведенные напряжения.
Для определения запаса прочности по сопротивлению усталости напряжения асимметричного цикла нагружения, в том числе пульсирующего, приводят к эквивалентным напряжениям симметричного знакопеременного цикла с учетом конструктивных и технологических факторов
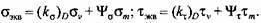
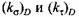 отражают влияние неравномерности распределения напряжений и их концентрации, абсолютных размеров и качества поверхности валов. Определяют их по формулам отражают влияние неравномерности распределения напряжений и их концентрации, абсолютных размеров и качества поверхности валов. Определяют их по формулам
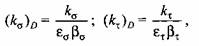
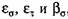
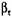 - соответственно коэффициенты, учитывающие влияние абсолютных размеров валов и качество обработки их поверхности. - соответственно коэффициенты, учитывающие влияние абсолютных размеров валов и качество обработки их поверхности.
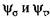 учитывающие форму диаграммы предельных напряжений, вычисляют по формулам учитывающие форму диаграммы предельных напряжений, вычисляют по формулам
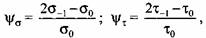
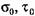 - соответственно предел усталости при изгибе и кручении (табл. 3.1). - соответственно предел усталости при изгибе и кручении (табл. 3.1).
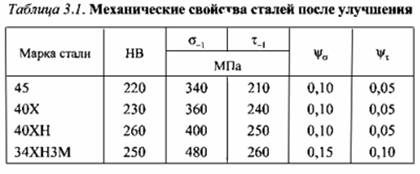
Следовательно, запас прочности при действии симметричных знакопеременных напряжений
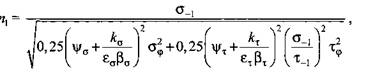
или, обозначив
получаем уравнение вида
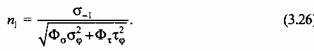 ) )
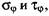 найдем найдем
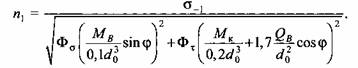
Выразим нагрузки в сечениях вала в виде однозначных функций сил на ползуне:
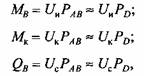
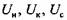 - коэффициенты. - коэффициенты.
 по усталостной прочности работы вала, можно преобразовать к виду по усталостной прочности работы вала, можно преобразовать к виду

 координации элементарного объема по отношению к главным осям. Первая производная координации элементарного объема по отношению к главным осям. Первая производная

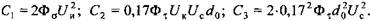
Корни этого уравнения
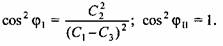
Следовательно, первая производная обращается в нуль при следующих парах значений корней:
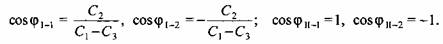
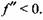
Вторая производная от подкоренного выражения в уравнении (3.27)
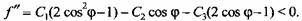
После подстановки первого и второго корней получаем соответственно
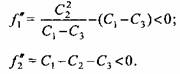
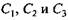 подчинены следующим условиям: подчинены следующим условиям:
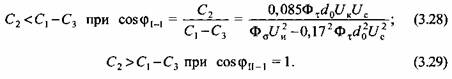
При этом действительным решением оказывается только одно из двух возможных. Границы действия решений определяются углом поворота ведущего кривошипа, при котором начинает выполняться одно из условий (3.28) или (3.29).
Решим уравнение (3.27) относительно допускаемой силы на ползуне пресса:
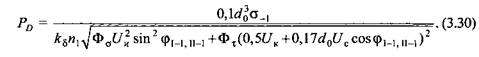
Рассмотрим частные случаи.
1. Пренебрегаем действием поперечных сил:
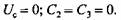
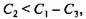 минимально допустимый запас минимально допустимый запас
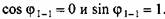 , Следователь- , Следователь-
но, уравнение (3.30) принимает вид
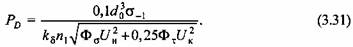
2. Пренебрегаем действием изгибающего момента:
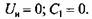
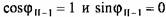 и уравнение (3.30) имеет вид и уравнение (3.30) имеет вид
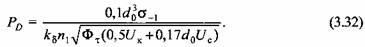
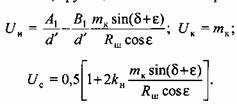 момент, крутящий момент и поперечная сила, причем момент, крутящий момент и поперечная сила, причем
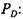
 то из уравнения (3.31) находим то из уравнения (3.31) находим
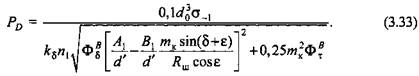
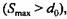 когда крутящий момент когда крутящий момент
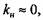 уравнения (3.32) получаем уравнения (3.32) получаем
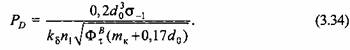
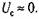 Два других коэффициента - Два других коэффициента -
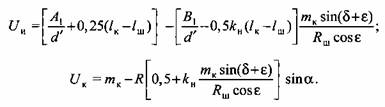
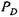 в сечении ЕЕ имеет вид в сечении ЕЕ имеет вид
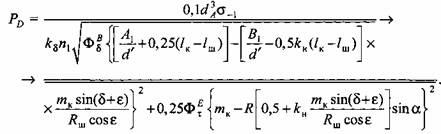
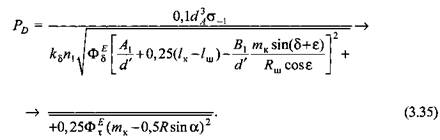
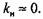 Тогда Тогда
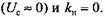 Тогда Тогда
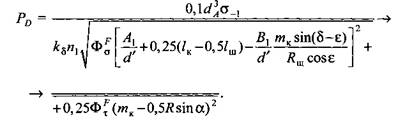
А.Ф. Нистратов рекомендует применять полные уравнения для определения допускаемой силы на ползуне только для расчета главных валов специальной конструкции, а для расчета валов типовых конструкций вполне удовлетворительные результаты дают формулы (3.33)-(3.35) в упрощенной постановке, при выводе которых пренебрегали действием некоторых силовых параметров.
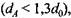 рекомендуют рекомендуют
проводить расчет на усталостную прочность и в сечении ЕЕ.
Для одноколенчатого вала с маховиком расчетные формулы для допускаемой силы на ползуне пресса имеют следующий вид:
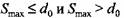 соответственно - соответственно -
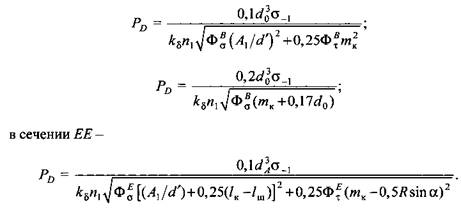
Полученные формулы для одноколенчатого вала с маховиком отличаются от выражений, установленных для предыдущей схемы, отсутствием в подкоренных выражениях вычитаемого
 отображением которой это вычитаемое является. отображением которой это вычитаемое является.
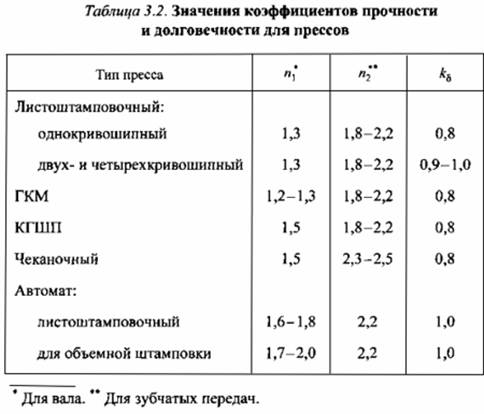
Для валов запас прочности при расчете допускаемых сил рекомендуется выбирать исходя из условий работы прессов (табл. 3.2).
|