Кузнечно-штамповочное оборудованиеРасчет насосного привода гидравлического пресса
Динамический расчет насосно-аккумуляторного привода
Насосный привод в гидравлических прессах (установках) используют для перемещения подвижной поперечины и вспомогательных механизмов - для перемещения стола, выталкивания заготовки и др. Расчеты приводов всех механизмов являются аналогичными, поэтому в дальнейшем будем рассматривать только насосный привод, осуществляющий перемещение подвижной поперечины пресса.
Задача динамического расчета - определить параметры гидравлического пресса, удовлетворяющие техническим условиям на проектирование. Такими параметрами являются скорость подвижной поперечины, номинальное усилие пресса, а также силы, создаваемые возвратными и уравновешивающими цилиндрами.
Исходными данными для расчета насосного привода являются: график деформирующей силы, приложенной к подвижной поперечине; допускаемая скорость течения жидкости в трубопроводе; характеристика рабочей жидкости; коэффициенты местных потерь и потерь по длине трубопровода.
Расчеты насосно-аккумуляторного и безаккумуляторного приводов несколько различаются между собой, а расчет привода с гидравлическим мультипликатором аналогичен расчету насосного безаккумуляторного привода с одноплунжерным насосом.
Схема насосно-аккумуляторного привода гидравлического пресса рассмотрена на рис. 6.13. Для определения сил, действующих на подвижную поперечину в процессе полного двойного хода, составим уравнения ее движения для каждого этапа: прямого холостого, рабочего и обратного холостого ходов.
Прямой холостой ход (ход приближения). Уравнение движения поперечины имеет вид
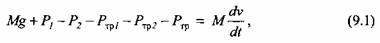
 - равно- - равно-
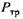 - равнодействующая сил трения в направляющих подвижной поперечины. - равнодействующая сил трения в направляющих подвижной поперечины.
Равнодействующую давления жидкости определяем как произведение соответствующих давлений и суммы площадей поперечных сечений плунжеров:

Равнодействующие сил трения в уплотнениях пропорциональны давлениям жидкости:

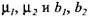 - коэффициенты трения и высота уплотнений соответственно - коэффициенты трения и высота уплотнений соответственно
в рабочем и возвратных цилиндрах.
В направляющих подвижной поперечины равнодействующую сил трения принимаем постоянной и пропорциональной силе тяжести:
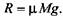
Подставив выражения (9.2) в уравнение движения (9.1), получим
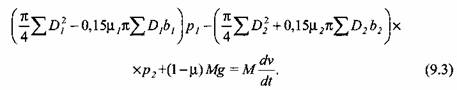
При прямом холостом ходе рабочие цилиндры пресса соединены с наполнительным баком, а возвратные - со сливным. Давление жидкости в рабочих и возвратных цилиндрах определяем, применяя уравнение Бернулли для соответствующих участков трубопровода. При этом вводим следующие упрощения в расчетной схеме:
а) клапаны открываются мгновенно;
б) ввиду малых скоростей течения жидкости в рабочем цилиндре и наполнительном баке переносное ускорение не учитываем;
в) давление жидкости в наполнительном и сливном баках считаем постоянным;
г) скорость течения жидкости в сливном баке равна нулю.
Согласно уравнению неразрывности, выразим скорости течения жидкости в трубопроводе и наполнительном баке через скорость перемещения подвижной поперечины:
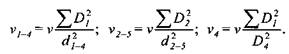
Давление жидкости в рабочих и возвратных цилиндрах при прямом холостом ходе определяем с помощью выражений, полученных после подстановок и преобразования уравнения Бернулли для участков 1-4 и 2-5 трубопровода:
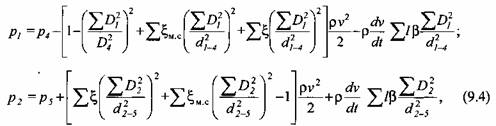
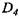 - -
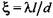 - коэффициент потерь энергии по - коэффициент потерь энергии по
длине трубопровода; / - длина трубопровода.
Подставив выражения (9.4) в уравнение движения (9.3), после преобразований получим

где А, В и С - постоянные коэффициенты:
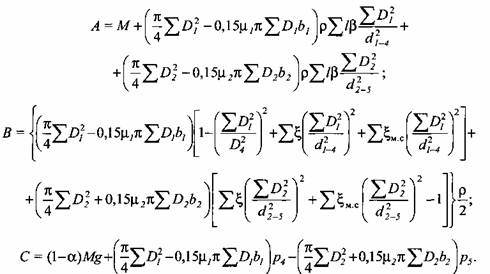
Уравнение (9.5) представляет собой частный случай уравнения Риккати, где коэффициент А характеризует приведенные к подвижной поперечине массы движущихся частей пресса движущейся в трубопроводе рабочей жидкости и сил трения в уплотнениях рабочих и возвратных цилиндров; коэффициент В - постоянное сопротивление движению подвижной поперечины; С - активные силы, приложенные к подвижной поперечине, под действием которых происходит движение.
Интегрируя уравнение (9.5), получаем формулу для определения скорости подвижной поперечины:
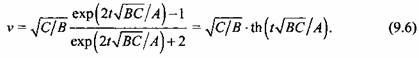
Произвольная постоянная определена из условия, что при t= 0 v = 0. При расчете гидравлических прессов обычно строят график изменения скорости в зависимости от хода подвижной поперечины. Для установления функциональной зависимости скорости v от хода S выполним следующее преобразование:
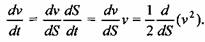
Тогда уравнение (9.5) примет вид

После разделения переменных и интегрирования получаем
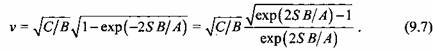
Произвольная постоянная интегрирования определена из начальных условий: при t = 0 S=0 и v = 0. Решая совместно уравнения (9.6) и (9.7) относительноS, находим
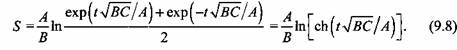
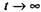 скорость подвижной поперечины скорость подвижной поперечины
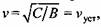 а ее движение - установившимся. а ее движение - установившимся.
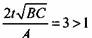 . Тогда . Тогда
 переходного процесса в приводе переходного процесса в приводе

Согласно формуле (9.9), чем меньше приведенная масса движущихся частей пресса (коэффициент А) и больше сопротивление (коэффициент В) или активная сила (коэффициент С), тем короче переходный процесс, а, согласно (9.6), чем больше активная сила и меньше сопротивление движению, тем выше скорость установившегося движения.
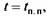 найдем путь, пройденный подвижной найдем путь, пройденный подвижной
поперечиной за время переходного процесса:

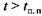 ), ),

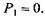 Это Это
означает, что статический напор жидкости в наполнительном баке полностью расходуется на преодоление скоростного напора и гидравлических сопротивлений на участке трубопровода 4-1 (наполнительный бак - рабочий цилиндр). При дальнейшем увеличении скорости подвижной поперечины под действием ее собственной силы тяжести произойдет разрыв струи (образование вакуума), и в результате в гидравлическую систему прессовой установки будет засасываться воздух, что недопустимо. Для предотвращения разрыва струи необходимо увеличить сопротивление со стороны возвратных цилиндров (увеличить их размеры) или повысить давление в наполнительном баке.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
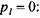
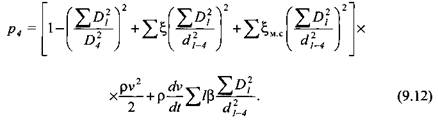
В этом случае коэффициенты в уравнении движения (9.5) будут следующими:

Тогда скорость установившегося движения подвижной поперечины

 На практике давление, соответствующее нижнему уровню поверхности рабочей жидкости в наполнительном баке, принимают на 20...30% выше полученного значения или определяют из условия заданных скоростей прямого холостого хода. На практике давление, соответствующее нижнему уровню поверхности рабочей жидкости в наполнительном баке, принимают на 20...30% выше полученного значения или определяют из условия заданных скоростей прямого холостого хода.
При наличии уравновешивающих цилиндров, которые устанавливают только в тяжелых прессах, уравнение движения (9.1) содержит еще одно слагаемое -равнодействующую давления жидкости в уравновешивающих цилиндрах.
При расчете параметров прямого холостого хода давление в наполнительном баке принимают равным наименьшему значению, при котором еще не происходит разрыва струи жидкости в трубопроводе.
Рабочий ход. Для осуществления рабочего хода необходимо соединить рабочие цилиндры пресса с жидкостью высокого давления - аккумулятором, а возвратные - со сливным баком.
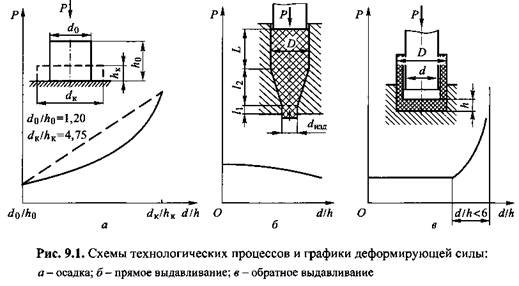
Деформирующая сила при рабочем ходе, приложенная к подвижной поперечине, не является постоянной. На рис. 9.1 показаны типовые схемы технологических операций обработки давлением и графики изменения деформирующей силы, построенные согласно приведенным ниже формулам. Так, при осадке


При прессовании (прямом выдавливании)
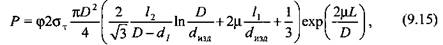
а при обратном выдавливании (закрытой прошивке)
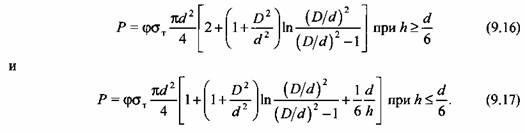
(обозначения в формулах (9.14)—(9.17) см. на рис. 9.1).
Для расчета параметров рабочего хода ковочного гидравлического пресса в качестве исходных данных выберем линеаризованный график деформирующих сил при осадке, приведенный на рис. 9.1, а. Тогда
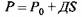
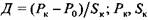
конечная деформирующая сила и ход подвижной поперечины соответственно. Уравнение движения подвижной поперечины имеет следующий вид:
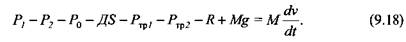
На основании уравнений Бернулли и неразрывности для участков трубопровода 1-3 (рабочие цилиндры - аккумулятор) и 2-5 (возвратные цилиндры -сливной бак), а также допущений, сформулированных при рассмотрении прямого холостого хода, находим выражения для определения давления жидкости в рабочих и возвратных цилиндрах, аналогичные (9.4):
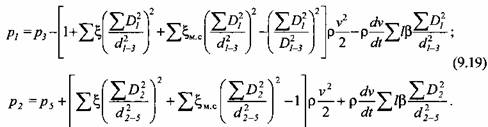
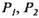 согласно формуле (9.2) и подставляя выражения для р1 и р2, согласно формуле (9.2) и подставляя выражения для р1 и р2,
приводим уравнение (9.18) к виду

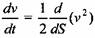 : :
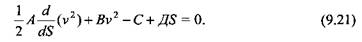
Для решения этого уравнения воспользуемся методом изменения произвольной постоянной. Интегрируя и используя начальные условия: при t = 0, s = О и v = 0, получаем
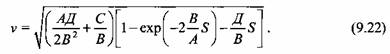
При Д = О (деформирующая сила в процессе рабочего хода постоянна) выражение для скорости подвижной поперечины (9.22) совпадает с (9.7).
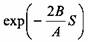 по сравнению с единицей. Тогда по сравнению с единицей. Тогда

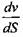 из выражения (9.22) и приравнять ее нулю. Тогда найденный ход S будет соответствовать максимальной скорости из выражения (9.22) и приравнять ее нулю. Тогда найденный ход S будет соответствовать максимальной скорости
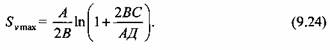
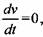 находим находим
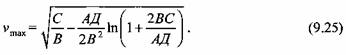
В частном случае при А = 0 и Д=0 после раскрытия неопределенности устанавливаем, что
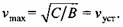
Это совпадает с полученным ранее выражением (9.13).
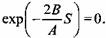 Тогда уравнение (9.22) примет вид Тогда уравнение (9.22) примет вид
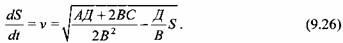
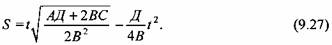
Приравнивая правые части выражений (9.23) и (9.27) и решая полученное уравнение относительно t, находим продолжительность рабочего хода
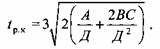
При интегрировании уравнения движения (9.21) для случая линеаризованного графика деформирующей силы с несколькими участками произвольную постоянную определяем с учетом начальных условий на каждом участке.
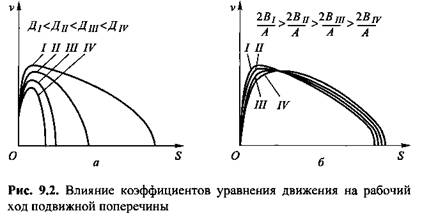
Рассмотрим влияние коэффициентов А, В, С и Д на характер изменения скорости подвижной поперечины согласно выражению (9.22). С увеличением коэффициента А при прочих равных условиях продолжительность разгона подвижной поперечины возрастает, значение максимальной скорости несколько уменьшается и смещается в сторону конца рабочего хода, длина которого возрастает. Влияние А будет сильнее проявляться при расчетах быстроходных прессов, а также прессов с низким давлением рабочей жидкости. Коэффициент А зависит от размеров трубопровода. Для уменьшения его трубопровод необходимо делать коротким.
Коэффициент В зависит от гидравлических сопротивлений и размеров трубопровода, с уменьшением В возрастает максимальное значение скорости подвижной поперечины и происходит смещение этой скорости к началу рабочего хода (период разгона сокращается). При проектировании гидравлической системы пресса нужно стремиться уменьшить сопротивление течению жидкости в трубопроводе.
С увеличением С возрастает скорость установившегося движения подвижной поперечины. Однако это целесообразно только в определенных пределах. Поскольку при достижении некоторого определенного значения С, устанавливаемого на основании энергетического расчета, происходит уменьшение КПД гидравлического пресса, такой путь повышения его быстроходности не всегда целесообразен. Для выбора рационального значения коэффициента С необходимо проводить энергетический расчет и только после этого принимать окончательное решение.
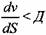 , то данная операция вообще не может быть выполнена на рассматриваемом прессе, так как по сравнению с инерционными силами сопротивление деформированию со стороны заготовки нарастает интенсивнее. , то данная операция вообще не может быть выполнена на рассматриваемом прессе, так как по сравнению с инерционными силами сопротивление деформированию со стороны заготовки нарастает интенсивнее.
Период разгона подвижной поперечины в процессе рабочего хода зависит от отношения 2 В/ А (рис. 9.2, б): чем оно больше, тем короче период разгона. Однако увеличивать его надо путем уменьшения значения А, в противном случае снижается максимальная скорость подвижной поперечины.
Обратный холостой ход. Скорость подвижной поперечины гидравлического пресса должна быть задана в технических условиях на проектирование. Задача расчета - определение силы, развиваемой возвратными цилиндрами (например, определение размеров поперечных сечений плунжеров при заданном давлении). Для осуществления обратного холостого хода необходимо соединить возвратные цилиндры с источником жидкости высокого давления - аккумулятором, а рабочие цилиндры - с наполнительным баком через наполнительный клапан или со сливным баком через главный распределитель. Для увеличения быстроходности пресса скорость обратного холостого хода должна быть максимально возможной (в некоторых случаях она достигает 60 см/с). Для определения параметров обратного холостого хода составляют уравнение движения, аналогичное (9.1) и (9.18):
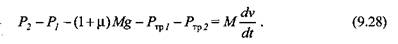
Как и в предыдущих случаях, используя уравнения Бернулли и неразрывности с принятыми допущениями, приведем уравнение движения (9.28) к дифференциальному типа Риккати:
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе

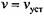 и подставить значения С и В из соотношений (9.30). и подставить значения С и В из соотношений (9.30).
Ввиду громоздкости арифметических преобразований эту задачу проще решать подстановкой.
Отметим, что в данном параграфе при рассмотрении динамики насосно-аккумуляторного привода пресса не учитывалась продолжительность срабатывания распределительных устройств.
|