Обмотока машин постоянного и переменного токаОбразование катушечных групп
До сих пор мы считали, что на каждой фазной зоне всегда находится д сторон катушек и что число пазов на полюс и фазу д равно числу катушек в каждой катушечной группе. Сейчас мы переходим к рассмотрению таких обмоток, у которых это условие на полюс не выполняется. Так как катушечная группа не может иметь дробного числа катушек, то осуществление дробного д производят, применяя катушечные группы с неодинаковым числом катушек-
Дробное д в общем случае можно представить так:
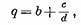
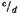 — правильная дробь. — правильная дробь.
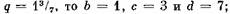 если д = если д =
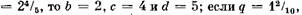 то необходимо сначала сократить дробь, а именно: то необходимо сначала сократить дробь, а именно:
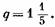
В дальнейшем будем считать, что дробная часть представляет несократимую правильную дробь, т. е. с и d не имеют общих множителей.
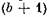 катушек в каждой, а часть — из b катушек. катушек в каждой, а часть — из b катушек.
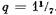 , то берут катушечные группы, состоя- , то берут катушечные группы, состоя-
щие из двух катушек (6 + 1=1 + 1=2) и одной катушки (Ъ = 1).
Так как

то для получения дробного д, мы должны взять (bd + с) соседних катушек и образовать из них в, катушечных групп. В этом случае мы получим, что на каждую катушечную группу в среднем будет приходиться по д катушек.
Пусть из этих А катушечных групп х групп будут иметь по Ъ катушек и у групп — по (Ъ + 1) катушек. Тогда
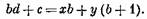
Разделим обе части уравнения на b:
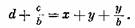
Так как х + у = д, то с/Ь = y/b, откуда у = с, х = d — у = д— с.
Таким образом, чтобы получить дробное q, мы должны взять (bd + с) соседних катушек, часть из них соединить в с катушечных групп по (b + 1) катушек, а оставшиеся катушки соединить в ((1—с) катушечных групп по Ъ катушек в каждой. Как увидим ниже, чередование тех и других катушечных групп должно происходить в определенном порядке.
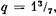 , то берем (bd + с) = 1 7 + 3 = 10 , то берем (bd + с) = 1 7 + 3 = 10
катушек и соединяем их в с = 3 катушечные группы по (Ъ + 1) = = 1 + 1=2 катушки и (d — с) = 7 — 3 = 4 катушечные группы по Ъ = 1 катушки.
Соединив таким образом первые (Ъд + с) катушек, берем следующие (Ъд + с) катушек и соединяем их так же.
Так как общее число катушек
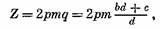
то, разделив обе части уравнения на (Ъд + с), получим
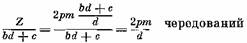
В этих уравнениях 2рт/д должно быть целым числом, иначе нельзя будет осуществить обмотку с заданным д.
Дальше вы увидим, что д или, как его обычно называют, знаменатель или показатель дробности, не должен быть кратным трем. Поэтому чтобы 2рm/d было целым числом, 2р/d должно равняться целому числу. Таким образом, при образовании катушечных групп мы должны повторять чередование из д групп 2рт/д раз.
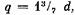 то при 2р = 14 то при 2р = 14
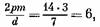
т. е. 6 чередований по д = 7 катушечных групп в каждом.
Каждое чередование имеет: с = 3 катушечные группы по (b + + 1) = 2 катушки, (д — с) = 7 — 3 = 4 катушечные группы по b = 1 катушке.
Подсчитаем, сколько катушек будет иметь обмотка.
Обозначим через А число больших катушечных групп по (Ъ + 1) катушек в каждой и через В — число малых катушечных групп по Ъ катушек в каждой.
Число больших катушечных групп А равно числу чередований, умноженному на с.
Число малых катушечных групп В равно числу чередований, умноженному на (d — с).
Число катушек равно (b+ 1) А + bВ.
Так как число чередований равно 2рт/о!, то
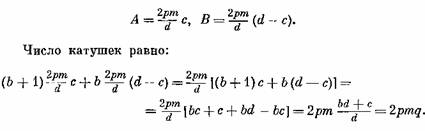
Если в предыдущем примере взять 2р = 28, то получим в два раза большее число чередований, т. е. 12.
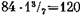 катушек. катушек.
Так как число чередований равно 2рт/d, то на каждую фазу приходится по 2р/d чередований.
Если обмотка имеет а параллельных ветвей, то, очевидно, число катушек в каждой из них должно быть одинаковым. Кроме того, э. д. с параллельных ветвей должны совпадать по фазе. Это значит, что ветви должны находиться в одинаковых точках кривой магнитного поля. Для чего необходимо, чтобы все они имели по одинаковому числу катушечных групп, состоящих как из (Ь + 1) катушек, так и из 5 катушек, и чтобы чередование и расположение их по отношению к кривой поля были также одинаковыми.
Так как на всю фазу приходится по 2р/d чередований, то на каждую параллельную ветвь будет приходиться по 2р/ad чередований.
Для того чтобы э. д. с. параллельных ветвей были равны, 2р/аd должно быть целым числом.
Таким образом, при дробном q выбор числа параллельных ветвей становится более ограниченным, чем при целом д.
Так, например, в четырехполюсной машине при целом д можно было сделать 1, 2 и 4 параллельные ветви, при дробном же q, при d = 2 можно сделать только 1 и 2 параллельные ветви, а при d= 4 только 1 параллельную ветвь.
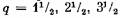 и т. д., то с = 1 и т. д., то с = 1
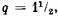 чередование: чередование:
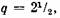 чередование: (2, 3) (2, 3), (2, 3) чередование: (2, 3) (2, 3), (2, 3)
и т.д. (цифры в скобках означают число катушек в группе, а скобки отделяют чередования).
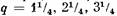 и т. д., то в каждом чередовании будет и т. д., то в каждом чередовании будет
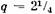 чередование: (2, 2, 2, 3), (2, 2, 2, 3), (2, 2, 2, 3) и т. д., чередование: (2, 2, 2, 3), (2, 2, 2, 3), (2, 2, 2, 3) и т. д.,
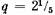 чередование: (2, 2, 2, 2, 3), (2, 2, 2, 2, 3), (2, 2, 2, чередование: (2, 2, 2, 2, 3), (2, 2, 2, 2, 3), (2, 2, 2,
2, 3) и т. д.
Если числитель дроби с не равен единице и не равен (д. — 1), то чередование больших и малых катушечных групп можно определить следующим способом.
Составляем таблицу из с строк и d столбцов. Начиная с верхней строки первого столбца, вписываем в таблицу с чисел, равных (b + 1). Затем (с? — с) чисел, равных b, потом снова с чисел (Ъ + 1) и (д. — с) чисел бит. д., пока не будут заполнены все d столбцов. Порядок заполнения показан стрелками на примерах:
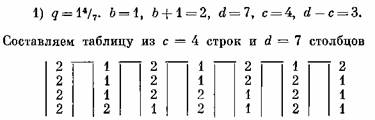
Чередование катушечных групп можно брать по любой строке, например по верхней: 2, 1, 2, 1, 2, 1, 2.
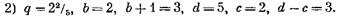
Составляем таблицу из двух строк и пяти столбцов:
3 2 2 3 2 3 2 3 2 2
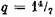 таблица будет иметь три строки: таблица будет иметь три строки:

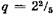 таблица будет иметь три строки: таблица будет иметь три строки:
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
2 3 2 3 2 2 3 2 2 3 2 2 3 2 3
Чередование катушечных групп можно брать по любой строке.
|