Обмотока машин постоянного и переменного токаОбмотки с неравновитковыми катушками
При расчете обмоток встречаются случаи, когда число витков фазы не делится без остатка на число катушек фазы или когда в двухслойных обмотках на катушку приходится не целое число витков. Тогда (имея в виду двухслойные обмотки) обычно одну половину комплектов катушек делают с одним числом витков, а другую с числом витков на 1 или 2 больше. Если по ширине паза лежит один активный проводник, то берут в одной части катушек на один виток больше, чем в другой. Если же по ширине паза лежат два активных проводника, то берут на два витка больше.
Для лучшего использования паза большие и малые катушки нужно располагать так, чтобы число проводников в нем было одним и тем же. На практике катушки располагаются или согласно рис. 2-109, а, когда они чередуются через один паз, или согласно рис. 2-109, б, когда они попарно чередуются через два паза. Шаг катушек должен быть таким, чтобы в пазу одна сторона принадлежала катушке с большим числом витков, а другая — с меньшим. При укладке катушек по рис. 2-109, а шаг катушек

должен быть нечетным, а при укладке по рис. 2-109, б — четным.
При первом способе укладки число катушек должно быть четным, так как число больших и малых катушек должно быть одинаковым. Но в двухслойных обмотках число катушек равно числу пазов, поэтому получим:
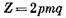 — четное число или, так как 171=3, — четное число или, так как 171=3,
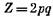 — четное число, или — четное число, или
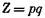 — целое число. — целое число.
При втором способе укладки число катушек должно быть кратным четырем, так как каждой паре малых катушек должна соответствовать пара больших катушек. Поэтому при втором способе укладки
 — число, кратное 4, или — число, кратное 4, или
2рq — число, кратное 4, или
рд — четное число.
Так как при целом д произведение рq всегда равно целому числу, то первый способ укладки применим во всех случаях. Второй способ, требующий четного шага, применим только в тех случаях, когда рq = четному числу, т. е. когда или р, или д равны четному числу.
При образовании параллельных ветвей необходимо в каждую из них включить по одинаковому числу одинаковых катушечных групп. Только тогда э. д. с. ветвей будут одинаковыми по величине.
Рассмотрим сначала образование параллельных ветвей при первом способе укладки.
Ввиду того, что нижние стороны катушек располагаются в таком же порядке, как и верхние, достаточно в дальнейшем рассмотреть расположение только одних верхних сторон.
При четном числе катушек в группе (рис. 2-110) все катушечные группы получаются одинаковыми. Так, например, при q=2 все группы имеют по одной большой и по одной малой катушке,

причем расположение катушек также одинаково. Поэтому в каждой фазе э. д. с катушечных групп, сдвинутых между собой на двойной полюсный шаг, будут одинаковыми по величине и направлению, а э. д. с катушечных групп, сдвинутых между собой на полюсный шаг, равны и противоположны по направлению. Таким образом, в отношении э. д. с катушечных групп такая обмотка с целым q ничем не отличается от нормальной двухслойной обмотки с целым числом пазов на полюс и фазу. В связи с этим при образовании параллельных ветвей необходимо, чтобы число катушечных групп

делилось без остатка на число параллельных ветвей, т. е. 2р!а было равно целому числу.
При нечетном числе катушек в катушечной группе (рис. 2-111) одинаковые катушечные группы чередуются через одну. Так, например, при q=5 все нечетные катушечные группы имеют по три больших и по две малых катушки, причем малые катушки располагаются между большими. Все четные катушечные группы, наоборот, имеют по три малых и по две больших катушки, причем большие катушки располагаются между малыми. Вследствие

этого э. д. с нечетных катушечных групп будет больше э. д. с. четных катушечных групп.
Таким образом, в отношении э. д. с. катушечных групп обмотки с нечетным д напоминают обмотку с дробным числом пазов на полюс и фазу при знаменателе (d=2, т. е. для образования параллельных ветвей должно быть выполнено условие:
 — целое число. — целое число.
Рассмотрим обмотки, у которых катушки располагаются по второму способу.
При q = 2 одинаковые катушечные группы располагаются через одну. Так, например, на рис. 2-112, а все нечетные катушечные группы оказались большими, а четные — малыми.
Таким образом, в отношении распределения катушечных групп эта обмотка напоминает обмотку с дробным числом пазов на полюс при знаменателе (d=2, т. е. для образования параллельных ветвей р/d должно быть равно целому числу. Такое же распределение катушечных групп получим при q —6.
При q=4 (рис. 2-112, в) все катушечные группы по числу больших и малых катушек и по их расположению оказываются одинаковыми. Поэтому образование параллельных ветвей производится так же, как и в нормальных обмотках с целым числом пазов на полюс и фазу.
При q=3 (рис. 2-112, б) одинаковые катушечные группы чередуются через четыре группы. Так, например, катушечные группы 1, 5,9,13 и т. д. имеют по две большие катушки с левой стороны и одну малую с правой стороны. Если же взять катушечные группы 3, 7, 11 и т. д., также одинаковые между собой, то э. д. с. их будет меньше, чем у катушечных групп 1, 5, 9, 13 и т. д., так как первые группы имеют меньшее число витков.
Катушечные группы 2, 6, 10 и т. д., хотя и имеют такие же катушки, как и катушечные группы 7, 5, 9,13 и т. д., но вследствие другого относительного расположения больших и малых катушек на фазных участках э. д. с. катушечных групп 2, 6,10 и т. д. будут равны по величине, но не равны по фазе э. д. с групп 1,5,9, 13 и т. д.
Катушечные группы 4, 8, 22 и т. д. имеют такие же катушки, как катушечные группы 3, 7, 11 и т. д., но вследствие другого относительного расположения больших и малых катушек э. д. с.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
катушечных групп 4, 5, 12 и т. д. будут равны по величине, но не равны по фазе э. д. с. групп 3, 7, 11 и т. д.
Таким образом, э. д. с. катушечных групп одной фазы, например, первой /1, 4, 7, 10/ будут различными. Если же взять катушечную группу 13 этой же фазы, то ее э д. с. будет совпадать по величине и фазе с э. д. с. катушечной группы 1 и соответственно 16 с 4,19 с 7 и 22 с 10,
Каждая фаза обмотки, имея всего 2р катушечных групп, при д—3 будет иметь группы четырех видов, причем число катушечных групп одинакового вида будет равно 2рт/12. Так, например, в четырехполюсной машине будет всего катушечных групп 2рт=4 • 3=12 по 2p=4 в каждой фазе. Так как все четыре катушечные группы имеют неодинаковое э. д. с, то их можно соединять только последовательно, т. е. при 2р=4 а=1.
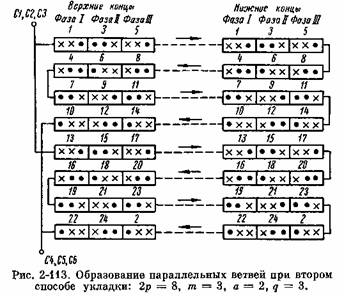
При 2р=8 в каждой фазе будет по 2р=8 катушечных групп.
 в каждой фазе будет по две одинаковые катушечные группы. Следовательно, в этой обмотке можно получить а=2 (рис. 2-113). в каждой фазе будет по две одинаковые катушечные группы. Следовательно, в этой обмотке можно получить а=2 (рис. 2-113).
При q=5 (рис. 2-112, г) одинаковые катушечные группы чередуются через четыре группы. В связи с этим образование параллельных ветвей происходит аналогично предыдущему.
В общем случае при нечетном q отношение р/а должно быть четным числом.
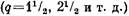 как обмоток, наиболее как обмоток, наиболее
часто встречающихся в асинхронных двигателях.

Первый способ укладки. Катушечные группы (рис. 2-114) получаются четырех видов, причем одинаковые катушечные группы повторяются через четыре группы:

В каждой фазе одинаковые катушечные группы расположены через 12 катушечных групп, или через 12/m=4 полюсных шага. Так как т соответствует

то одинаковые катушечные группы фазы располагаются через число пазов, соответствующее 4 т, т. е.

Таким образом, при образовании параллельных ветвей должно быть выполнено условие:

 и а=2 изображена на рис. 2-115. и а=2 изображена на рис. 2-115.
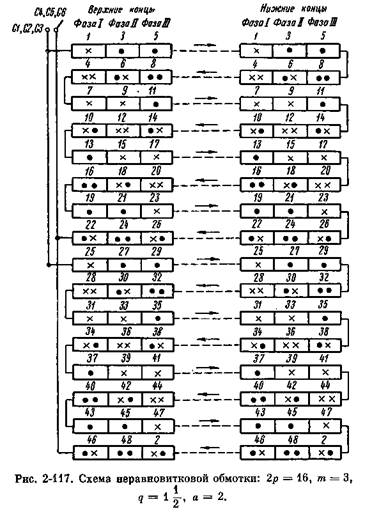
Второй способ укладки. Катушечные группы (рис. 2-116) получаются шести видов, причем одинаковые по

виду и чередованию катушечные группы повторяются через восемь групп:

В каждой фазе одинаковые катушечные группы располагаются через 24 группы, т. е. через 8 полюсов.

Таким образом, при образовании параллельных ветвей должно быть выполнено условие:
 — целое число — целое число
 и а=2. Для более равномерного распределения катушечных групп по статору можно в одну параллельную ветвь включить последовательно группы (для I фазы): 1, 7, 13, 19, 28, 34, 40, 46 и в другую: 4,10,16, 22, 25, 31, 37, 34. Аналогично и для II и III фаз. и а=2. Для более равномерного распределения катушечных групп по статору можно в одну параллельную ветвь включить последовательно группы (для I фазы): 1, 7, 13, 19, 28, 34, 40, 46 и в другую: 4,10,16, 22, 25, 31, 37, 34. Аналогично и для II и III фаз.
|