Паровые турбины. Часть 1Относительный лопаточный кпд
Относительный лопаточный КПД ступени представляет собой отношение работы ступени #ы, развиваемой 1 кг пара, к ее располагаемой энергии Я0:
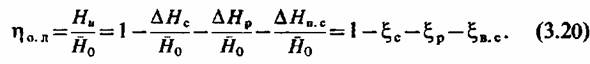
Здесь коэффициентами обозначены относительные величины потерь. При этом следует отличать потери в решетках с и р, рассмотренные в гл. 2 и отнесенные к располагаемой энергии данной решетки, от потерь ^с и ^р, отнесенных к располагаемой
энергии всей ступени Я0.
 * , когда в числителе остается выражение для работы данной ступени, а в знаменателе вместо Н0 подставляется Я0 — 0,5с 2: * , когда в числителе остается выражение для работы данной ступени, а в знаменателе вместо Н0 подставляется Я0 — 0,5с 2:

 Тогда Тогда
 ) )
 . Этот случай представлен в А, ^-диаграмме на . Этот случай представлен в А, ^-диаграмме на
 , то обычно полезно в этой ступени может использоваться , то обычно полезно в этой ступени может использоваться
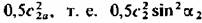
 * согласно (3.21), а несколько иная величина КПД: * согласно (3.21), а несколько иная величина КПД:
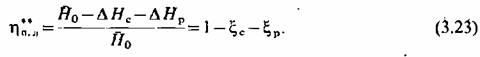
Используя формулы (3.7), (3.16) и (3.20), находим

Эта формула показывает, что в общем случае КРЩ находится в довольно сложной зависимости от скоростей парового потока и их направлений.

где Сф—некоторая фиктивная скорость. Тогда можно написать
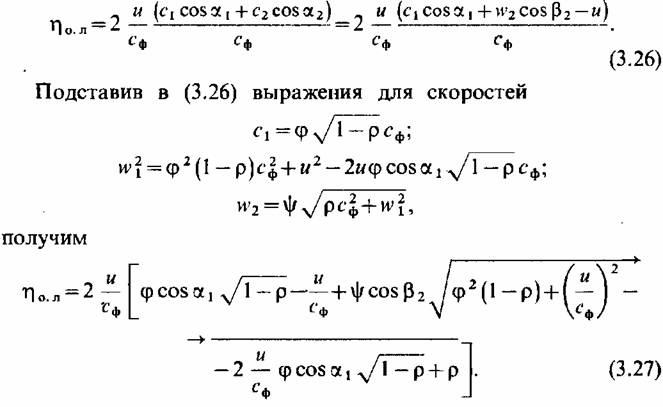

В некоторых частных случаях выражение для КПД принимает более простую форму.
Рассмотрим, например, чисто активную ступень (р = 0). Тогда выражение для относительного лопаточного КПД можно преобразовать следующим образом:

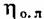 имеет максимум. имеет максимум.
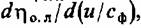 приравняем ее нулю и получим приравняем ее нулю и получим

Отсюда определяем максимальное значение относительного лопаточного КПД чисто активной ступени (р = 0):
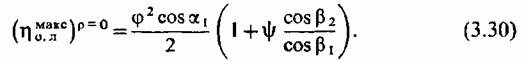
 может быть получена непосредственно путем подсчета потерь в решетках и потери с выходной скоростью при разных и/сф и при соблюдении принятых ранее допущений. Выражая потери в долях располагаемой энергии и вычитая сумму потерь из единицы, мы должны получить ту же кривую для КПД ступени, что и по формуле (3.28). может быть получена непосредственно путем подсчета потерь в решетках и потери с выходной скоростью при разных и/сф и при соблюдении принятых ранее допущений. Выражая потери в долях располагаемой энергии и вычитая сумму потерь из единицы, мы должны получить ту же кривую для КПД ступени, что и по формуле (3.28).
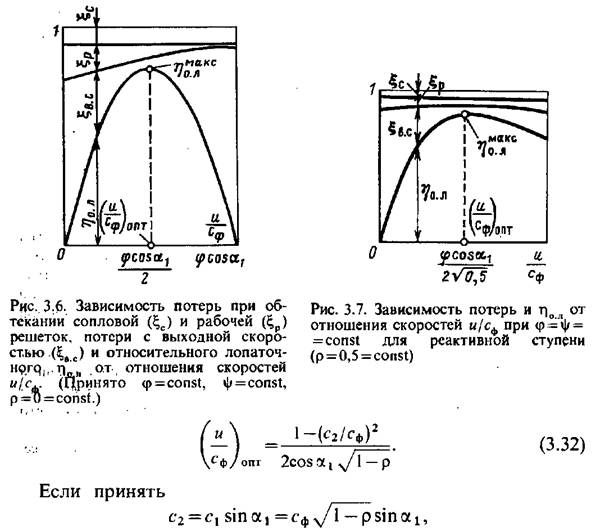
Проведенный таким образом расчет позволяет построить кривые изменения отдельных потерь в зависимости от и/сф (рис. 3.6).
Эти кривые показывают, что наиболее сильно от м/с зависят потери с выходной скоростью и что максимум КПД получается примерно при том отношении скоростей и/сф, где потери с выходной скоростью имеют наименьшую величину.
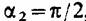 , то можно вывести формулу для , то можно вывести формулу для
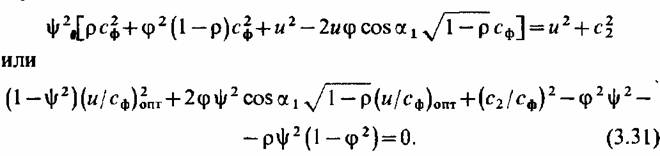 = н2 + С2> и тогда = н2 + С2> и тогда
 , получим выражение для оптимального отношения скоростей: , получим выражение для оптимального отношения скоростей:
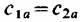 , то , то
получим

Таким образом, оказывается, что оптимальное отношение
 Из (3.29) Из (3.29)

.При сравнении ступеней с р = 0 и р = 0,5 по формуле (3.33) видно, что во втором случае оптимальное отношение скоростей в у/2 раз больше, а при_ той же окружной скорости и оптимальный теплоперепад Я0 в 2 раза меньше. Зависимость потерь и г|о.л для ступени с р = 0,5 показана на рис. 3.7.
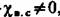 то оптимальное отношение скоростей будет выше, а кривая г|0л =/(и/с^) окажется более пологой. то оптимальное отношение скоростей будет выше, а кривая г|0л =/(и/с^) окажется более пологой.
Следует отметить, что величина Хв.с зависит от угла входа в последующую сопловую решетку. Обычно эта решетка проектируется под углом входа а0 = 90с, т.е. угол выхода из предыдущей ступени а2 = 90°. В этом случае потери при обтекании сопловой решетки будут минимальными. Иногда для работы ступени при малом ы/сф<(ы/Гф)опт и некоторого повышения ее КПД для этого режима сопловую решетку последующей ступени профилируют для угла входа а0<90 Однако при этом из-за большого поворота потока в решетке потери энергии и особенно концевые потери будут выше, чем в обычной решетке, спроектированной для угла входа а2 = 90° и обтекаемой под таким углом.
Таким образом, с учетом изменения величины %я-с в зависимости от угла а2 оказывается, что наивысший КПД с частичным использованием выходной скорости в последующей ступени достигается при у.2^9& что обеспечивается при отношении скоростей, примерно равном тому, что подсчитывается по (3.33).
Случай, когда ступень проектируется с я2>^- рассматривается ниже, в § 4.5.
|