Паровые турбины. Часть 1Расчет ступени с учетом изменения параметров потока по радиусу
Основные уравнения и методы расчета
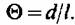 Практически расчеты, основанные на постоян- Практически расчеты, основанные на постоян-

При большой веерности предположение о плоскопараллельном течении в решетках турбинной ступени становится недостаточно оправданным, и такой расчет ступени при ее проектировании может привести к заметному снижению КПД.
 , то в данной пространственной задаче он разлагается на три составляющие: , то в данной пространственной задаче он разлагается на три составляющие:

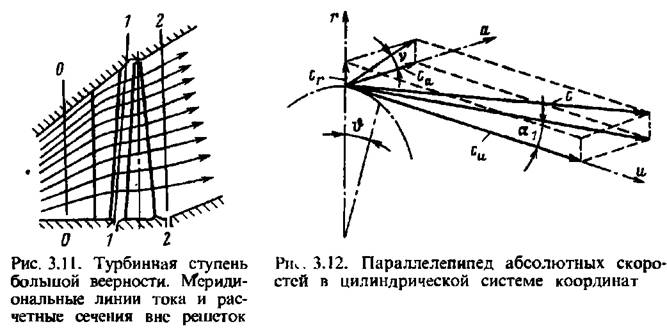
связанные между собой через угол потока на цилиндрической поверхности айв меридиональной плоскости V (рис. 3.12):

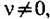 то кроме того то кроме того
на них действуют дополнительные силы от ускорения, возникающего при движении пара вдоль иецилиндрической поверхности тока. В радиальном направлении всем этим силам противодействует градиент давления </р/с1г, в результате чего оказывается, что по радиусу (высоте) ступени давление пара не одинаково.
Наибольшие изменения давления по радиусу обычно отвечают сечению /--/ (рис. 3.11), т.е. зазору между сопловой и рабочей решетками, так как в этом сечении поток наиболее закручен: здесь и наименьшие углы ос направления абсолютной скорости, и наибольшие скорости с, т. е. наибольшие значения си. Недостаточность информации о реальном характере потока, детальном изменении его характеристик по радиусу и по оси я, ограниченные пока возможности вычислительной техники затрудняют для сложных условий течения вязкой, сжимаемой жидкости, иногда с М^1 в паротурбинных ступенях большой веерности достаточно корректно поставить и точно решить задачу расчета так называемого пространственного потока.
Однако имеется много в той или иной мере приближенных методов расчета, также достаточно сложных, они позволяют качественно, а иногда и близко к данным экспериментального исследования количественно выявить влияние тех или иных факторов на характеристики потока в ступенях большой веерное™, произвести расчет ступени при переменных по радиусу параметрах потока.
Ниже представлена схема одного из таких методов, которая показывает влияние основных факторов на изменение параметров потока по радиусу, в частности в зазоре между решетками ступени.
Используя цилиндрическую систему координат (рис. 3.12), запишем для установившегося движения:
уравнения количества движения (уравнения Эйлера) [12, 43]

и уравнение неразрывноети

Здесь и далее Ра, Ри и /- составляющие внешних сил (например, от лопаток, гравитационных, мапштогидродинамических и т. д.). В последующих уравнениях, приводимых здесь выводе и анализе этими силами пренебрегаем.
Для относительного движения в рабочей решетке уравнения количества движения примут вид

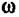 —• угловая скорость. —• угловая скорость.
 неразрывности запишется так: неразрывности запишется так:
Из этих уравнений следует, что в общем случае давление пара меняется не только в осевом направлении а и по шагу решетки г (по углу V), но также и по радиусу г. Изменение давления пара по радиусу описывается уравнением количества движения в проекции на ось г, т. е. уравнением (3.47), в котором первый член в правой части с*/г характеризует влияние центробежных сил, а остальные члены — влияние радиального ускорения.
Уравнение количества движения в проекции на ось г называется уравнением радиального равновесия. В форме (3.47) оно учитывает и радиальное ускорение. Как и при расчете ступени по среднему диаметру, при расчете пространственного потока могут ставиться обратная и прямая задачи, т. е. определяются или все размеры решеток (проектируется ступень), или все параметры при заданных размерах ступени (см. гл. 7).
При проектировании ступени большой веерности обратная задача обычно решается в упрощенной постановке, т. е. при заданных условиях определяются вне решеток параметры потока и векторы скорости, переменные по радиусу, а затем для каждого радиуса подбираются (или профилируются) решетки профилей. Таким образом, расчет ведется для трех сечений ступени: 0—0, 1—1 и 2—2 (рис. 3.11).
В настоящее время расчеты пространственного потока для кольцевых турбинных решеток и ступени в целом проводятся, как правило, упрощенно--для осесимметричного потока, т.е. в предположении д/ду = 0. При этом упрощенные (без членов с д/ду) уравнения количества движения не учитывают массовых сил воздействия лопаток на ноток />, что справедливо для пространства вне решеток, в частности для сечений 0—О, 1—1, 2—2 (рис. 3.11).
Для сопловой решетки используются уравнения (3.47), (3.49) и (3.50). К ним добавляются уравнение процесса, например уравнение изоэнтропы

и уравнение сохранения энергии, записанное для линии тока,
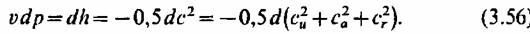
 Далее из предварительного расчета ступени, проведенного по среднему диаметру (§ 3.3), должны быть получены все меридиональные размеры ступени и известны параметры пара на входе в ступень, давление между решетками и на выходе из ступени на среднем радиусе (рис. 3.1). Далее из предварительного расчета ступени, проведенного по среднему диаметру (§ 3.3), должны быть получены все меридиональные размеры ступени и известны параметры пара на входе в ступень, давление между решетками и на выходе из ступени на среднем радиусе (рис. 3.1).
Кроме перечисленных условий решение задачи требует еще замыкающего соотношения, называемого законом закрутки. Для определения параметров потока в сечении 1 — / необходимо задаться законом закрутки сопловой решетки, а для параметров в сечении 2—2 — законом закрутки рабочей решетки. Эти законы закрутки рассматриваются ниже.
Для расчета ступени и подбора для нее решеток важно знать изменение скоростей потока.
Преобразуем уравнения так, чтобы получить зависимости дс/дг и дс/да. Подставив в (3.47) выражение (3.46) и помня, что

Разделив (3.60) на (3.61) и учтя, что (1р1<1(^) равно квадрату скорости распространения звука, а также обозначив через Ма отношение осевой скорости са к скорости звука, получим
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение

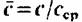 но радиусу: но радиусу:
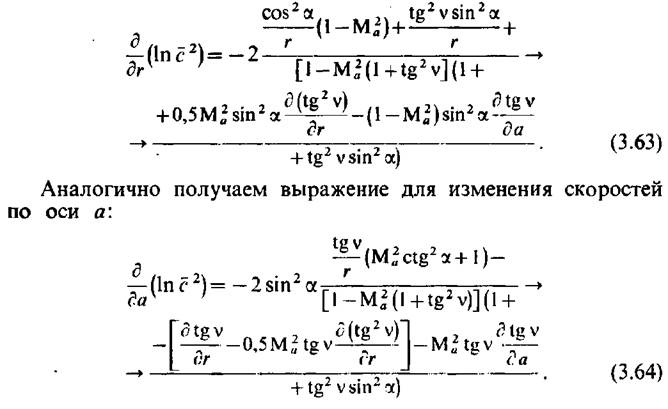
Эти уравнения решаются на ЭВМ. Как первое приближение иногда задаются уравнениями меридиональных линий тока, требующих уточнения по известным (или полученным по предварительному расчету) размерам
решеток. В ряде случаев для численного решения основных уравнений (3.47) (3.50) или (3.51) (3.54) они преобразуются к такой форме, когда в итоговых выражениях отсутствуют производные в осевом направлении. вмесю которых появляется кривизна меридиональных линий гока К^, в общем случае переменная и но радиусу, и по осевому направлению [45]. например
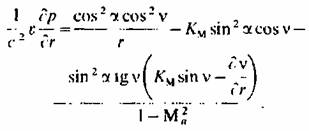
В последнее время появились методы расчета полноеыо фсхмсрпого траисзв>-ково! о потока в турбинной с гунсни, хотя при решении делаезся ряд немаловажных допущений. Эти методы позволяют ;ия заданною режима определить сетку мерили-

опальных линий тока, найти для разных сечений изотахи (линии постоянной скорости X) или изобары.
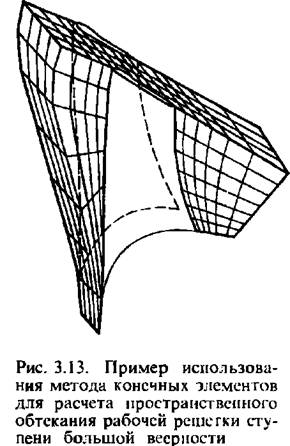
Для иллюстрации на рис. 3.13 показана сетка линий тока применительно к одной из последних лопаток мощной паровой турбины, полученная использованием численного метода конечных элементов, а на рис. 3.14 даны результаты расчета невязкой жидкости в последней ступени тихоходной турбины большой мощности. Эти результаты получены на основе применения принципа установления и конечно-разностной схемы решения системы нестационарных уравнений, описывающих пространственное течение в ступени.

На основе уравнения (3.63) проанализируем влияние ряда факторов на распределение давления р, и скорости си в зазоре между решетками. Для этого сначала рассмотрим некоторые частные случаи.
1. В частном случае цилиндрических поверхностей тока
(рис. 3.15,а), т.е. при 1§у = 0, получаем простое уравнение

 записывается в виде записывается в виде
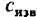
Как видно из (3.66), от корня к периферии скорость потока уменьшается, причем тем больше, чем меньше угол а, т. е. чем больше закрутка потока.
 (рис. 3.15,6) скорость потока от корня к периферии уменьшается сильнее, чем в цилиндрической схеме (случай 1). Влияние конусности потока оказывается тем большим, чем больше число Мв. (рис. 3.15,6) скорость потока от корня к периферии уменьшается сильнее, чем в цилиндрической схеме (случай 1). Влияние конусности потока оказывается тем большим, чем больше число Мв.
В решетке с коническими поверхностями тока и увеличением абсолютного угла наклона их от корня к периферии (рис. 3.15, в) скорость падает в еще большей степени (например, ступень с корневым цилиндрическим и периферийным коническим обводами, рис. 3.11).
Обратная картина будет наблюдаться для решетки, изображенной на рис. 3.15, г.

 всего па несколько процентов [34]. всего па несколько процентов [34].
4. В случае кривизны меридиональных линий тока на участке с выпуклостью их к оси решетки (рис. 3.15,(3) уменьшение скорости к периферии замедляется (рис. 3.16), и, наоборот, увеличивается разница в скоростях при вогнутой к оси решетки форме меридиональной линии тока (рис. 3.15,^).
 и числа М1(=/, (г) для сопловой и числа М1(=/, (г) для сопловой
 , давления в зазоре р^—р{г) и числа , давления в зазоре р^—р{г) и числа
М 2( =/2 (г) для раоочей решетки, в-третьих — от изменения площади канала решеток по осям г и а.
Как первое приближение, особенно для ступеней с цилиндрическими меридиональными обводами, может служить гипотеза о цилиндрических поверхностях тока. В этом случае решение задачи о распределении параметров потока по радиусу может быть получено как из общих уравнений [для сопловой решетки из (3.66)], так и более простым путем. В частности, если для элементарной массы пара в зазоре между решетками найти центробежную силу, то из условия радиального равновесия этой частицы получим
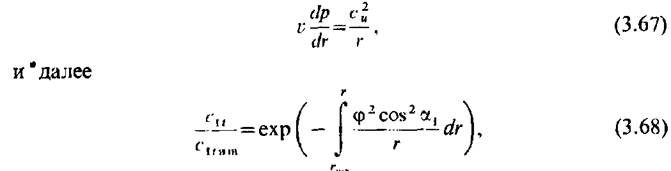
где индекс изв относится к радиусу, где известны все параметры потока.
Выражение (3.68) отличается от (3.66) введением коэффициента скорости ф, так как при выводе в отличие от (3.63) не использовалось уравнение изоэнтропийного процесса (3.55).
Выражение (3.67) часто называют упрощенным уравнением радиального равновесия, и оно может быть записано для каждого из сечений вне решеток, т. е. для сечений 0—0, 1-1 и 2--2 (рис. 3.11):
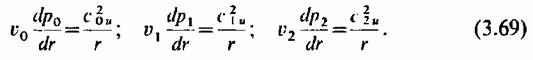
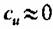 и, и,
следовательно, при постоянстве по радиусу температуры пара перед сопловой решеткой располагаемый теплоперепад ступени не меняется по радиусу, получаем формулу для определения изменения по радиусу степени реактивности:
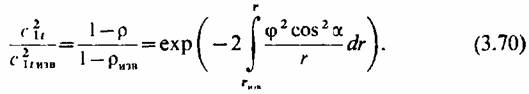

Первая из этих зависимостей является упомянутым выше замыкающим соотношением, называемым законом закрут-к и сопловой решетки.
|