Технология переработки нефти и газа. Часть2Расчет критических параметров и молярных масс углеводородных смесей.
Раздел подготовлен на основании статьи Жукова Н.П, Быченка В.И., Черепинникова И.А., Кузьмина С.Н. К расчету критических параметров нефтепродуктов. /Химия и технология топлив и масел, №4, 1993. – С. 29-32.
П рименение новых технологий и рабочих веществ для интенсификации процессов переработки нефти требует внедрения эффективных методов рас-чета аппаратуры, в том числе теплофизических характеристик (ТФХ) веществ, особенно жидких, поскольку теория их строения является преимущественно качественной.
Экспериментальные методы определения ТФХ ввиду их дороговизны и длительности малоэффективны. Поэтому в инженерной практике предпочте-ние отдают приближенным методам расчета обобщающих ТФХ. Среди них наиболее распространены методы, использующие критические параметры. Применение последних в прямой форме и в виде относительных переменных в теории соответственных состояний позволяет приближенно рассчитать та-кие физические характеристики, как объем, энтальпия, теплопроводность, те-плота парообразования, поверхностное натяжение, коэффициент объемного расширения и др. Для сложных смесей, к которым относятся нефтепродукты, критические параметры, строго говоря, являются псевдокритическими. Одна-ко, следуя терминам, общепринятым в литературе по нефтепереработке и нефтехимии, будем называть их критическими.
Рассмотрим методы расчета критических температуры Ткр и давления ркр для нефтепродуктов по минимальному числу исходных данных. В качестве таких данных используем температуру кипения и относительную плотность r42 0 жидкого нефтепродукта, которая была принята ранее в СССР в качестве стандартной характеристики.
Определение критической температуры. Для большой группы однокомпо-нентных жидкостей (включая органические) получен ряд расчетных формул. Некоторые из них приведены ниже.
Для н-парафиновых углеводородов (от метана до н-пентана включительно) применяют уравнение Гульдберга-Гюи:
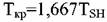 температура кипения, К. температура кипения, К.
Для низкокипящих (ТSH<235К) соединений и простых веществ рекоменду-ют формулу Мейсснера-Реддинга:
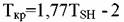 с ТSH=235-600К используют уравнение: с ТSH=235-600К используют уравнение:
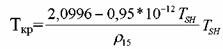 : :
где r15 - плотность жидкости при 150С, кг/м3.
Кроме того, А.М. Мамедовым предложены зависимости: для н-парафиновых углеводородов
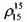 - плотность жидкости при150С, отнесенная к плотности воды при 150С. - плотность жидкости при150С, отнесенная к плотности воды при 150С.
При известных значениях плотности r1 и r2 органической жидкости, соот-ветствующих температурам Т1 и Т2, критическую температуру кипения Ткр приближенно можно найти по формуле Л.П. Филиппова:
где
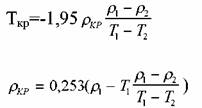 и неполярных углеводородов используют формулу Нокая: и неполярных углеводородов используют формулу Нокая:
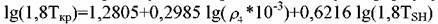 жидкости при 40С (допустимо использование плотности при 200С), кг/м3. жидкости при 40С (допустимо использование плотности при 200С), кг/м3.
Для эфиров, ассоциированных ароматических соединений, полярных угле-водородов, неполярных органических соединений и неорганических веществ предназначена Формула Чен-Ху:
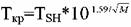 разработан только для углеводородов. Так, для жидко-стей с ТSH>235K предложено использовать метод Мейсснера-Реддинга: разработан только для углеводородов. Так, для жидко-стей с ТSH>235K предложено использовать метод Мейсснера-Реддинга:
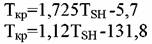 и Тодоса: и Тодоса:
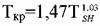 выражение Ткр для углеводородов: выражение Ткр для углеводородов:
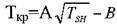 , ,
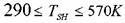 и ацетиленовых углеводородов А=40 и В=230 при . Для алифатических углеводородов можно использовать формулы: и ацетиленовых углеводородов А=40 и В=230 при . Для алифатических углеводородов можно использовать формулы:
 , зависящие от давления насыщенных паров; a, b - по-стоянные уравнения Ван-дер-Ваальса; R - универсальная газовая постоянная, Дж/(кмольК). , зависящие от давления насыщенных паров; a, b - по-стоянные уравнения Ван-дер-Ваальса; R - универсальная газовая постоянная, Дж/(кмольК).
Для н-парафиновых углеводородов Ткр можно выразить через молярную массу М:
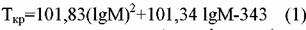 соединений и нафтенов (не содержащих галогены и се-ру) предложена формула: соединений и нафтенов (не содержащих галогены и се-ру) предложена формула:
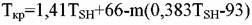 числа атомов углерода, не входящих в кольцо, к их общему числу в молекуле. числа атомов углерода, не входящих в кольцо, к их общему числу в молекуле.
Разработаны также методы на основе суммирования атомных и структур-ных составляющих. Они предусматривают использование нормальной темпе-ратуры кипения и химической бурутто-формулы вещества в качестве исход-ных данных. Чаще других применяют зависимости Гульдберга, Риделя и Ли-дерсена.
Расчет критической температуры кипения смесей неопределенного состава осложняется, и для них применяют приближенные зависимости. Из смесей за-данного состава следует выделить бинарные, для которых по сравнительно громоздким формулам можно получить более точные результаты. При из-вестных критических температурах кипения компонентов критическую тем-пературу кипения смеси можно приближенно рассчитать по зависимости Кэя, основанной на правиле аддитивности:
 доля i-го компонента в смеси. доля i-го компонента в смеси.
Для смесей неопределенного состава формула (2) неприменима. В этом случае Ткр отыскивают по различным эмпирическим зависимостям. Для угле-водородов и топливных фракций (бензиновых, керосиновых, газойлевых и др.) можно использовать формулу Итона и Портера:
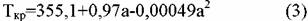 температура; температура;
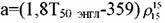 - индивидуальный коэффициент, характеризующий фи-зические свойства нефтепродукта; Т50энгл - температура выкипания 50% объе-ма нефтепродукта по ГОСТ 2177-82, К. - индивидуальный коэффициент, характеризующий фи-зические свойства нефтепродукта; Т50энгл - температура выкипания 50% объе-ма нефтепродукта по ГОСТ 2177-82, К.
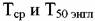 . .
С термодинамической точки зрения иногда удобнее принимать за темпера-туру кипения величину, физический смысл которой раскрывается ниже.
Для моторных топлив предлагается формула
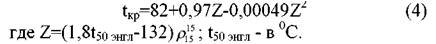
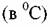 неф- неф-
тяных фракций в инженерной практике применяется формула
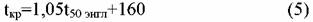 упрощенная формула Паркера и Макки для вычисления Ткр нефтяных фракций (в шкале Кельвина): упрощенная формула Паркера и Макки для вычисления Ткр нефтяных фракций (в шкале Кельвина):
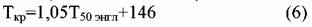 приведенные для расчета критической температуры смесей выражения, можно отметить, что для них не указываются пределы примени-мости и не приводятся средние и максимальные погрешности расчета. Кроме того, ими невозможно пользоваться в отсутствие сведений о специфических средних температурах кипения смесей. С увеличением числа новых рабочих веществ, физические свойства которых определяются экспериментально по сокращенной программе, возникает необходимость в расчете Ткр смесей по другим аргументам. приведенные для расчета критической температуры смесей выражения, можно отметить, что для них не указываются пределы примени-мости и не приводятся средние и максимальные погрешности расчета. Кроме того, ими невозможно пользоваться в отсутствие сведений о специфических средних температурах кипения смесей. С увеличением числа новых рабочих веществ, физические свойства которых определяются экспериментально по сокращенной программе, возникает необходимость в расчете Ткр смесей по другим аргументам.
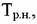 при которой жидкости находятся в равновесии с паром, имеющим при которой жидкости находятся в равновесии с паром, имеющим
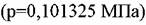 . .
Температуру Тр.н. используют и для расчета ТФХ веществ. По физическому смыслу она является аналогом нормальной температуры кипения однокомпо-нентных жидкостей. Таким образом, для смесей неопределенного состава в отдельных случаях необходима приближенная оценка свойств по минималь-ному числу исходных данных, включающих и Тр.н..
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
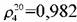 - -
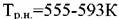 крити- крити-
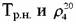 . .
В результате математической обработки методом наименьших квадратов получена следующая зависимость :
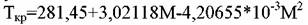 по температуре Тр.н. с помощью уравнения (7). по температуре Тр.н. с помощью уравнения (7).
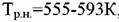 , ,
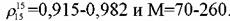 молярной массы молярной массы
Наиболее точно молярную массу смесей можно определить аналитически-ми методами: криоскопическим, эбулиоскопическим и, реже, осмометриче-ским. Приближенно ее можно рассчитать следующими методами: для смеси известного состава - по мольной доле и молярной массе компонентов с ис-пользованием правил аддитивности; для таких смесей, как нефть, нефтяные фракции и нефтепродукты, - по уравнениям Б.М. Воинова. Последние имеют вид:
для н-парафиновых углеводородов и узких нефтяных фракций парафинового основания:
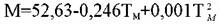 (7) (7)
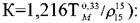
 ароматических углеводородов ароматических углеводородов
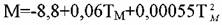 (9) Для бензиновых фракций рекомендована формула (9) Для бензиновых фракций рекомендована формула
 можно использовать также приближенную формулу Крэга можно использовать также приближенную формулу Крэга
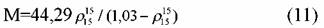 показывают, что формула Крэга не всегда дает удовлетво-рительные результаты. показывают, что формула Крэга не всегда дает удовлетво-рительные результаты.
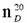 , находим , находим
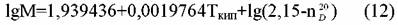 неопределенного состава рекомендовано уравнение: неопределенного состава рекомендовано уравнение:
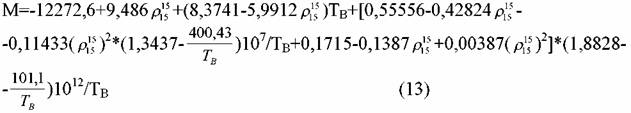 ТВ - нормальная температура кипения, полученная как средняя точка тем-пературного диапазона кипения при нормальном атмосферном давлении. Приближенно рассчитать М можно по уравнениям Кистяковского: ТВ - нормальная температура кипения, полученная как средняя точка тем-пературного диапазона кипения при нормальном атмосферном давлении. Приближенно рассчитать М можно по уравнениям Кистяковского:
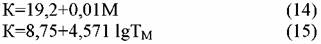 пропорциональности к правилу Трутона. пропорциональности к правилу Трутона.
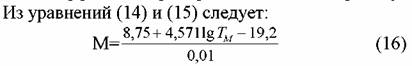 критического давления. Большая часть формул для расчета критического давления получена для однокомпонентных жидкостей. Для сме-сей известного состава критическое давление можно вычислить по формуле критического давления. Большая часть формул для расчета критического давления получена для однокомпонентных жидкостей. Для сме-сей известного состава критическое давление можно вычислить по формуле
 Льюиса: Льюиса:
где ркр - в Па; K - коэффициент, определяемый в зависимости от химического состава фракций или по формулам.
Для углеводородов (кроме нафтеновых и ароматических) можно использо-вать приближенную формулу Герцога:
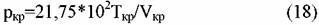 объем вещества в критической точке, м3/моль. объем вещества в критической точке, м3/моль.
Для н-парафиновых углеводородов применимо уравнение Тиличеева и Та-тевского:
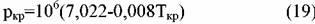 (кроме нафтеновых и ароматических) с нормальной температурой кипения ТSH=236-600 К рекомендуют уравнение Мейсснера: (кроме нафтеновых и ароматических) с нормальной температурой кипения ТSH=236-600 К рекомендуют уравнение Мейсснера:
 углеводородов можно использовать формулу углеводородов можно использовать формулу
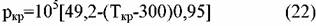 С2-С5 приближенно справедливо уравнение Фроста С2-С5 приближенно справедливо уравнение Фроста
|