Вязкость смесей и растворов А Зависимость вязкости смесей от соотношения компонентов

Нефтепродукты представляют собой смеси индивидуальных соединений. Их вязкость зависит от свойств, концентрации и взаимодействия компонентов смеси.

В развитии учения о вязкости смесей жидкостей выдающуюся роль сыграли фундаментальные исследования школы Н. С. Кур-накова .

Н. С. Курнаков и его сотрудники делят кривые вязкость — концентрация двухкомпонентных смесей при постоянной температуре (изотермы вязкости) на следующие четыре типа (фиг. 65).

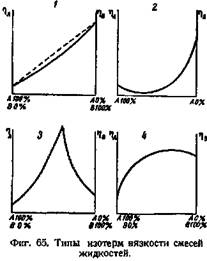
Непрерывные кривые, близкие к прямой, соединяющей значения вязкости исходных компонентов (кривая /, фиг. 65). Они характерны для смесей нормальных или почти нормальных жидкостей, между которыми нет химического взаимодействия. У реальных смесей кривые обычно несколько выгнуты по направлению к оси абсцисс.

Кривые с минимумом вязкости (кривая 2, фиг. 65). Они возникают при диссоциации ассоциированных молекул одного из компонентов смеси под влиянием другого.

Кривые с отчетливым максимумом вязкости (кривая 3, фиг. 65). Они отвечают смесям, в которых при оп редел енном соотношении компонентов образуются не-диссоциированные соединения. Такие системы называют рациональными или сингулярными. Изотермы вязкости состоят как бы из двух ветвей, пересекающихся в точке максимума, называемой сингулярной точкой.

Кривые с размытым максимумом (кривая 4, фиг. 65), характеризующие смеси, в которых возникают диссоциирующиеся химические соединения. Такие системы называются иррациональными.

Детальная классификация рациональных и иррациональных систем разработана Н. А. Трифоновым . Подробное ее обсуждение и критику можно найти в монографии В. Я. Аносова и С. А. Погодина . Интересный тип 5-образных изотерм вязкости изучен М. И. Усановичем . В упомянутой монографии В. Я. Аносова и С. А. Погодина и в статье Н. К. Воскресенской, М. И. Равича и Э. Б. Штерниной рассмотрены пути использования вискозиметрии для физико-химического анализа жидких систем.

Как правило, смеси жидких индивидуальных углеводородов и других неполярных составных частей нефти, а также жидких нефтепродуктов при комнатной и более высокой температуре дают кривые первого типа. По мере повышения температуры кривая, соединяющая точки, отвечающие вязкости исходных компонентов, спрямляется, а со снижением температуры прогиб кривой возрастает. При достаточно низких температурах прогиб кривой настолько увеличивается, что кривые следует относить ко второму типу. Изменение типа смеси связано с нарастанием ассоциации вязкого компонента смеси при низкой температуре . Разбавление ассоциированного компонента приводит к его частичной диссоциации.

Концентрационная зависимость вязкости растворов твердых нефтепродуктов в жидких также относится к первому или, реже, ко второму типу. Однако в связи с застыванием или кристаллизацией таких растворов они могут существовать в жидком и гомогенном состоянии только до не слишком высоких концентраций, соответственно с чем могут быть получены только начальные участки кривых вязкость—концентрация.

или в логарифмической форме

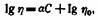
пригоден для вычисления вязкости смесей масел с бензинами и растворов полиизобутиленов и некоторых других высокополимеров в минеральных маслах. К аналогичным выводам пришел Г. В. Виноградов.

Нами совместно с Н. Г. Пучковым было обнаружено, что для растворов полиизобутиленов в маслах постоянная уравнения (IV, 29) или точнее варианта, в котором динамическая вязкость заменена кинематической, представляет собой линейную функцию молекулярного веса полимера

где ft и у — постоянные величины; М—молекулярный вес.

Комбинируя это уравнение для а с уравнением (IV, 30) и переходя к относительной кинематической вязкости, можно притти к уравнению

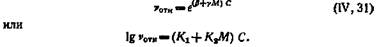
Оказалось, что величина у в некоторых пределах обратно пропорциональна вязкости масла-растворителя.

Закономерности, полученные М. М. Кусаковым и автором, соблюдаются для растворов высокомолекулярных соединений до 3—4%, а для растворов соединений с молекулярным весом ниже 10—15 . 103 до 10—15% и больше. В последнее время нами было показано , что формула (IV, 29) позволяет вычислять вязкость смесей в очень широком интервале соотношений фракций. Это дает основание предполагать, что после дальнейшей проверки она найдет широкое применение для вычисления вязкости смесей нефтепродуктов.

Неоднократно делались попытки вывести формулы для расчета вязкости смесей, исходя из уравнения А. И. Бачинского. Для идеальных бинарных смесей двух жидкостей Л и Б Г. П. Лучин-ский пришел к следующему выражению:

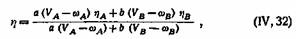
где а и Ь — весовые доли жидкостей А и В: VA и VB — удельные объемы этих жидкостей; со—предельный объем. Эта формула дала хорошее совпадение вычисленных данных с экспериментальными для смесей маловязких жидкостей (бензол с толуолом, хлороформ с бензолом, сероуглерод с толуолом).

Г. П. Лучинским была также предложена формула, охватывающая все типы изотерм вязкости, в том числе неидеальных:

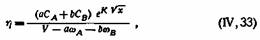
где х—молекулярная доля компонента, содержащегося в смеси в меньшем количестве; К —константа, равная для многих смесей 0,15. Формула (IV, 33) пока еще недостаточно проверена