Построение высоконадежных системПостроение грубых моделей для оценки сверху и снизу
На примере метода минимальных путей и минимальных сечений. Одним из важных приемов при ориентировочной оценке вероятностных характеристик сложных систем, точные математические модели которых неоправданно громоздки, является построение существенно более простых приближенных моделей, позволяющих оценивать истинную модель сверху и снизу. Мы приведем пример, который хорошо иллюстрирует применение этого приема к одной из интересных и важных в практическом отношении задач.
Большинство реальных сетей связи, обеспечивающих информационный обмен между большим числом территориально разнесенных пунктов, имеет очень сложную структуру. Связь между отдельными пунктами информационной сети может осуществляться по многим возможным путям, включая транзит по целому ряду пунктов. Несколько идеализируя характер работы сети связи, будем считать, что возможны любые транзиты информации. (Как будет показано позже, это не очень сильно искажает реальную картину, так как вносимые за счет такой идеализации длинные пути слабо влияют на основные показатели надежности.)
Строгий анализ сети связи с произвольной структурой, по существу, возможен лишь методом прямого перебора. Каждое состояние анализируется в соответствии с выбранным критерием работоспособности, что само по себе достаточно сложно. К тому же даже относительно простые реальные системы с числом элементов (каналов связи и пунктов) порядка 30—40 приводят к необходимости перебора миллионов состояний.
Рассмотрим произвольную сложную сеть связи и оценим одну из важных характеристик — вероятность связи двух фиксированных пунктов.
Введем в рассмотрение так называемую структурную функцию
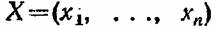 — вектор, компонентами которого являются индикаторы работоспособности отдельных каналов связи: — вектор, компонентами которого являются индикаторы работоспособности отдельных каналов связи:

(Для упрощения будем считать, что надежность пунктов в информационной сети идеальна.)
Можно показать, что любая структурная функция для сети выражается эквивалентным образом через так называемые минимальные пути и минимальные сечения [2].
Путем в сети естественно назвать последовательность каналов связи, которые позволяют передать некоторую информацию из начального пункта в конечный , а сечением — такую совокупность каналов связи, удаление которых из сети приводит к нарушению такой передачи информации. (Здесь и далее мы предполагаем, что при нашей постановке задачи—передача информации из одного пункта в другой — наша сеть связи может рассматриваться как некоторый двухполюсник.)
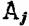 сети свяжем логическую функцию сети свяжем логическую функцию
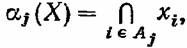
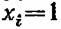
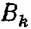 мы также поставим в соответствие логическую функцию мы также поставим в соответствие логическую функцию
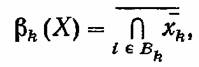
которая принимает значение 0, если все элементы, принадлежащие минимальному сечению, неисправны, и 1 в противном случае, т. е. если хотя бы один из этих элементов функционирует нормально.
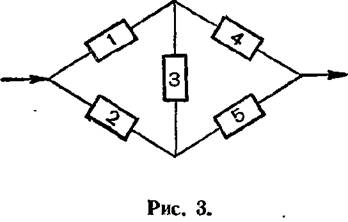
Понятно, что сеть общего вида может иметь несколько минимальных путей. Так, для простейшей сети, структура которой не может быть представлена в виде чисто параллельного или чисто последовательного соединения (рис. 3), минимальными путями будут следующие подмножества элементов: (1, 4), (1, 3, 5), (2, 5), (2, 3, 4), а минимальными сечениями—подмножества : (1, 2), (4, 5), (1, 3, 5), (4, 3, 2).
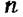 минимальных путей, каждый из которых состоит всего из одного элемента. минимальных путей, каждый из которых состоит всего из одного элемента.
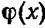 произвольной сети может быть выражена либо через структурные функции всех г своих минимальных путей, либо через структурные функции всех 5 своих минимальных сечений: произвольной сети может быть выражена либо через структурные функции всех г своих минимальных путей, либо через структурные функции всех 5 своих минимальных сечений:
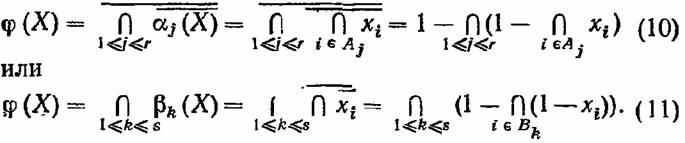
Оба эти выражения имеют простой содержательный смысл. Первое из них означает, что в сети для связи входа с выходом должен существовать хотя бы один из путей, а второе означает, что для связи входа с выходом в сети каждое из минимальных сечений должно содержать хотя бы один работоспособный элемент, т. е. в сети не должно существовать ни одного размыкающего ее сечения.
Иными словами, любую структуру можно представить в виде параллельного соединения минимальных путей либо в виде последовательного соединения минимальных сечений.
Представимость структурной функции системы в таком виде поясним на примере мостиковой схемы, приведенной ранее:
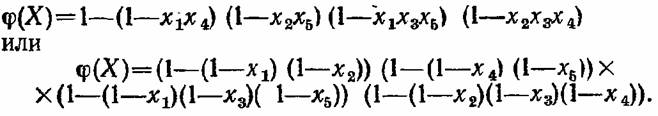
Представление произвольной структуры в виде параллельного или последовательного соединений некоторых цепочек является в большой степени условным. Действительно, нетрудно заметить, что в произвольной структуре (например, в мостиковой схеме) одни и те же элементы могут входить в различные минимальные пути и сечения.. Иначе говоря, некоторые из параллельно соединенных минимальных путей (или некоторые последовательно соединенные минимальные сечения) оказываются зависимыми, что не позволяет использовать хорошо разработанный математический аппарат для оценки надежности таких соединений, построенный в предложении независимости отдельных элементов системы . Например известно, что для последовательного соединения п независимых элементов вероятность безотказной работы по формуле
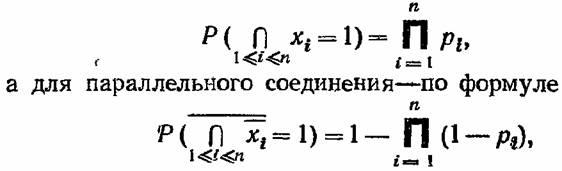
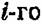
элемента соответствующей системы.
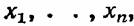 принимающих значения 1 и 0, справедливо условие принимающих значения 1 и 0, справедливо условие
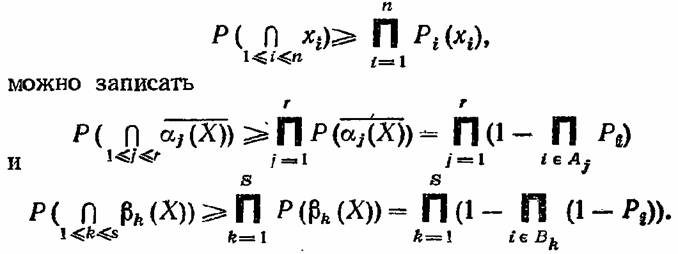
Используя эти неравенства и полученные ранее выражения для структурных функций, после несложных преобразований получаем, верхнюю и нижнюю оценку для вероятности безотказной работы системы с произвольной структурой

Таким образом, для приближенной оценки надежности системы со сложной структурой достаточно выявить минимальные пути и минимальные сечения. К тому же заметим, что практически оказывается необходимо находить из минимальных путей лишь самые короткие, а из минимальных сечений лишь самые тонкие, так как именно они оказывают наиболее существенное влияние на окончательный результат.
Итак, на ранней стадии проектирования сложной системы можно с успехом применять метод построения граничных моделей, оценки для которых являются гарантийными относительно трудноисследуемой реальной системы.
Задачи оптимизации структуры (на примере оптимального резервирования). Итак, система спроектирована, она может выполнять требуемые функции. Однако зачастую возникает вопрос о том, насколько надежно" будут эти функции выполняться.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
Имеется большое число методов повышения надежности, но одним из самых важных является резервирование. Обычно предполагается, что резервирование не затрагивает принципиальных решений: ни способа функционирования, ни структуры системы, ни характера ее составных частей Задача сводится к введению того или иного вида избыточности, основные типы которой мы рассмотрим ниже.
Прежде всего приведем очень краткую (а поэтому и далеко не полную) классификацию основных видов и способов резервирования.
При таком делении различают нагруженное и ненагружен ное резервирование. В первом случае резервные элементы находится в таких же режимах, что и основные рабочие элементы (этот тип резерва часто в инженерной практике называют горячим резервом). Во втором случае резервные элементы вступают в работу только лишь при отказе основных элементов, а до этого момента отказ их не может возникать ни по каким причинам (заметим, что этот тип резерва называется иногда холодным).
Если рассмотреть некий элемент и п параллельно включенных ему резервных элементов в нагруженном режиме, то случайное время жизни такой резервной системы будет равно
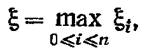

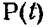 с нагруженным резервом можно записать выражение с нагруженным резервом можно записать выражение
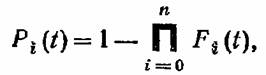
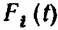 — распределение времени безотказной работы — распределение времени безотказной работы
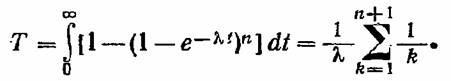
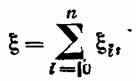 до отказа будет определяться как до отказа будет определяться как
так как первый резервный элемент вступит в работу лишь после отказа основного рабочего элемента, второй резервный элемент — лишь после отказа первого резервного и т. д.
Гипотеза о независимости отказов отдельных элементов в данном случае является более оправданной (хотя можно привести и противоположные примеры). Тогда вероятность безотказной работы системы, состоящей из п идентичных элементов, записывается в виде
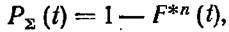
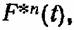 е. е.
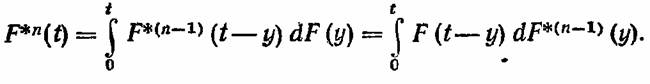
(Выражение для случая различных элементов записывается аналогично, но оно лишь более громоздко.)
Среднее время работы системы до отказа находится в данном случае элементарно даже для случая разных и даже зависимых элементов:
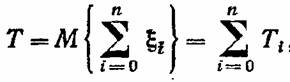
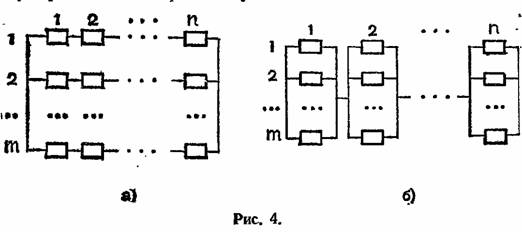 В первом случае целая цепочка последовательно соединенных элементов резервируется аналогичными цепочками. Во втором случае производится индивидуальное резервирование каждого из элементов (см. соответственно рис. 4, а и б). Выражения для вероятности безотказной работы системы в первом и во втором случаях равны соответственно В первом случае целая цепочка последовательно соединенных элементов резервируется аналогичными цепочками. Во втором случае производится индивидуальное резервирование каждого из элементов (см. соответственно рис. 4, а и б). Выражения для вероятности безотказной работы системы в первом и во втором случаях равны соответственно
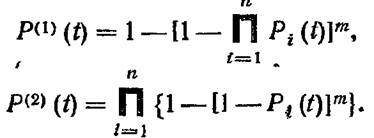
(Обозначения соответствуют рис. 4.)
Из приведенных формул видно, что в принципе раздельное резервирование всегда дает больший выигрыш по сравнению с общим. (Заметим ради справедливости, что при этих рассуждениях мы не учитывали тот факт, что для подключения резервных элементов нужны те или иные переключающие устройства, ненадежность которых в реальной ситуации может оказать решающее влияние на характеристики надежности всей системы и свести на нет все преимущества раздельного резервирования.)
Тот факт, что раздельное резервирование является более эффективным по сравнению с общим является достаточно очевидным и давно известным. Однако интересно отметить, что прямым образом доказать это утверждение на основании формул для вероятностей безотказной работы не прос-по , так как приходится иметь дело с очень громоздкими тромежуточными преобразованиями. Действительно, требуется доказать справедливость неравенства
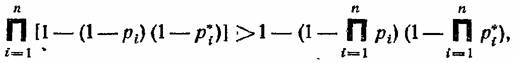
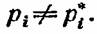
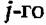 участка системы. Тогда, участка системы. Тогда,
учитывая, что время безотказной работы системы параллельно включенных элементов определяется максимумом из наработок отдельных элементов, а время безотказной работы системы последовательных элементов определяется минимумом соответствующих величин, можно записать для случайного времени безотказной работы рассматриваемых резервных систем:
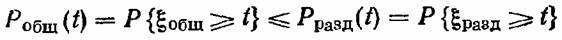
и то, что для средних времен безотказной работы также выполняется условие
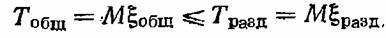
Наконец, резервирование бывает с восстановлением отказавших элементов и без восстановления. Системы без восстановления уже были нами описаны фактически при рассмотрении типов резерва по характеру нагрузки. Пример резервной системы с восстановлением был рассмотрен нами ранее в разделе, посвященном анализу системы, описываемой марковским процессом гибели и размножения.
Теперь после краткого изложения основных принципов резервирования перейдем к изложению так называемой задачи оптимального резервирования с учетом тех или иных технических или экономических ограничений.
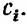 (Вообще говоря, затраты могут измеряться не только в стоимостных единицах, но и в единицах веса, объема, и т. п. Более того, может существовать одновременно несколько типов затрат, однако для простоты мы не будем рассматривать такие относительно сложные ситуации.) (Вообще говоря, затраты могут измеряться не только в стоимостных единицах, но и в единицах веса, объема, и т. п. Более того, может существовать одновременно несколько типов затрат, однако для простоты мы не будем рассматривать такие относительно сложные ситуации.)
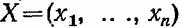 резервных элементов, то показатель надежности ее (например, вероятность безотказной работы или коэффициент готовности) может быть записан в виде резервных элементов, то показатель надежности ее (например, вероятность безотказной работы или коэффициент готовности) может быть записан в виде
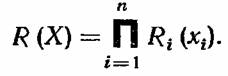
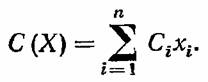
Простейшие и самые известные оптимальные задачи надежности связаны, по-видимому, именно с задачами резервирования. Можно сформулировать следующие прямую и обратную задачи условной оптимизации: 1) найти
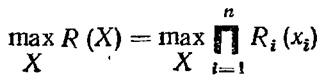
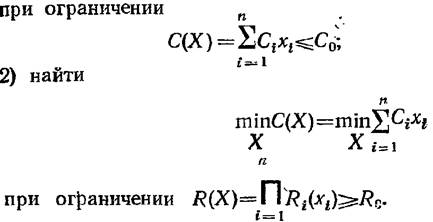
Существует несколько различных и в достаточной степени эффективных методов математического решения рассматриваемых задач оптимального резервирования (см., например, [10]).
Одним из простейших методов решения, дающих практически достаточно точное решение, а в ряде случаев и абсолютно точное решение, является метод - покоординатного наискорейшего спуска, который заключается в следующем.
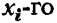 резервного элемента: резервного элемента:
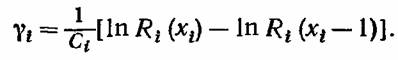
 является наибольшей. В результате такой процедуры может быть построен график зависимости показателя надежности системы 7? от затраченных средств С. является наибольшей. В результате такой процедуры может быть построен график зависимости показателя надежности системы 7? от затраченных средств С.
Следует заметить, что подобная процедура не дает возможности получить всегда строгое решение, однако нужда в чрезмерной строгости на практике и не возникает, так как статистические данные по надежности, используемые в расчетах, к сожалению, далеки от желаемой достоверности, да и задаваемые ограничения не являются столь категоричными на практике, как они выглядят в условиях математической задачи. Это позволяет считать что полученное при помощи такого алгоритма решение является вполне удовлетворительным для практических приложений. Более строгие решения могут быть получены, например, при помощи метода динамического программирования или путем использования какого-либо алгоритма целочисленного нелинейного программирования (вопрос о выборе алгоритма также выходит за рамки нашего рассмотрения)
|