Теория систем автоматического управленияВременные характеристики
Динамические свойства звена могут быть определены по его переходной функции и функции веса.
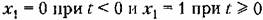 . Предполагается, что единица имеет ту же размерность, что и физическая величина на входе звена. . Предполагается, что единица имеет ту же размерность, что и физическая величина на входе звена.
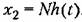
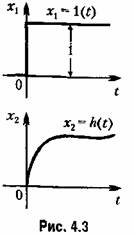
Ступенчатая функция представляет собой распространенный вид входного воздействия в автоматических системах. К такому виду сводятся мгновенное изменение нагрузки электрического генератора, мгновенное возрастание нагрузки на валу двигателя, мгновенный поворот командной оси следящей системы и т. п.
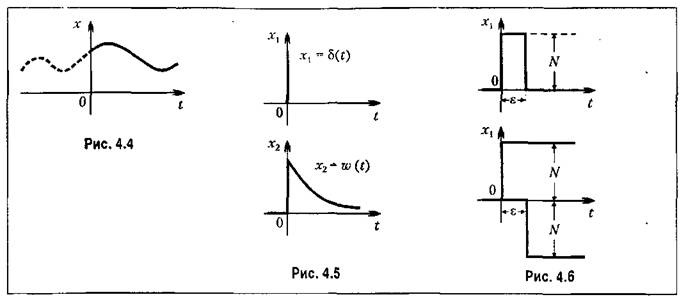
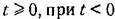 она обращается в нуль. Это иллюстрируется рис. 4.4. она обращается в нуль. Это иллюстрируется рис. 4.4.
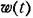 представляет собой реакцию звена на представляет собой реакцию звена на
единичную импульсную функцию, поданную на его вход (рис. 4.5).

 где она стремится к бесконечности. Основное свойство дельта-функции заключается в том, что где она стремится к бесконечности. Основное свойство дельта-функции заключается в том, что

т. е. она имеет единичную площадь.
 4.6). Такой импульс может быть 4.6). Такой импульс может быть
 прикладываемыми прикладываемыми
ко входу звена со сдвигом во времени е. Тогда выходная величина будет равна

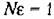 Помножив и поделив правую часть равенства (4.4) на е и перейдя к пределу, получим функцию веса Помножив и поделив правую часть равенства (4.4) на е и перейдя к пределу, получим функцию веса
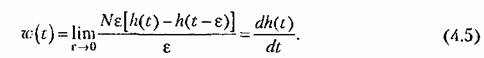
Таким образом, функция веса может быть получена дифференцированием но времени переходной функции.

Импульсная функция также представляет собой распространенный вид входного воздействия в автоматических системах. К такому виду, можно свести, например, кратковременный удар нагрузки на валу двигателя, кратковременный ток короткого замыкания генератора, отключаемый плавкими предохранителями, и т. п. В действительности реальные импульсные воздействия на автоматическую систему всегда будут конечными по величине и продолжительности. Однако в случае если их продолжительность весьма мала по сравнению с временем переходного процесса звена или автоматической системы, то с большой степенью точности реальный импульс может быть заменен дельта-функцией с некоторым масштабирующим коэффициентом, что позволяет оцепить переходный процесс но виду функции веса.
Функция веса звена связана с его передаточной функцией преобразованием Лапласа, а именно: передаточная функция есть изображение функции веса и связана с ней интегральным преобразованием

В свою очередь переходная функция звена связана с его передаточной функцией преобразованием Карсона, т. е. имеет место интегральное преобразование

 переходный процесс на выходе звена при нулевых начальных условиях может быть определен на основании интеграла Дюамеля-Карсона до переходной функции: переходный процесс на выходе звена при нулевых начальных условиях может быть определен на основании интеграла Дюамеля-Карсона до переходной функции:

где х — вспомогательное время интегрирования, изменяющееся в пределах от нуля до рассматриваемого текущего момента времени I.
Более подробно методика нахождения переходного процесса при произвольном входном воздействии будет рассмотрена в главе 7.
|