Теория систем автоматического управленияНелинейные дискретные системы
Общие сведения
Разделим рассматриваемые ниже нелинейные дискретные системы на два класса.
К первому классу отнесем импульсные и цифровые системы с амплитудно-импульсной модуляцией. Импульсные системы этого класса становятся нелинейными при наличии нелииейностей в их непрерывных частях, а цифровые системы всегда нелинейны из-за наличия квантования по уровню в преобразователях АЦП и ЦАП (см. § 15.1). Нелинейными могут быть и их непрерывные части, а также реализуемые ЦВМ алгоритмы управления.
Исследование цифровых систем при учете всех указанных нелииейностей представляет собой очень сложную задачу. Поэтому будем полагать, что алгоритмы управления являются линейными, а квантованием по уровню можно пренебречь. Последнее, как отмечалось в § 15.1, допустимо при большом числе разрядов в АЦП и ЦАП. Влияние квантования по уровню на протекающие в системах процессы рассмотрено в работе [8].
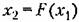 и включено непосредственно за формирующим устройством. и включено непосредственно за формирующим устройством.
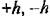
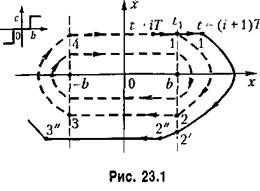
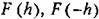 или 0. Таким образом, влияние нелинейности или 0. Таким образом, влияние нелинейности
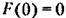 сводится лишь к изменению амплитуды импульсов, что может быть учтено заранее. сводится лишь к изменению амплитуды импульсов, что может быть учтено заранее.
Процессы в нелинейных дискретных системах даже при отсутствии внешних воздействий могут существенно отличаться от процессов в нелинейных непрерывных системах. В первую очередь это обусловлено наличием квантования но времени. Влияние квантования по времени иллюстрирует рис. 23.1, где пунктиром показаны фазовые траектории непрерывной системы, нелинейное звено которой имеет релейную характеристику с зоной нечувствительности. В этой системе существуют периодические колебания, амплитуда которых зависит от начальных условий. Реле срабатывает и отпускает при попадании изображающей точки на линии переключения
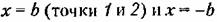 (точки 3 и А). При данной нелинейности такие процессы будут существовать, например, в системе, рассмотренной в § 17.1 (пример 2). (точки 3 и А). При данной нелинейности такие процессы будут существовать, например, в системе, рассмотренной в § 17.1 (пример 2).
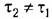 (точка 2"). Таким образом, система стала (точка 2"). Таким образом, система стала
неустойчивой.
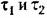 изменяются в процессе работы системы. изменяются в процессе работы системы.
В системах с широтпо-ммпульспой модуляцией процессы будут гораздо более сложными, так как в них изменяется длительность импульсов.
В нелинейных дискретных системах при определенных условиях могут возникать периодические режимы. В случае их устойчивости они условно могут рассматриваться как автоколебания. Однако из-за наличия квантования по времени периодические режимы существенно отличаются от автоколебаний, определение которых было дано в § 16.1.
Во-первых, частота периодических режимов жестко связана с периодом дискретности Т. Для симметричных режимов

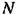 — относительный полупериол колебаний. Это означает, что все возможные частоты периодических режимов известны заранее. — относительный полупериол колебаний. Это означает, что все возможные частоты периодических режимов известны заранее.
 Во-вторых, при установлении периодического режима в системах, непрерывные части которых содержат интегрирующие звенья, может появляться постоянная или медленно изменяющаяся составляющая ошибки даже при отсутствии внешних воздействий и при симметричной нелинейной характеристике. Во-вторых, при установлении периодического режима в системах, непрерывные части которых содержат интегрирующие звенья, может появляться постоянная или медленно изменяющаяся составляющая ошибки даже при отсутствии внешних воздействий и при симметричной нелинейной характеристике.
В-третьих, в одной и той же системе могут возникать периодические режимы с различными частотами колебаний. При этом с течением времени частота может изменяться.
Исследование нелинейных дискретных систем представляет собой сложную задачу Ниже будут рассмотрены лишь некоторые подходы к ее решению.
|