Теория систем автоматического управленияСистемы с широтно-импульсной модуляцией
В процессе широтно-импульсной модуляции (см. § 14.1) изменяется скважность (ширина) импульсов, а их амплитуда (высота) остается постоянной. В зависимости от того, как осуществляется изменение скважности, различают (см. рис 14.3) широпю-импульсную модуляцию 1-го рода (ШИМ-1) и 2-го рода (ШИМ-2).
 и система превращается в импульсную, в которой широтно-импульсный модулятор представляет собой самостоятельное конструктивно законченное устройство. и система превращается в импульсную, в которой широтно-импульсный модулятор представляет собой самостоятельное конструктивно законченное устройство.

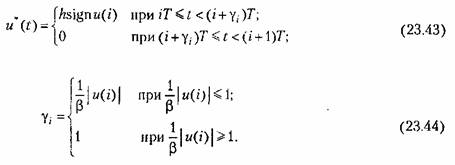
При ШИМ-2 (см. рис. 14.3, б) скважность импульсов определяется в результате сравнения непрерывного входного сигнала с опорным сигналом. Поэтому широтно-импульсный модулятор не вписывается в структуру ЦАП и представляет собой самостоятельное устройство. Сама система в этом случае строится как импульсная (рис. 23.11, а).
В качестве опорного обычно используется пилообразный сигнал (см. рис. 14.3, б)
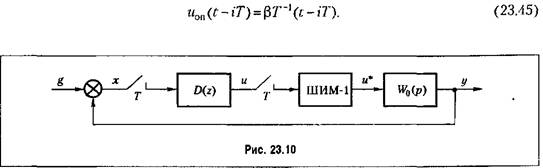

В этом случае скважность импульсов определяется как наименьший положительный корень уравнения

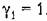 . Например, если на интервалах . Например, если на интервалах
 , то из (23.46) получим выражение , то из (23.46) получим выражение

аналогичное (23.44).
Из рассмотренного примера следует, что введение в систему с ЦВМ широтно-импульсного модулятора 2-го рода (рис. 23.11, б) не имеет смысла. Действительно, чтобы получить на его входе непрерывный сигнал и, ЦАП должен формировать модулированные по амплитуде импульсы, а формирующее устройство должно представлять собой экстраполятор нулевого порядка. Но тогда
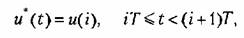
и выражение для скважности импульсов, как и (23.47), совпадает с (23.44). А это означает, что с точки зрения протекающих н системе процессов схемы рис. 23.10 и рис. 23.11, ^эквиваленты, но первая из них конструктивно проще.
Широтно-импульсный модулятор представляет собой нелинейное звено (см. § 14.1). Поэтому определить передаточную функцию приведенной непрерывной части, как это делалось в системах с амплитудно-импульсной модуляцией (рис. 23.2, б), нельзя. Однако можно найти разностное уравнение линейной непрерывной части вместе с щиротно-импульсным модулятором минуя определение передаточной функции. Эту задачу можно решить двумя способами.
Первый способ основан па использовании уравнений состояния.
 соответствуют уравнения состояния (14.71) соответствуют уравнения состояния (14.71)

 имеет вид (14.73) имеет вид (14.73)

где и изменяется по закону (23.43).
Из (23.49) с учетом (23.43) последовательно шаг за шагом получим
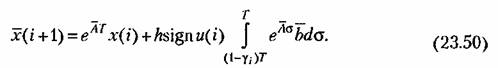
Таким образом, разностными уравнениями линейной непрерывной части системы вместе с широтно-импульсным модулятором будут

 , соответствующих типовым линейным не- , соответствующих типовым линейным не-
прерывным частям, приведены в [57].
Второй способ позволяет определить не векторно-матричпые уравнения (23.51), а разностное уравнение п-го порядка, в ряде случаев более удобное для практического использования.
 : :
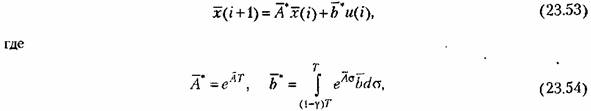
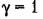 с уравнением (14.75). с уравнением (14.75).
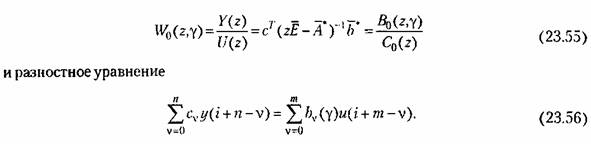 (23.53), как показано в главе 14, соответствует передаточная функция (23.53), как показано в главе 14, соответствует передаточная функция
 можно перейти к разностному уравнению линейной непрерывной части вместе, с ши-ротно-имнульсным модулятором: можно перейти к разностному уравнению линейной непрерывной части вместе, с ши-ротно-имнульсным модулятором:
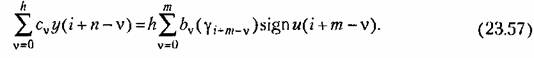
В свою очередь, передаточную функцию (23.55) можно определить но формуле (14.58):
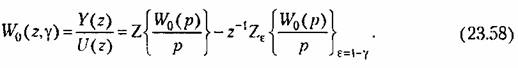
Таким образом, для получения уравнения (23.57) нет необходимости использовать уравнения состояния.
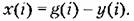
 появляются пульсации. Они особенно опасны в установившемся состоянии, так как пульсирующая составляющая ошибки может оказаться соизмеримой с ее постоянной составляющей. появляются пульсации. Они особенно опасны в установившемся состоянии, так как пульсирующая составляющая ошибки может оказаться соизмеримой с ее постоянной составляющей.
Для выявления пульсаций вместо уравнений (23.51) следует использовать разностные уравнения со смещенным аргументом.


Выражения для матриц (23.60), соответствующих типовым линейным непрерывным частям системы, приведены в [57].
 должна определяться из уравнения (23.46), которое в общем случае является нелинейным. должна определяться из уравнения (23.46), которое в общем случае является нелинейным.
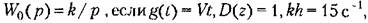
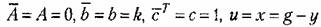 и и
уравнения (23.59) принимают вид
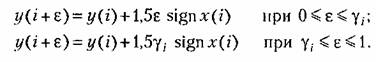
Скважность импульсов согласно (23.44)

Ошибка системы
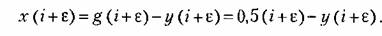
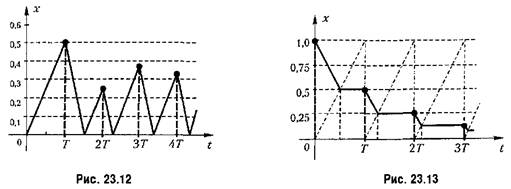
Решив полученные уравнения последовательно шаг за шагом, начиная с последнего, получим переходный процесс, изображенный на рис. 23.12.
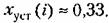 Однако в промежутках между моментами замыкания устанавливаются незатухающие колебания или пульсации. Однако в промежутках между моментами замыкания устанавливаются незатухающие колебания или пульсации.
Составляем уравнения системы:
—ошибка системы
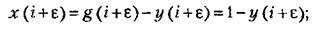
—уравнения (23.59)

—уравнение (23.46)

 Пульсации имеются только в переходном процессе. Пульсации имеются только в переходном процессе.
Следует отметить, что в реальных системах ШИМ пульсации существуют практически всегда, так как даже в астатических системах при отсутствии ошибки от задающего воздействия имеется статическая ошибка от возмущений.
Установившуюся ошибку в типовых режимах удобно представлять в виде суммы

 — пульсирующая составляющая. — пульсирующая составляющая.
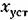 приведены в работе [57]. Так, для рассмотренной в примере 1 системы с ШИМ-1 приведены в работе [57]. Так, для рассмотренной в примере 1 системы с ШИМ-1

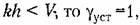 скорость изменения управляемой величины скорость изменения управляемой величины
 ошибка будет непрерывно увеличиваться, т. е. система станет неустойчивой. ошибка будет непрерывно увеличиваться, т. е. система станет неустойчивой.
Пульсирующую составляющую х(г) можно определить точно так же, как это делалось в главе 14, или из уравнений (23.59). В частности, для той же системы с учетом выражения

и формул (23.62) получим:
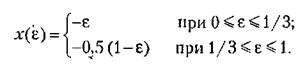
|