Теория систем автоматического управленияТочность в типовых режимах
Для оценки точности системы управления используется величина ошибки в различных типовых режимах. Ниже будут рассмотрены наиболее употребительные режимы.
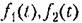 и т. д. Тогда в правой части (5.6) и т. д. Тогда в правой части (5.6)
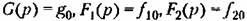 и т. д. Далее необходимо воспользоваться теоремой о конечном значении (см, табл. 7.2) и получить установившееся значение ошибки (статическую ошибку): и т. д. Далее необходимо воспользоваться теоремой о конечном значении (см, табл. 7.2) и получить установившееся значение ошибки (статическую ошибку):
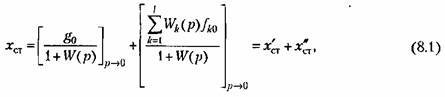

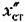 — от возмущающих воздействий. — от возмущающих воздействий.
 — астатической. Величина г определяет порядок астатизма системы. — астатической. Величина г определяет порядок астатизма системы.
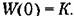 Тогда статическая ошибка от задающего воздействия Тогда статическая ошибка от задающего воздействия

 При этом При этом
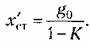
 практически всегда может быть сведена к нулю посредством использования неединичной обратной связи или путем масштабирования. практически всегда может быть сведена к нулю посредством использования неединичной обратной связи или путем масштабирования.
 Поэтому первая составляющая (8.1) обращается в нуль. Поэтому первая составляющая (8.1) обращается в нуль.
Второе слагаемое (8.1) никогда не обращается в пуль, так как даже использование управления с астатизмом высокого порядка и использование принципа управления по возмущению (см. § 9.2) могут обратить в нуль лишь часть слагаемых, находящихся под знаком суммы (8.1),
 . В действительности чувствительному элементу как- . В действительности чувствительному элементу как-
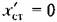 ) )

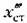 является ошибкой чувствительного элемента. является ошибкой чувствительного элемента.
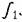 Тогда в статической системе получим Тогда в статической системе получим



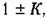 по сути дела, показывает эффективность управления с точки по сути дела, показывает эффективность управления с точки
зрения уменьшения установившейся ошибки.
 Вследствие этого для каждого действующего на систему возмущения необходимо определить факт Вследствие этого для каждого действующего на систему возмущения необходимо определить факт
наличия или отсутствия установившейся ошибки посредством нахождения значения (8.4).
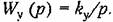 Пусть объект не имеет Пусть объект не имеет


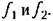 В разомкнутой системе (как показано на рис. 8.1) В разомкнутой системе (как показано на рис. 8.1)
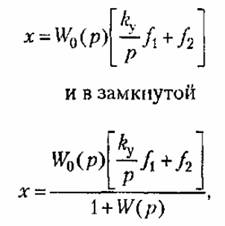
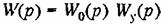 — передаточная функция разомкнутой системы. Отсюда по — передаточная функция разомкнутой системы. Отсюда по
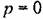


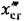 , которую можно рассматривать как возмущение. , которую можно рассматривать как возмущение.
 и т. д. Этот режим имеет смысл только в и т. д. Этот режим имеет смысл только в
следящих системах и системах программного управления.
Используя изображения Карсоиа-Хевисайда, в этом случае получаем
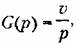
Из общего выражения для ошибки посредством теоремы о конечном значении может быть найдена установившаяся ошибка в этом режиме:

Второе слагаемое этого выражения дает статическую ошибку (при условии, что возмущающие воздействия такие же, как в неподвижном состоянии системы), в которой может быть также учтена ошибка чувствительного элемента.
Первое слагаемое (8.5) имеет смысл только при астатизме первого порядка, т. е. в том случае, когда передаточная функция разомкнутой системы может быть представлена в виде
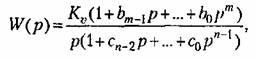
 — коэффициент передачи разомкнутой системы, называемый добротностью по скорости. — коэффициент передачи разомкнутой системы, называемый добротностью по скорости.
Тогда выражение (8.5) приводится к виду

Таким образом, в этом типовом режиме установившаяся ошибка будет слагаться из статической ошибки и добавочной скоростной ошибки, равной отношению скорости задания к добротности системы но скорости:

Так как система может двигаться с различными скоростями, то качество ее удобнее характеризовать не самой скоростной ошибкой, которая является переменной величиной, а значением добротности по скорости

В статических системах первое слагаемое (8.6) стремится к бесконечности; при астатизме выше первого порядка это слагаемое стремится к нулю. Поэтому режим движения с постоянной скоростью используется для оценки точности только систем с астатизмом первого порядка, главным образом следящих систем, для которых такой режим является характерным.
3. Движение с постоянным ускорением. РЗ качестве третьего типового режима используется режим установившегося движения системы с постоянным ускорением
 . Возмущающие воздействия принимаются постоянными, как и во втором типовом режиме. Этот режим имеет смысл только в следящих системах и системах программного управления. . Возмущающие воздействия принимаются постоянными, как и во втором типовом режиме. Этот режим имеет смысл только в следящих системах и системах программного управления.
Аналогично изложенному выше, установившееся значение ошибки в этом режиме может быть найдено из выражения
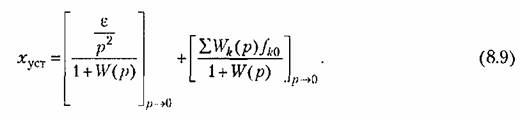
Второе слагаемое (8.9), как и ранее, дает статическую ошибку. Первое слагаемое (8.9) имеет смысл только при астатизме второго порядка, когда передаточная функция разомкнутой системы может быть представлена в виде
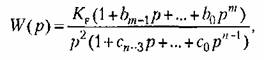
 — коэффициент передачи разомкнутой системы, называемый добротностью по ускорению. — коэффициент передачи разомкнутой системы, называемый добротностью по ускорению.
Тогда выражение (8,9) приводится к виду
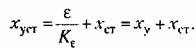
Первое слагаемое (8.10) представляет собой добавочную ошибку от постоянного ускорения. Как и в предыдущем случае, качество системы может быть оценено величиной добротности по ускорению

Этот типовой режим используется только для систем с астатизмом второго порядка, главным образом следящих систем.

В зависимости от конкретного вида системы возмущающие воздействия в рассматриваемом режиме могут оставаться постоянными или меняться,

Более вероятным является случай, когда возмущающие воздействия при движении системы в этом режиме меняются во времени. Это объясняется тем, что при движении по гармоническому закону непрерывно будет меняться направление движения системы, а следовательно, одновременно будет меняться направление действующих в системе сил сухого трения. Этот случай является довольно сложным, и он может рассматриваться только в приложении к конкретным системам. Рассмотрим ошибку определяемую только первым слагаемым выражения (5.19):



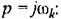

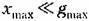 , то, следовательно, модуль знаменателя (8.15) значительно больше единицы. Это позволяет с большой точностью выражение (8.15) заменить приближенным , то, следовательно, модуль знаменателя (8.15) значительно больше единицы. Это позволяет с большой точностью выражение (8.15) заменить приближенным


Последняя формула позволяет легко вычислять амплитуду ошибки в установившемся режиме. Для этого необходимо располагать либо аналитическим выражением для передаточной функции разомкнутой системы, либо иметь экспериментально снятую амплитудно-фазовую частотную характеристику разомкнутой системы.
 в децибелах, т. е. в децибелах, т. е.
 (рис. 8.2, а). (рис. 8.2, а).
Простота выражения (8.16) позволяет легко
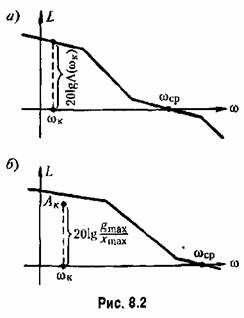
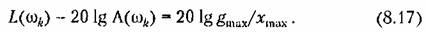
 то ошибка будет больше допустимого значения. то ошибка будет больше допустимого значения.
|