Теория систем автоматического управленияЛинейные алгоритмы управления
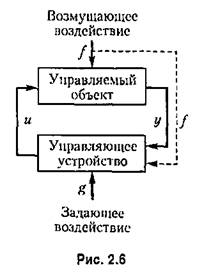
Система автоматического управления, как уже известно, состоит из взаимосвязанных и взаимодействующих между собой управляемого объекта и управляющего устройства (рис. 2.6). Поэтому и качество протекающих в ней процессов зависит как от свойств самого объекта, так и от того, как управляющее устройство управляет этим объектом.
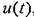 , называется алгоритмом управления. Эта зависимость может быть представлена в виде , называется алгоритмом управления. Эта зависимость может быть представлена в виде
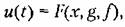
где F— некоторая, в общем случае, нелинейная функция от ошибки х, задающего воздействиями возмущающего воздействия/, а также от их производных и интегралов по времени. Обычно она может быть записана следующим образом:
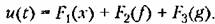
Первое слагаемое соответствует управлению по отклонению, второе и третье — управлению по внешним воздействиям (задающему и возмущающему), которое применяется в комбинированных системах.
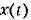 в соответствии с линейной формой в соответствии с линейной формой

1. Пропорциональное управление. В случае пропорционального управления алгоритм управления имеет вид
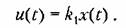
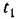 , когда ошибка становится равной нулю, управляющее воздействие будет продолжать действовать в прежнем направлении, вынуждая ее вновь увеличиваться, изменив знак. В результате процесс в системе может стать слишком колебательным и даже расходящимся. , когда ошибка становится равной нулю, управляющее воздействие будет продолжать действовать в прежнем направлении, вынуждая ее вновь увеличиваться, изменив знак. В результате процесс в системе может стать слишком колебательным и даже расходящимся.
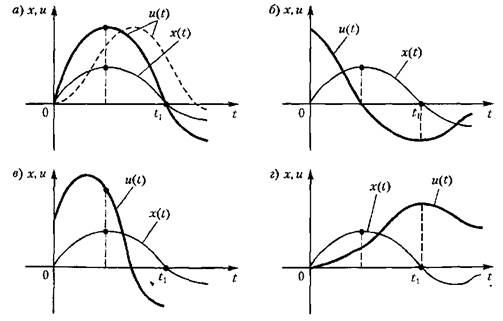
2. Управление по производным. При управлении по первой производной от ошибки осуществляется зависимость
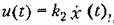
т. е. управляющее устройство реагирует не на саму ошибку, а на скорость ее изменения (рис. 2.7, б), и поэтому действует с упреждением, стремясь не допустить появления ошибки.
Управление по производной не имеет самостоятельного значения, так как в установившемся состоянии, когда ошибка постоянна, производная от ошибки равна нулю и управление прекращается. Однако оно может играть весьма большую роль в переходных процессах и вообще в динамике в качестве вспомогательного средства, так как такое управление позволяет учитывать не только наличие ошибки, но и тенденцию к росту или уменьшению ошибки. Поэтому управление по производной обычно сочетается с управлением по отклонению:

При использовании такого алгоритма управляющее воздействие возникает даже
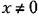
Кроме того, оно изменяет свой знак раньше, чем сама ошибка, т. е. действует с упреждением. В результате введения управления по производной от ошибки увеличивает скорость реакции системы управления, повышает ее быстродействие, что приводит к снижению ошибок в динамике.
В некоторых случаях в алгоритм управления могут вводиться производные более высоких порядков — вторая, третья и т. д. Это еще больше улучшает динамические качества системы автоматического управления. Однако в настоящее время техническая реализация производных выше второго порядка встречает значительные трудности.
3. Интегральное управление. При интегральном управлении осуществляется пропорциональная зависимость между скоростью изменения управляющего-воздействия и ошибкой:
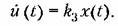
При этом управляющее воздействие получается пропорциональным интегралу от ошибки по времени:
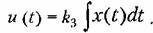
 . Поэтому при возникновении ошибки управляющее воздействие накапливается постепенно, запаздывая по отношению к изменению ошибки. . Поэтому при возникновении ошибки управляющее воздействие накапливается постепенно, запаздывая по отношению к изменению ошибки.
Управление с целью повышения точности системы может осуществляться и по
второму интегралу от ошибки по времени:
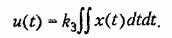
Однако при этом снижение быстродействия станет еще более заметным. 4. Изодромное управление. При изодромном управлении осуществляется зависимость
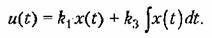
Такое управление сочетает в себе высокую точность интегрального управления с большим быстродействием пропорционального управления. В первые моменты времени при появлении ошибки система изодромного управления работает как система пропорционального управления. Это определяется первым слагаемым в правой части алгоритма управления. В дальнейшем система начинает работать как система интегрального управления, так как с течением времени преобладающее значение начинает приобретать второе слагаемое.
В общем случае алгоритм управления может иметь сложный вид и содержать кроме члена, пропорционального ошибке, также интегралы (для улучшения точности) и производные (для улучшения динамических свойств) от ошибки. Так, например, часто используется изодромное управление с введением первой производной
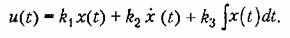
Для линейных алгоритмов управления детально разработаны многочисленные прикладные методы исследования (анализа и синтеза), различные расчетные и экспериментальные приемы определения устойчивости, точности и качества процесса управления, а также схемы конкретных технических устройств формирования линейных алгоритмов.
|