Кузнечно-штамповочное оборудованиеРасчет сил и крутящего момента в кривошипно-ползунном механизме
Силы. В качестве типового примера рассмотрим силы, действующие в вертикальном двухстоечном однокривошипном прессе с расположением маховика на приемном валу.
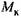 на зуб колеса (рис. 3.1). на зуб колеса (рис. 3.1).
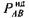 направлена по оси шатуна (рис. 3.2, а) и определяется выражением направлена по оси шатуна (рис. 3.2, а) и определяется выражением

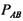 должна быть направлена по общей касательной к кругам трения шарниров на обоих концах шатуна. должна быть направлена по общей касательной к кругам трения шарниров на обоих концах шатуна.
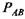 был противоположен направлению его вращения относительно оси шарнира В, от которого передается реакция по шатуну (рис. 3.2, б). При этом надо иметь в виду, что направление касательной не зависит от конструктивного оформления шарнира, т. е. от того, как будет выполнен шарнир: В в виде цапфы или подшипника. был противоположен направлению его вращения относительно оси шарнира В, от которого передается реакция по шатуну (рис. 3.2, б). При этом надо иметь в виду, что направление касательной не зависит от конструктивного оформления шарнира, т. е. от того, как будет выполнен шарнир: В в виде цапфы или подшипника.
Радиус круга трения вращательной пары
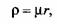
 - коэффициент трения в шарнире; г - радиус цапфы (подшипника). - коэффициент трения в шарнире; г - радиус цапфы (подшипника).
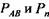 , построим векторный план сил: , построим векторный план сил:
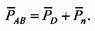
Из векторного треугольника (см. рис. 3.2, б) следует
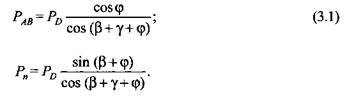
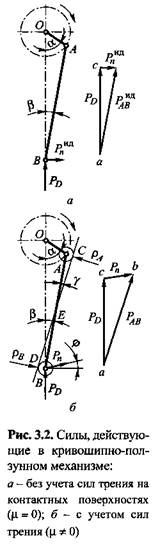
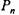 на направляющие ползуна на направляющие ползуна
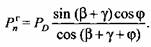
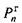 необходимо для расчета шпилек крепления направляющих планок станины. необходимо для расчета шпилек крепления направляющих планок станины.
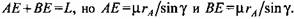
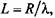 окончательно получаем окончательно получаем
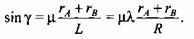
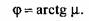
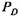 составляет 10... 12 % (для реальных механизмов эта ошибка не превышает 2...3%). Поэтому в дальнейшем при расчете можно считать составляет 10... 12 % (для реальных механизмов эта ошибка не превышает 2...3%). Поэтому в дальнейшем при расчете можно считать
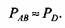
Вертикальная составляющая
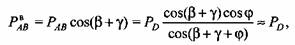
горизонтальная -
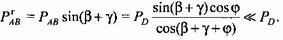
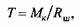
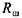 - радиус начальной окружности зубчатого колеса. На зуб колеса действует сила - радиус начальной окружности зубчатого колеса. На зуб колеса действует сила
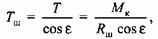
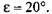
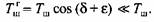
Реакции в опорах. В общем случае реакции в опорах равны геометрической сумме их горизонтальных и вертикальных составляющих:
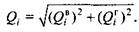
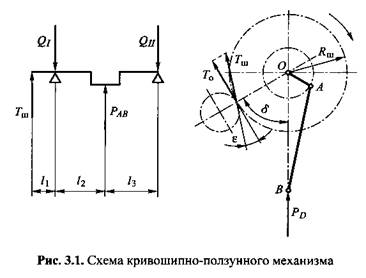
Для рассматриваемой (см. рис. 3.1) силовой схемы кривошипного вала составляющие реакции в опоре I находим по формулам
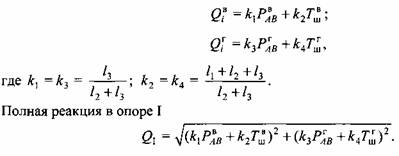
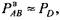
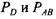
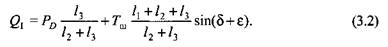
Точно так же находим реакцию в опоре II:
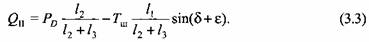
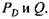
Крутящий момент. Крутящий момент привода для идеальных условий определяется мощностью, затрачиваемой на преодоление силы пластического деформирования заготовки. Для идеального механизма мощность, развиваемая приведенной силой и моментом в точке приведения,

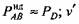 - проекция окружной скорости шарнира А на направление АВ, - проекция окружной скорости шарнира А на направление АВ,
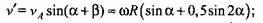
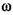 - угловая скорость точки приведения, т. е. шарнира А. - угловая скорость точки приведения, т. е. шарнира А.
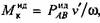
или, подставляя приближенные соотношения для входящих в это выражение величин, получаем
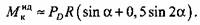
Суммарная мощность привода реального кривошипно-ползунного механизма затрачивается на осуществление работы деформирования и преодоление сил трения в кинематических парах:

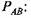
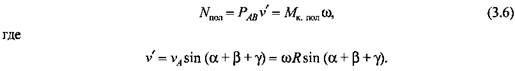
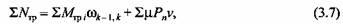
 - момент трения в произвольном шарнире, - момент трения в произвольном шарнире,
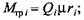
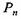 - реакция в плоских поступательно движущихся парах; v - скорость поступательного движения звеньев (ползунов). - реакция в плоских поступательно движущихся парах; v - скорость поступательного движения звеньев (ползунов).
Для кривошипно-ползунного механизма формула (3.7) принимает следующий вид:
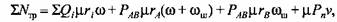
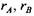 - радиусы шарниров трения; - радиусы шарниров трения;
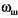 - угловая скорость шатуна. Тогда суммарная мощность - угловая скорость шатуна. Тогда суммарная мощность
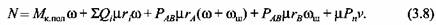
Согласно уравнению (3.6),
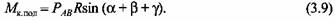
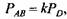 на основании фор- на основании фор-
мул (3.5), (3.8) и (3.9) получаем соотношение для крутящего момента:
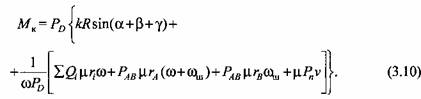
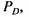 действующей на ползун механизма, действующей на ползун механизма,
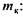
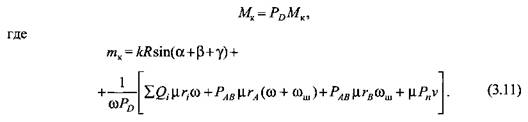
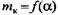 для данного механизма будет неизменной, являясь его особой характеристикой. для данного механизма будет неизменной, являясь его особой характеристикой.
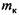 применительно к двухстоечному однокривошипному прессу с расположением маховика на приемном валу. При этом примем ряд допущений: применительно к двухстоечному однокривошипному прессу с расположением маховика на приемном валу. При этом примем ряд допущений:
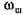 в период рабочего хода невелика, поэтому в период рабочего хода невелика, поэтому
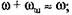
б) третье и четвертое слагаемые в квадратной скобке уравнения (3.27) малы, поэтому ими можно пренебречь;
 и, следовательно, к = 1; и, следовательно, к = 1;
г) для вычисления реакции в опорах двухстоечного пресса можно использо вать формулы (3.2) и (3.3);
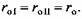 При преобразовании При преобразовании
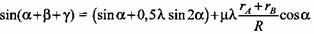
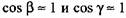 ввиду малости ввиду малости
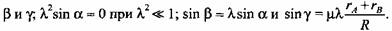 Тогда Тогда
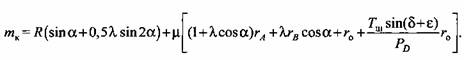
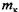 как сумму двух величин: как сумму двух величин:
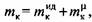
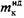 - приведенное плечо идеального механизма, - приведенное плечо идеального механизма,
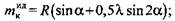
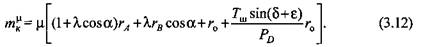
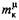 - приращение приведенного плеча, обусловленное трением в кинематических парах реального механизма, - приращение приведенного плеча, обусловленное трением в кинематических парах реального механизма,
Из анализа сил известно, что
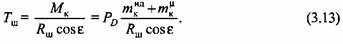
Подставляя выражение (3.13) в (3.12), после преобразований имеем
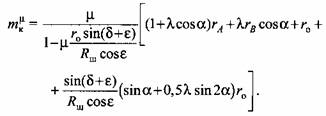
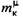 не зависит от угла поворота не зависит от угла поворота
кривошипа, т. е. а = 0. Это приводит к незначительному завышению результатов в пределах требуемой точности расчетов (2...3 %). Следовательно,
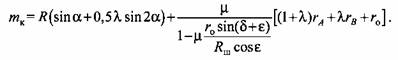
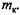 В итоге получаем В итоге получаем
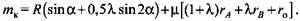
В таком виде в технической литературе и типовых расчетах используют формулу для определения приведенного плеча для любых типов двухстоечных кривошипных прессов с аксиальным кривошипно-ползунным механизмом.
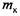 рекомендуют определять по упрощенной формуле: рекомендуют определять по упрощенной формуле:
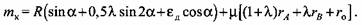
Заметим, что впервые решение для крутящего момента в кривошипно-ползунном механизме с учетом сил трения было дано М.В. Сторожевым.
|