Кузнечно-штамповочное оборудованиеОсновные понятия и уравнения гидродинамики
Силы, приложенные к любому выделенному объему жидкости, ограниченному замкнутой поверхностью, подразделяют на две группы - массовые (объемные) и поверхностные.
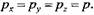 При установившемся течении жидкости или газа изменения массы в рассматриваемом объеме не происходит, что означает равенство объемов втекающей и вытекающей жидкости. При установившемся течении жидкости или газа изменения массы в рассматриваемом объеме не происходит, что означает равенство объемов втекающей и вытекающей жидкости.
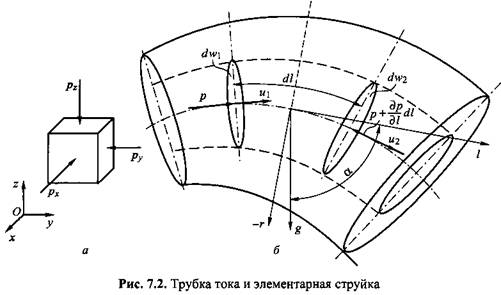
Изучение потока жидкости в трубопроводе показало, что ее частицы, расположенные вблизи оси, движутся с большими скоростями, чем частицы, находящиеся у стенок. При рассмотрении гидродинамических явлений выделяют элементарную струйку, размеры поперечного сечения которой бесконечно малы, а значит, скорость ее течения можно принять постоянной. Для определения понятия элементарной струйки дополнительно вводят понятия линии и трубки тока.
Под линией тока в потоке понимают линию, касательные к которой в каждой точке совпадают с направлением вектора скорости. Для установившегося движения линия тока всегда совпадает с траекторией частиц движущейся жидкости, расположенных на ней. При неустановившемся движении частицы жидкости на линии тока находятся одно мгновение.
Трубкой тока называют трубчатую поверхность замкнутого бесконечно малого контура, образующими которого являются линии тока. Жидкость, заполняющая трубку тока, образует элементарную струйку (рис. 7.2, б).
 перпендикулярное ее образующим, называют живым. В установившемся потоке форма элементарных струек постоянна, а в неустановившемся - непрерывно изменяется. При изучении элементарной струйки уравнения Эйлера записывают в так называемой естественной форме. Координатными осями в этом случае будут касательная, главная нормаль и бинормаль к линии тока, причем проекции действующих сил на бинормаль равны нулю. Обозначая направление касательной к линии тока через / (см. рис. 7.2, б), а главной нормали через г и составляя суммы проекций действующих сил, получаем перпендикулярное ее образующим, называют живым. В установившемся потоке форма элементарных струек постоянна, а в неустановившемся - непрерывно изменяется. При изучении элементарной струйки уравнения Эйлера записывают в так называемой естественной форме. Координатными осями в этом случае будут касательная, главная нормаль и бинормаль к линии тока, причем проекции действующих сил на бинормаль равны нулю. Обозначая направление касательной к линии тока через / (см. рис. 7.2, б), а главной нормали через г и составляя суммы проекций действующих сил, получаем
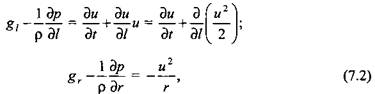
где г - радиус кривизны линии тока.
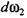 из условия неразрывности струйки будет иметь вид из условия неразрывности струйки будет иметь вид
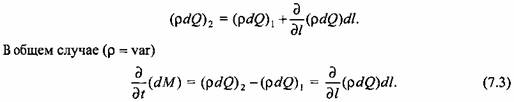
Изменение массы может произойти только в результате изменения плотности р и объема элементарной струйки. Секундное приращение массы можно определить по формуле

из (7.6), после преобразований получим
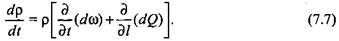
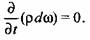 Тогда, согласно уравнению (7.5), Тогда, согласно уравнению (7.5),
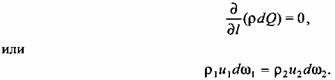
Следовательно, при установившемся движении массовый расход по длине элементарной струйки остается постоянным. При постоянной плотности (р = сош!) скорости в различных сечениях элементарной струйки обратно пропорциональны площадям живых сечений.
В случае неустановившегося движения жидкости при постоянной плотности
 . Тогда уравнение неразрывности (7.7) примет вид . Тогда уравнение неразрывности (7.7) примет вид
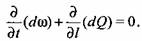
Гидродинамические уравнения Эйлера в естественной форме (7.2) для капельной жидкости можно проинтегрировать и задачу гидродинамики решить с учетом уравнения неразрывности. Согласно рис. 7.2, можно записать

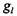 второе уравнение (7.2) можно представить в виде второе уравнение (7.2) можно представить в виде
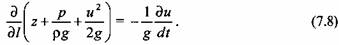
Уравнение (7.8) есть уравнение Бернулли в дифференциальной форме, которое можно интегрировать по длине элементарной струйки:
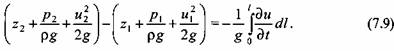
Для неустановившегося движения уравнение Бернулли справедливо только для двух частиц идеальной жидкости, находящихся на одной линии тока в рассматриваемый момент времени. При установившемся движении оно справедливо также и для одной и той же частицы жидкости, находящейся в двух положениях на траектории, ибо последняя совпадает с линией тока.
Выражение правой части уравнения (7.9) характеризует инерционный напор, влияющий на изменение энергии элементарной струйки по ее длине, поэтому его можно рассматривать как дополнительный источник энергии при
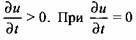 имеет имеет
место установившееся движение.
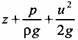 характеризует гидродинамический напор. При установившемся движении идеальной жидкости напор постоянен и равен полной энергии элементарной струйки. Полную энергию (гидродинамический напор) при установившемся движении идеальной жидкости можно рассматривать как характеризует гидродинамический напор. При установившемся движении идеальной жидкости напор постоянен и равен полной энергии элементарной струйки. Полную энергию (гидродинамический напор) при установившемся движении идеальной жидкости можно рассматривать как
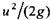 Следовательно, при уменьшении потенциальной энергии на такую же величину возрастает кинетическая энергия, и наоборот. Следовательно, при уменьшении потенциальной энергии на такую же величину возрастает кинетическая энергия, и наоборот.
Рассматривая элементарную струйку реальной жидкости, необходимо учитывать гидродинамические потери, обусловленные возрастающими при течении силами трения между отдельными слоями жидкости. Уравнение Бернулли для реальной жидкости можно записать в виде
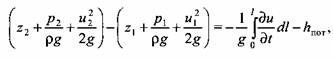
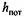 - гидродинамические потери между двумя сечениями элементарной струйки жидкости. - гидродинамические потери между двумя сечениями элементарной струйки жидкости.
|