Кузнечно-штамповочное оборудованиеУравнение Бернулли для течения жидкости в трубопроводе
Поток жидкости в трубопроводе может быть ламинарным или турбулентным. При ламинарном течении частицы жидкости перемещаются параллельно оси трубопровода не перемешиваясь. При турбулентном течении частицы пульсируют в поперечном направлении и их траектории являются сложными кривыми. Исследование скоростей в поперечных сечениях потока жидкости в трубопроводе показывает их неравномерное распределение: при ламинарном течении они изменяются по параболическому закону, при турбулентном (местные осредненные) - по показательному или логарифмическому.
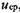 , равной отношению интегрального расхода жидкости через поперечное сечение трубопровода к его площади: , равной отношению интегрального расхода жидкости через поперечное сечение трубопровода к его площади:
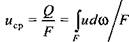
где Р - площадь поперечного сечения трубопровода.
Из уравнения неразрывности (7.5) для элементарной струйки, распространенного на весь поток в трубопроводе, следует, что средние скорости обратно пропорциональны площади его поперечного сечения.
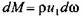 и проинтегрировать по всей площади: и проинтегрировать по всей площади:
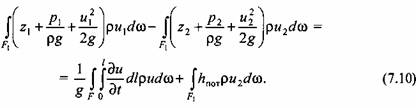
Интегралы в левой части уравнения (7.10) выражают напоры потоков в первом и во втором сечениях, а интегралы в правой части уравнения - инерционный напор и потери на преодоление гидравлических сопротивлений соответственно.
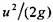 которыми обладает масса жидкости, равная секундному расходу через поперечное сечение: которыми обладает масса жидкости, равная секундному расходу через поперечное сечение:


Коэффициент Кориолиса а зависит от характера распределения скорости течения по сечению трубопровода. Так, если при ламинарном течении
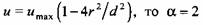 (см. рис. 7.1). Для турбулентного течения при (см. рис. 7.1). Для турбулентного течения при
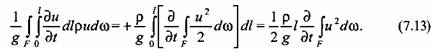

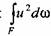 можно также выразить через среднюю скорость: можно также выразить через среднюю скорость:
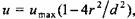
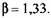 Коэффициенты а и (3 определяют по опытным данным и характеризуют степень неравномерности распределения скоростей течения по сечению трубопровода. Коэффициенты а и (3 определяют по опытным данным и характеризуют степень неравномерности распределения скоростей течения по сечению трубопровода.
С учетом уравнений (7.11)—(7.14) выражение (7.10) можно привести к виду
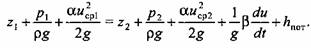
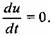
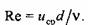
При Rе < 2320 течение ламинарное, а при Rе > 2320 - турбулентное.
В трубопроводах гидравлических прессов в большинстве случаев течение жидкости турбулентное, однако при использовании минеральных масел может быть и ламинарным.
|