Динамика адсорбции.

При выборе адсорбента особое внимание должно быть сосредоточено на трех аспектах транспортных явлений в адсорбционных слоях. Это диффузия внутри самих частиц, массоперенос фазы внедрения и перепад давлений в тол-стых слоях.

Диффузия внутри частиц:

В ходе адсорбционных процессов скорость диффузии внутри частиц в каждый момент времени зависит от размеров отдельных частиц (которые в случае частиц сферической или цилиндрической формы могут быть охарактеризованы величиной их радиуса l), времени, прошедшего с момента начала диффузии, и эффектного коэффициента диффузии для данной системы, Deff. Последний параметр эквивалентен DABEP/r, где DAB - коэффициент диффузии растворенного вещества в данной жидкости, ЕР - доля пустот внутри частиц, а r - их кривизна.

Deff/l является хорошим показателем того, насколько легко внутреннее вещество частиц может участвовать в адсорбционных процессах. Таким обра-зом, эффективной (быстрой) адсорбции благоприятствует высокий коэффици-ент диффузии или малый диаметр частиц либо оба эти фактора вместе. Однако, как будет показано ниже, соображения, связанные с оценкой перепада давлений, обычно перевешивают все аргументы, связанные с выбором в пользу мелких частиц.

Массоперенос фазы внедрения: Существует математическая корреляция (при условии предложения, что в системе применяются неподвижные слои адсорбента):

к данной системе число Рейнольдса (pvsdp/m, где четыре параметра обозначают соответственно, плотность жидкости, диаметр частиц и вязкость жидкост и ), jD - j-ф актор Колб урна -Хил тона. Последний равняется (k/vs)Sc0,667, где k - коэффициент массопереноса для системы жид-кость-частица, а Sc - число Шмидта, равное m/pDAB.

В этом выражении массоперенос фазы внедрения лучше всего характеризуется параметром k: чем выше его значения, тем эффективнее массоперенос. Величина k определяется главным образом свойствами жидкости (плотностью, вязкостью и коэффициентом диффузии) и поверхностной скоростью, а также одним из параметров адсорбента - диаметром частиц dp.

Можно заметить, что величина k меняется обратно величине dp в степени 0,415. Поэтому для определенной жидкости при данной скорости потока десятикратное уменьшение диаметра частиц привело бы примерно к трех-кратному повышению коэффициента массопереноса.

Такая корреляция также показывает, что даже к большему - почти четырехкратному - росту коэффициента массопереноса привело бы десятикратное увеличение скорости. Однако увеличивать значение k методом повышения скорости неразумно, поскольку время контакта адсорбционного слоя с жидкостью обратно пропорционально величине скорости, то есть, чем быстрее жидкость проходит через слой адсорбента, тем меньше времени последний может участвовать в процессе.

Перепад давлений в толстых слоях адсорбента:

Большинство адсорбционных установок работает при сравнительно невысоких перепадах давления. Для сохранения такого положения обычно стремятся использовать адсорбент с возможно более крупными частицами. Другим фактором, обеспечивающим низкий перепад давления, является эксплуатация установки при низких скоростях жидкости, что способствует установлению равновесия между жидкостью и адсорбентом. Чтобы обеспечить низкую скорость, адсорбент, как правило, укладывают в короткие толстые слои большого диаметра, а не в длинные и тонкие.

При таких технологических условиях трубопроводы, клапаны и штуцеры, вероятно, будут подвергаться воздействиям таких же перепадов давления, что и адсорбционный слой. В любом случае лучше все проверить дважды. Хорошим средством для такой проверки служит уравнение Эргуна, приемлемое при условии низких скоростей потока, проходящего через короткие адсорбционные слои:

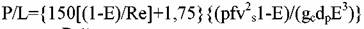число Рейнольдса соответствует определению, описанному выше, L - расстояние, на которое перемещается поток, проходя через слой адсорбента, а Е - доля пустот в адсорбционном слое, то есть порозность слоя (но не доля пустот внутри частиц).

Расчеты адсорбционных систем многогранны и зависят от поставленных задач. Достаточно много примеров по этому направлению имеется литературных источниках. Остановимся только на наиболее простых расчетах, которые, однако, не приводятся в литературе, так как требуют знания специальных зависимостей.