Вязкость и пластичность нефтепродуктовЭмпирические уравнения зависимости вязкости от температуры
Интерполяционные формулы и уравнения с двумя постоянными. Предложено значительное число эмпирических формул, связывающих вязкость жидкостей с их температурой (см. обзоры М. М. Кусакова и К. С. Рамайя , там же приводится подробная библиография). Наиболее простые из них представляют собой обычные интерполяционные формулы или их варианты, принятые при подборе эмпирических формул. К их числу относятся формула Пуазейля:
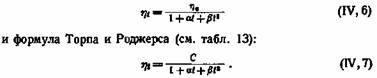
Постоянные величины, входящие в эти формулы (а, 0, С), не имеют физического смысла. Близки к таким формулам уравнения температурной зависимости текучести, предложенные Бинга-мом.

где А—постоянная.
Однако эта формула имеет весьма ограниченное применение. Более широко применяется основная формула Бингама с тремя константами
Для воды, спиртов и других жидкостей, содержащих гидро-ксильную группу, формула (IV, 9) неприменима. Лучшие результаты дает эмпирическое уравнение Бингама с четырьмя постоянными:
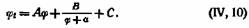
Уравнения этого типа будут передавать вязкостно-температурную зависимость тем точнее, чем больше в них постоянных величин. Однако возрастание числа постоянных усложняет их применение, так как количество экспериментальных измерений, которые нужно производить для вычисления постоянных, не меньше их числа. Для применения формул (IV, б, 7 и 9) необходимо измерять вязкость по крайней мере при трех температурах.
Эмпирические формулы с двумя постоянными обычно передают с достаточным приближением зависимость вязкости от температуры простых нормальных жидкостей.
Для многих нормальных жидкостей, а также для некоторых не слишком вязких аномальных жидкостей, применимы эмпирические соотношения типа формулы Слотта:

которая была проверена на 70 жидкостях (преимущественно нормальных), исследованных Торпом и Роджером.
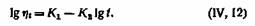
Недавно А. И. Бачинский отметил, что формула


предложенная им для смазочных масел. Согласно этой формуле необходимо приписать одинаковый наклон кривой rj = /(/) для всех минеральных масел, что совершенно не соответствует действительности. Неудачна также использованная в некоторых английских работах формула Дарси :
"-СТ. <IV>15>
так как она отражает линейную зависимость 1/rj от /, что не имеет места в сколько-нибудь широком интервале температур.
Значительный интерес представляет группа эмпирических уравнений, разработанная для выражения вязкостно-температурной зависимости нефтепродуктов, расплавленных стекол и аналогичных по своим механическим свойствам аномальных жидкостей.
Сравнительно давно И. Д. Афанасьев на обширном экспериментальном материале (автолы, вапоры и т. д.) показал, что многие масла в координатах grjt — Igt дают прямые или кривые, близкие к прямым. Степенная или экспоненциальная зависимость вязкости от температуры лежит в основе всех эмпирических формул рассматриваемого типа. Для расплавленных стекол, у которых вязкость очень сильно зависит от температуры, Ле-Шателье предложил формулу

где е—основание натуральных логарифмов; Т—абсолютная температура; а и С константы. В логарифмической форме уравнение (IV, 16) имеет вид

П. П. Лазарев , а также Б. В. Дерягин и И. Я. Хананов нашли, что более хорошие результаты можно получить, если ввести в эту формулу еще одну постоянную щ:

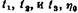 можно вычислить из соотношения можно вычислить из соотношения
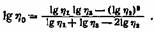
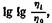 а по оси ординат — а по оси ординат —
температура t. Тогда постоянная А будет равна отрезку на оси ординат, отсекаемому прямой, построенной на основании уравнения (IV, 18), а постоянная В будет равна тангенсу угла наклона этой прямой.
Близко к уравнению Ле-Шателье первое уравнение К. С. Ра-майя , предложенное для нефтепродуктов

Оно отличается от уравнений (IV, 16) коэфициентом А и тем, что а для всех жидкостей становится постоянным и равным двум.
Широкое распространение в смазочном деле получило уравнение Вальтера, которое также является вариантом уравнения Ле-Шателье, В экспоненциальной форме оно имеет вид
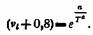
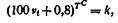
где v выражено в сантистоксах.
Дважды логарифмируя это уравнение, получим
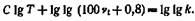
Вводя обозначение g g к = Л и С = В, получаем обычную логарифмическую форму уравнения Вальтера:
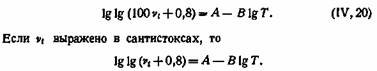
На графике в координатах g g (100 vt + 0,8) или g g (vt + + 0,8) и g T для многих нефтепродуктов получаются прямые линии.
Широкое применение уравнения Вальтера связано с тем, что на его основе построены простые номограммы для вычисления вязкости масел и других нефтепродуктов при различных температурах.
Измерив вязкость при двух достаточно далеко отстоящих одна от другой температурах, нанеся на номограмму g g (?х + 0,8), lg lg (v2 + О8) lg7 и ]g T2 и проведя через полученные точки прямую, можно найти vt при заданной Т.
Однако это уравнение имеет существенные недостатки. Его постоянные, как и постоянные всякой другой чисто эмпирической формулы, лишены физического смысла. Логарифмирование приводит к сглаживанию вязкостно-температурной зависимости, а двойное логарифмирование в еще большей степени выравнивает реальную вязкостно-температурную зависимость. По этой причине наклоны прямых
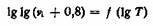
Для жидких нефтепродуктов, сильно разнящихся по своим вязкостно-температурным свойствам, мало отличаются один от другого. С другой стороны, постоянная величина В, характеризующая наклон, в действительности не является постоянной для данного образца масла и зависит от точек, взятых для расчета. Это уравнение является лишь известным приближением, полезным в тех случаях, когда нужно быстро вычислить величину вязкости по двум измерениям, даже допуская при этом значительную ошибку. В последнее время обнаружено, что некоторые масла вообще не подчиняются уравнению Вальтера , особенно при температурах ниже 20—40° . М. П. Воларович рекомендует брать вязкость для вычисления по номограмме уравнения Вальтера не при 50° и 100° или 38,2° и 98е, как это делалось раньше, а при нуле и 100°, что несколько улучшает применимость уравнения.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
Некоторые весьма полезные вязкостно-температурные уравнения представляют собой теоретические уравнения в которые введены дополнительные эмпирические постоянные. В таком виде эти уравнения становятся применимыми и ко многим аномальным жидкостям. В частности, к ним относятся формулы, связанные с уравнением Рамана:
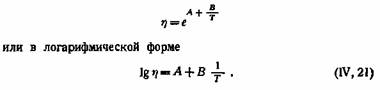
В этом уравнении А равно величине, к которой стремится вязкость ?? при увеличении температуры; обычно она называется вязкостью при бесконечной температуре. Величина В имеет смысл энергии активации течения . Это уравнение вполне приемлемо для маловязких жидкостей, но непригодно для таких, как минеральные масла и вязкие нефтепродукты. Б. В. Дерягин и М. М. Кусаков показали, что, введя в уравнение третью постоянную и несколько преобразовав его по сравнению с (IV, 21), можно придти к уравнениям
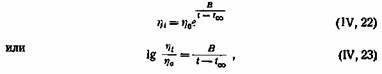
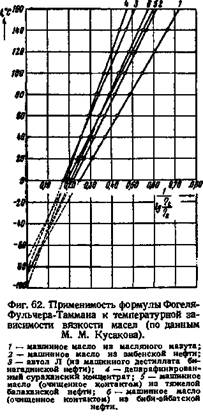
дающим хорошие результаты для смазочных масел. Уравнение (IV, 22) известно под названием формулы Фогеля-Фульчера-Таммана. Фульчер с успехом применял его для расплавленных стекол, а Тамман—для переохлажденных жидкостей.
Согласно М. М. Кусакову постоянные этого уравнения щ, В и /с имеют более или менее отчетливый физический смысл. Постоянная ??0 является вязкостью при бесконечно большой температуре, В показывает, насколько уменьшается вязкость с повышением температуры. Формально она равна числу градусов, на которые нужно нагреть жидкость, чтобы ее вязкость была в 10 раз больше 70, наконец, величина /> является температурой, при которой вязкость обращается в бесконечность, т. е. температурой г при которой жидкость застывает. Следует, однако, отметить, что температура бесконечной вязкости не совпадает с температурой застывания, а величина В недостаточна для характеристики пологости вязкостно-температурной кривой.
Подобно постоянным других уравнений постоянные уравнения Фогеля-Фульчера-Таммана могут быть определены аналитическим или графическим путем.
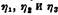 , и подстановка , и подстановка
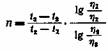
приводят к следующим зависимостям:
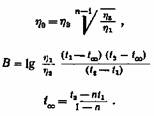
Как видно из этих формул, аналитическое вычисление постоянных щ, В и too связано с довольно сложными расчетами. Для практических целей достаточно пользоваться менее точным, но более простым графическим способом их определения . Формулу (IV, 23) можно переписать в следующем виде:
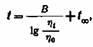
откуда следует, что температура / является линейной функцией
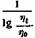
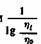 температурные значения у и t дают прямую линию. Тангенс угла наклона этой прямой будет равен В, а отрезок, отсекаемый ею на оси /, будет равен /то. Применимость рассматриваемого уравнения к смазочным маслам подтверждается данными М. М. Кусакова (фиг. 62). Трудная задача номографирования уравнения Фогеля-Фульчера Таммана была недавно успешно решена Г. В. Виноградовым. температурные значения у и t дают прямую линию. Тангенс угла наклона этой прямой будет равен В, а отрезок, отсекаемый ею на оси /, будет равен /то. Применимость рассматриваемого уравнения к смазочным маслам подтверждается данными М. М. Кусакова (фиг. 62). Трудная задача номографирования уравнения Фогеля-Фульчера Таммана была недавно успешно решена Г. В. Виноградовым.

или в логарифмической форме
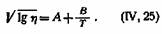
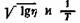 зависимость вязкости от температуры изображается прямой. Вычисление постоянных уравнений (IV, 23) настолько просто, что не нуждается в объяснении. зависимость вязкости от температуры изображается прямой. Вычисление постоянных уравнений (IV, 23) настолько просто, что не нуждается в объяснении.
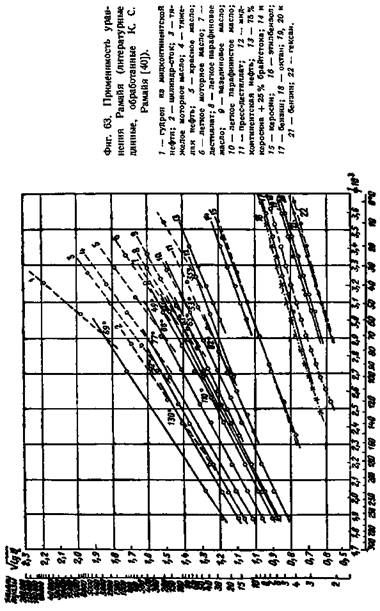
С помощью собственных измерений и путем обработки многочисленных литературных данных К. С. Рамайя подтвердил применимость своей формулы к смазочным маслам и другим нефтепродуктам в широком интервале температур (фиг. 63). Формула дает лучшие результаты для вязких жидкостей и неприменима для бензина и низших углеводородов. Для этих жидкостей подходит неизмененная формула Рамана.
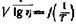 обычно имеют один, редко два перелома. Температура перелома у различных жидкостей неодинакова. Во многих случаях с повышением вязкости жидкости она смещается в сторону высоких температур. Однако Г. И. Фукс и Н. Г. Пучков показали, что если повышать вязкость масел растворением в нем присадок, то точка перелома не меняется . Таким образом, она зависит от состава жидкости, а не только от вязкости. обычно имеют один, редко два перелома. Температура перелома у различных жидкостей неодинакова. Во многих случаях с повышением вязкости жидкости она смещается в сторону высоких температур. Однако Г. И. Фукс и Н. Г. Пучков показали, что если повышать вязкость масел растворением в нем присадок, то точка перелома не меняется . Таким образом, она зависит от состава жидкости, а не только от вязкости.
К. С. Рамайя объясняет изменение наклона
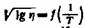 как как
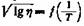
|