Зависимость деформации от времени. Тиксотропия, тиксолабильность, реопексия и дилатенция

У реальных тел не существует мгновенных деформаций. Установление равновесия между внешними и внутренними силами занимает некоторое, иногда большое, время. В литературе пользуются термином мгновенные деформации, но это лишь означает, что они занимают весьма малое время1. Из максвелловского уравнения релаксации (I, 14) вытекает, что время является не менее существенным фактором деформации, чем величина напряжения, Исследование кинетики деформации имеет большое значение. Представляет интерес рассмотреть следующие три элемента временной зависимости деформаций: влияние времени действия нагрузки, изменение тела во времени после снятия нагрузки и влияние скорости нагружения.

1.             Зависимость деформации от времени действия нагрузки.

Основные виды зависимости деформации от времени действия деформирующей силы можно свести к пяти типам, представленным на фиг. 13. У ньютоновской жидкости (кривая 7) деформации е представляют собой линейные функции времени /. Это положение является прямым следствием закона вязкости Ньютона. Характер зависимости деформации от времени тела Бингама-Воларовича не отличается от аналогичной зависимости ньютоновского тела— ниже предела текучести деформация не имеет места, а выше него она пропорциональна времени.

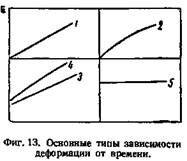
В противоположность ньютоновской жидкости деформация идеально упругого тела (тела Гука) не зависит от времени (кривая 5). Между этими крайними видами зависимости располагаются кривые не ньютоновских жидкостей и невдеально пластичных и упругих тел.

У псевдопластичных жидкостей деформация е является нелинейной функцией времени (кривая 2). В частности, расход жидкости через трубу или капилляр не пропорционален времени. Этим объясняется отмеченная выше плохая воспроизводимость измерений аномальной вязкости.

Упруго-пластичные тела дают кривые 3 или 4. Часть их деформации, связанная с упругим компонентом, не зависит от времени действия деформирующей силы, другая же часть, связанная с вязкостью, является функцией времени. Если вязкость нормальная, то последняя часть деформации пропорциональна времени (кривая 3). При аномальной вязкости зависимость деформации от времени носит более сложный характер (кривая 4).

Последействие нагрузки и разгрузки. После прекраще ния действия деформирующей силы тела со временем могут или вернуться к первоначальной форме, или полностью либо частично сохранить новую форму. В первом случае деформация упруга, во втором пластична или соответственно упруго-пла стична.

Величина нагрузки отражается на последействии. Исследования П. А. Ребиндера с сотрудниками, Г. В. Виноградова и других показывают, что нагрузка определяет не только упругую или остаточную деформацию, но частично также кинетику деформации и возвращения тела к первоначальной форме после снятия нагрузки. Для многих смазок, обладающих упругостью, это время увеличивается по мере приближения к пределу текучести. Таким образом, переход упругих Деформаций в пластичные может не быть резким.

В литературе отсутствует общепринятая терминология эффектов изменения деформации во времени под нагрузкой и после разгрузки. П. А. Ребиндер называет нарастание деформации во времени под действием постоянного напряжения последействием нагрузки, а убывание деформации после снятия нагрузки последействием разгрузки. Г. В. Виноградов первое обозначает термином прямое последействие, второе — обратное последействие. Последействие нагрузки Бингам называет упругим предэффектом и последействие разгрузки — последействием. В дальнейшем мы будем пользоваться терминологией П. А. Ребиндера.

Конкретные примеры последействий представлены на фиг. 14, изображающей результаты измерения тангенциального сдвига

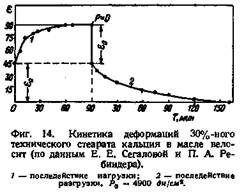
пластинки, погруженной в 30%-ный раствор технического стеа-рата кальция в велосите (измерения Е. Г. Сегаловой и П. А. Ребиндера ). Под действием постоянной нагрузки деформация развивается и только через 60—90 мин. заканчивается. После снятия нагрузки обнаруживается значительное последействие разгрузки. Деформация вполне обратима: через 150—180 мин. после разгрузки она исчезает.

Интересно отметить, что скорость деформации имеет наибольшее значение в момент нагрузки или разгрузки и во времени постепенно снижается до нуля или очень малой величины. Такой вид кинетики последействия характерен для большинства деформаций.

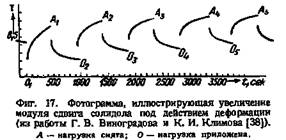
Аналогичные данные получены Г. В. Виноградовым и К. И. Климовым при измерении деформации солидолов (фиг. 17) с помощью разработанного ими метода исследования упругих свойств смазок . Во времени деформация увеличивается, а скорость деформации падает. После снятия нагрузки в моменты Л17 А2 и т. д. отчетливо проявляется упругое последействие разгрузки.

Г. В. Виноградов и К. И. Климов нашли, что кинетика последействия нагрузки солидолов при нагрузках ниже предела текучести подчиняется соотношению

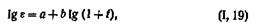
где е — деформация; / — время действия напряжения; а и b константы.

Константа Ь оказалась постоянной в широком интервале напряжений. Аналогичная связь между деформацией и временем найдена другими авторами для асфальтов.

Кинетика последействия разгрузки солидолов по Виноградову подчиняется соотношению

где /i —время после снятия нагрузки; с и d—постоянные.

При классификации реальных тел с целью выбора параметров деформации и их измерения нельзя ограничиваться установлением связи деформации с напряжением, а необходимо также определить последействия нагрузки и разгрузки. Измерением зависимости е от т нельзя отличить упругое тело от неупругого и соответственно упруго-пластичное от более сложного пластичного тела. Уравнение тела Бингама-Воларовича применимо к реальным телам, у которых деформация во времени ниже предельного напряжения сдвига настолько мала, что ею можно пренебречь. Следует отметить, что интервалы времени действия силы не должны быть слишком велики. Известно, что реальные пластичные тела при чрезвычайно большом времени действия напряжения могут необратимо деформироваться, если даже нагрузка ниже предельного напряжения сдвига.

Одним из способов упрощения описания сложных деформаций реальных тел является метод моделирования . Он сводится к тому, что исследуемое тело заменяется моделью, состоящей из элементов, имитирующих отдельные реологические свойства. Упругость имитируется идеальной пружиной; вязкость —поршнем с просверленными отверстиями, погруженным в вязкую жидкость; предельное напряжение сдвига— ползуном (фиг. 15). Сочетая эти элементы последовательно или параллельно, можно получить системы, моделирующие реологические свойства тел. Последовательное сочетание пружины и поршня моделирует максвелловскую жидкость (фиг. 15, г), последовательное сочетание пружины, ползуна, еще одной пружины и поршня —тело Шведова (фиг. 15, д).

Рассмотрим деформацию растяжения модели тела Шведова. Если приложить малую силу, то будет растягиваться только первая пружина. При этом величина деформации пропорциональна силе, а сама деформация вполне обратима Когда приложенная сила возрастет до силы трения ползуна, он начнет двигаться. Это будет соответствовать началу течения тела. Скорость течения зависит от вязкости жидкости, протекающей через отверстия поршня. При

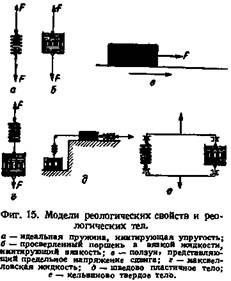
течении часть деформации является упругой, так как она заключается в растягивании пружины между ползуном и поршнем. После разгрузки деформация частично обратима (пружины), но значительная ее часть остаточна (положение ползуна).

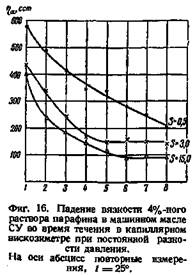
Метод моделирования дает качественное или полуколичественное описание деформации, но для многих практических целей он отвечает своему назначению, особенно в сочетании с точным измерением отдельных параметров, имеющих непосредственное значение для применения материала. 3. Изменение сопротивления деформации под влиянием деформирующей силы. У многих дисперсных систем нагрузка не только производит деформацию, но и изменяет сопротивление деформации. На фиг. 16 показаны результаты измерения кажущейся вязкости 4%-ного раствора парафина в машинном масле СУ. Измерения проводились в U-образном капиллярном вискозиметре нашей модификации с горизонтальным капилляром (см. главу III). Прибор позволяет перепускать жидкость из одного колена в другое при постоянной разности давлений (в данном опыте 25 см вод. ст.) и измерять вязкость во время каждого перепускания. Полученные данные показывают, что кажущаяся вязкость значительно уменьшается во время течения.

Г. В. Виноградов наблюдал увеличение модуля сдвига соли-долов под действием деформации (фиг. 17).

Различные изменения сопротивления деформации (изменения вязкости, модуля упругости, предельного напряжения сдвига)

могут быть разбиты на четыре типа, представленных на фиг. 18, где по оси ординат отложено сопротивление деформации F, а по оси абсцисс — время /.

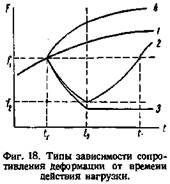
В рассматриваемых системах F обычно самопроизвольно меняется. Этот процесс является следствием старения дисперсных систем и возникающих вследствие этого изменений их свойств. Старение может привести как к росту F, так и к его падению. Кривая 1 изображает первый случай. Он встречается чаще второго,

Если в момент t1 приложить деформирующую силу, то может оказаться, что она не окажет влияния на сопротивление деформации. Дисперсные системы, в которых нагрузка не влияет на сопротивление деформации, называются тиксостабильными.

Возможно и снижение F, которое будет продолжаться в течение времени действия нагрузки tl—/2 или до того, как будет достигнуто минимальное значение F, присущее системе. После снятия нагрузки в момент t2 многие дисперсные системы самопроизвольно (без нагревания или каких-либо иных внешних воздействий) восстанавливают первоначальное сопротивление деформации. Такие системы получили название тиксотропных (кривая 2). Время /2—t3, в течение которого достигается первоначальное значение сопротивления деформации, называют временем тиксо-тропного восстановления сопротивления деформации (в частности, вязкости или предельного напряжения сдвига).

Другие дисперсные системы самопроизвольно не восстанавливают своего сопротивления деформации или восстанавливают его настолько медленно, что этим явлением можно пренебречь. Они названы тиксолабильными системами (кривая 3). Наконец в некоторых телах внешние силы вызывают увеличение сопротивления деформации (кривая 4). Автор вместе с Е. А. Смолиной наблюдал более быстрый рост вязкости масел при низких температурах при медленном течении, чем в спокойном состоянии (табл. 1). Это явление можно назвать реопексией.

Термины гиксостабильность, тиксотропия, тиксолабильность и реопексия заимствованы из коллоидной химии. Все эти свойства впервые наблюдались у коллоидных растворов и суспензий, Аналогичные явления имеют место в металлах и других технических твердых телах. Например, существует много общего между упрочнением металлов при деформации и реопексией или между так называемым гистерезисом механических свойств и тиксо-тропией. Однако представляется более правильным в области реологии нефтепродуктов сохранить коллоидно-химическую терминологию. По своим механическим свойствам нефтепродукты значительно ближе к гелям, золям и суспензиям, чем к твердым телам, а некоторые из них являются типичными дисперсными системами.

Тиксотропия впервые наблюдалась у гидрофобных гелей . При встряхивании или других механических воздействиях такие гели разжижались. После пребывания в покое полученные золи самопроизвольно вновь превращались в гели. Время превращения этих золей в гели называется временем тиксотропного застудневания. В дальнейшем было показано, что кажущаяся вязкость псевдопластичных тел также может быть тиксотропной . П. А. Ребиндер и Д. С. Великовский изучали тиксотро-пию, измеряя предельное напряжение сдвига.

Тиксотропия обнаружена у многих пластичных и псевдопластичных нефтепродуктов. Иногда отождествляют аномалию вязкости с тиксотропией, что в общем виде неправильно. Существенным признаком тиксотропии является обратимость сопротивления деформации. Именно по этому признаку тиксотропия отличается от тиксолабильности. С точки зрения применения нефтепродуктов представляет интерес не только разжижаемость смазок и масел при низких температурах, но и их способность восстанавливать свою консистенцию.

Первые попытки оценить тиксотропию сводились к измерению времени тиксотропного застывания или восстановления вязкости. В дальнейшем было показано, что это время зависит не только от свойств дисперсной системы, но и от разжижающего механического воздействия. К. Ф. Жигач с сотрудниками разработал интересный метод изучения тиксотропии, в котором показатели тиксотропии связаны с величиной механического воздействия.

М. П. Воларович и В. Л. Вальдман , а также Грин и Вельтман характеризуют тиксотропию площадью или шириной петли гистерезиса при снятии прямой и обратной кривых течения в ротационном вискозиметре (фиг. 19). В. Л. Вальдман называет отношение тах мерой тиксотропии. г}тт является

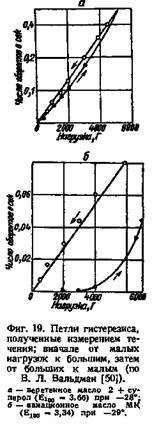
ньютоновской вязкостью и дается углом наклона обратной прямой /V=/(G); ?7max — аномальная вязкость, вычисленная на правом участке петли гистерезиса, при самых малых градиентах скорости. Описанный метод оценки тиксотропии представляет несомненный интерес, так как имеет отчетливый физический смысл и количественный характер. Однако нам кажется, что он должен быть дополнен показателем восстанавливаемости вязкости.

П. А. Ребиндер и его сотрудники характеризуют тиксо-тропию падением и нарастанием во времени предельного напряжения сдвига и других упруго-пластичных параметров систем. Очевидно, что если на оси ординат фиг. 14 отложить не деформацию, а сопротивление деформации, функцией которой она является, то кривая кинетики последействий нагрузки и разгрузки будет кривой тиксотроп-ныхпревращений исследуемого объекта. Эта методика строго количественная и позволяет детально исследовать тиксо-тропию упруго-пластичных тел.

Процесс восстановления сопротивления сдвигу протекает благодаря действию внутренних сил и измерение этих сил имеет большое значение. К. С. Рамайя ввел понятие о тиксотропной силе минеральных масел при низких температурах и предложил вискозиметрический метод для ее оценки. Развитие этого метода требует более четкой диференциации аномалии вязкости и тиксотропии.

Тиксолабильность подобно тиксотропии впервые была обнаружена на некоторых гелях, которые при встряхивании разжижаются, но вторично самопроизвольно не застывают. А. И. Рабинерсон наблюдал необратимое снижение вязкости золей. Это свойство было также обнаружено у некоторых нефтепродуктов (в частности, нами и К. С. Рамайя у минеральных масел при низких температурах и Г. В. Виноградовым у смазок). Но так как тиксолабильность часто объединяется с тиксотропией, то трудно сказать, насколько велико ее практическое значение. Учитывая характер структурообразования парафинов в маслах, можно думать, что это свойство встречается достаточно часто, по крайней мере у минеральных масел при низких температурах и смазок, загущенных твердыми углеводородами.

Фрейндлих и Юлиусбургер назвали реопексией эффект понижения времени тиксотропного застудневания золя при медленном вращении жидкости. Вскоре было показано, что всякое медленное течение способствует застудневанию и повышению сопротивления деформации многих тиксотропных золей, в то время как быстрые деформации оказывают разжижающее действие. По абсолютной величине этот эффект у охлажденных масел невелик (табл. 1) и, вероятно, не играет заметной роли в применении нефтепродуктов, но он интересен для изучения природы сопротивления деформации дисперсных систем и при вискозиметрии.

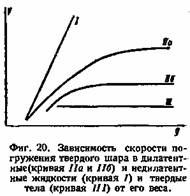
Было замечено , что если в 43—45%-ную суспензию чистого кварца в воде медленно погружать твердый шарик, то скорость его движения пропорциональна приложенной силе, т. е. система ведет себя как жидкость. С увеличением скорости сопротивление резко нарастает и становится независимым от деформирующей силы, что отвечает поведению твердого тела (фиг. 20). Этот эффект получил название дилатенции.

Дилатенция имеет место у нетиксотропных дисперсных систем в узком интервале высоких концентраций. Характерно, что силы взаимодействия частиц очень малы. Достаточно добавить к кварцевому песку немного соли, вызывающей коагуляцию, как дилатенция исчезает. Помимо кварцевого песка она была обнаружена у гелей кремнекислоты, 10%-ного раствора нафтената кальция в нефтяном дестиллате, суспензии канифоли в жидком парафине и некоторых других дисперсных системах.

Фрейндлих объясняет этот эффект следующим образом. При медленном погружении твердого тела в дилатентную систему частицы раздвигаются и не оказывают значительного сопротивления деформации. При быстром погружении они не успевают сдвинуться, создается местное повышение концентрации и вскоре плотность упаковки частиц, лежащих перед движущимся телом, настолько возрастает, что дальнейшее его движение становится невозможным.

Как известно, многие битумы ведут себя как жидкости при медленных деформациях и как твердые, даже хрупкие, тела при быстрых деформациях. Является ли это проявлением ди-латенции или оно связано с другими явлениями — трудно решить без специальных исследований. Различие заключается в том, что концентрация твердых частиц в битумах намного ниже, чем у типичных дилатент-ных систем, а примеси не

оказывают такого большого влияния на эффект. Можно думать, что влияние скорости на деформацию битума связано не с твердыми. частицами, а с ассоциированными молекулами.