РадиоведениеКлассификатор целей

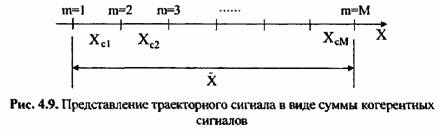
Почти все задачи радиолокации - обнаружение, измерение координат, селекция движущихся целей и другие - можно рассматривать с единых позиций классификации целей. Каждой цели, ее состоянию и местоположению приписывается своя функция отражения. Синтез оптимального классификатора целей основывается на статистической теории многоальтернативного обнаружения, т.е. строится многоканальная система (рис. 4.8), каждый канал которой настроен на оптимальное обнаружение траекторного сигнала, соответствующего одной из всего класса функций отражения целей. Устройство сравнения определяет канал с максимальным выходным сигналом.
 соответствует цель с известным распределением по пространству (х, у, г) локальных характеристик рассеяния - амплитуды и фазы отраженной волны, т.е. портрет цели. Другие отличия целей (скоростные, поляризационные) будут рассматриваться отдельно. соответствует цель с известным распределением по пространству (х, у, г) локальных характеристик рассеяния - амплитуды и фазы отраженной волны, т.е. портрет цели. Другие отличия целей (скоростные, поляризационные) будут рассматриваться отдельно.
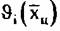 однозначно соответствует траекторный сигнал однозначно соответствует траекторный сигнал


 . Такое . Такое
представление функции когерентности траекторного сигнала в виде ступенчатой функции намного упрощает задачу синтеза классификатора, не снижая общности результатов.
Траекторный сигнал на входе классификатора

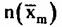 - сумма внутреннего шума и фона. - сумма внутреннего шума и фона.
 апертуры апертуры
реальной антенны, считая, что используется суммарная ДН антенны.
Полагаем также, что благодаря высокому разрешению РСА все объекты наблюдаются раздельно (разрешаются), следовательно, синтез классификатора можно проводить для случая наличия траекторного сигнала только одного объекта и шума. Задача синтеза оптимального классификатора сводится к определению апостериорной вероятности наличия траекторного сигнала цели с заданной функцией отражения.
Синтез классификатора для случая пространственно-когерентной цели Функцию отражения такой цели можно записать в виде суммы L точек:
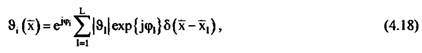
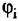 одинакова для всех точек. одинакова для всех точек.
Такая функция отражения в сантиметровом диапазоне волн может существовать только у специальных объектов в определенных условиях, однако с увеличением длины волны РЛС (дециметры-метры) фазу зеркальных точек функции отражения большинства объектов определяют более устойчивые закономерности: расстояние между точками, ракурс цели, геометрические формы цели и т.п. В этом случае для классификации могут быть использованы и фазовые соотношения между отдельными точками цели.
Известно, что для сигнала из М некоррелированных частей с аддитивным белым шумом апостериорная вероятность

 - априорная вероятность наличия цели. - априорная вероятность наличия цели.
 на каждом из М интервалов синтезирования. Тогда на каждом из М интервалов синтезирования. Тогда

 ); );
 не изменяет положения не изменяет положения
 . Апостериорная вероятность 1-го класса в этом случае равна: . Апостериорная вероятность 1-го класса в этом случае равна:

 - отношение сигнал/шум для всего - отношение сигнал/шум для всего
траекторного сигнала.
Таким образом, оптимальный классификатор выполняет операцию корреляции входного траекторного сигнала с опорным траекторным сигналом каждой цели в отдельном канале на каждом интервале синтезирования и затем суммирует модули корреляционных моментов всех интервалов синтезирования. Алгоритм выполнения этих операций в каждом

канале для i -й цели можно представить в виде:
Рассмотрим сигнальную часть (без шумов) корреляционного интеграла в 1-м канале на т-м интервале синтезирования:

и представим ее в частотной области:

 - спектр траекторного сигнала 1-й цели. - спектр траекторного сигнала 1-й цели.
В свою очередь спектр принимаемого траекторного сигнала
 - спектр функций отражения всех объектов, сигналы которых присутствуют в траекторном сигнале; - спектр функций отражения всех объектов, сигналы которых присутствуют в траекторном сигнале;
 - частотная характеристика системы преобразования функция отражения - траекторный сигнал. - частотная характеристика системы преобразования функция отражения - траекторный сигнал.

 - спектр функции отражения 1-й цели. - спектр функции отражения 1-й цели.
Корреляционный интеграл с учетом этих преобразований и перехода из частотной области в пространство целей будет иметь вид:

Где


 определяется частотной характеристикой РСА определяется частотной характеристикой РСА
 (рис. 4.10). (рис. 4.10).
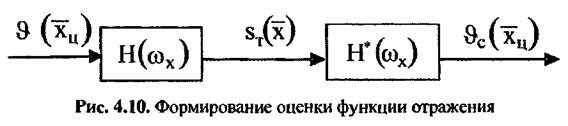
 соответствует сглаженной функции соответствует сглаженной функции
 переходной характеристики РСА, которая в свою очередь определяется угловым размером траекторного сигнала (синтезированной апертуры). Напомним, что импульсная переходная характеристика РСА, т.е. отклик РСА на точечную цель, есть функция неопределенности РСА: переходной характеристики РСА, которая в свою очередь определяется угловым размером траекторного сигнала (синтезированной апертуры). Напомним, что импульсная переходная характеристика РСА, т.е. отклик РСА на точечную цель, есть функция неопределенности РСА:
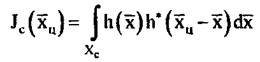
 корреляционный момент между сглаженным изображением объектов и функцией отражения i-й цели. корреляционный момент между сглаженным изображением объектов и функцией отражения i-й цели.
 данного канала (без учета шумовой составляющей): данного канала (без учета шумовой составляющей):
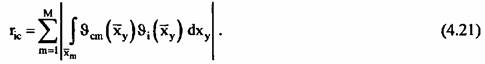
 , которые не изменяют алгоритма классификации (рис. 4.11). , которые не изменяют алгоритма классификации (рис. 4.11).

 , а корреляционный интеграл , а корреляционный интеграл


 для одноточечной цели. для одноточечной цели.
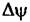 : :

то сглаженное комплексное изображение цели будет иметь вид:


Синтез классификатора для случая пространственно-некогерентной цели. Амплитуды и фазы каждой точки функции отражения такой многоточечной цели случайны и независимы между собой, а ее модель соответствует большинству объектов радиовидения.
Полагаем, что каждая точка в изображении разрешается и функция отражения цели


Апостериорная вероятность (4.19), усредненная по случайным амплитудам и фазам, при условии разрешения каждой точки


 - отношение - отношение
сигнал/шум для (-й точки в т-м интервале синтезирования.
 (без (без
шумов) подобно предыдущему случаю можно представить в виде:

 - модуль функции отражения i -й точки 1-й цели. - модуль функции отражения i -й точки 1-й цели.
Корреляционный момент 1-й цели (сигнальная часть)


Таким образом, оптимальный классификатор целей со случайной функцией отражения формирует на каждом интервале синтезирования комплексное изображение каждой разрешаемой точки наблюдаемых объектов и суммирует модули изображений каждой точки отдельно на всех интервалах синтезирования. Накопленное некогерентно изображение объектов коррелируется с модулем эталонной функции отражения 1-й цели.
Структура классификатора представлена на рис. 4.13.




Производя замену переменных X! = Ах + х2 и учитывая, что корреляционная функция траекторного сигнала зависит только от разности Ах, можно представить корреляционную функцию изображения в виде
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение

 намного больше изменения намного больше изменения
 и двойной интеграл превращается в произведение интегралов. и двойной интеграл превращается в произведение интегралов.
Первый интеграл от корреляционной функции траекторного сигнала с учетом (4.14)

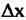 в бесконечных пределах в бесконечных пределах


Корреляционная функция изображения в этом случае

 имеет вид имеет вид

Дисперсия изображения пропорциональна распределению мощности отраженного сигнала по полоске дальности, а интервал корреляции
(на уровне 0,7) при заданной весовой функции W (х)



|