РадиоведениеФазоразностный алгоритм автофокусировки
Этот алгоритм дает результаты, сравнимые с результатами алгоритма на основе оценки средней доплеровской частоты (СДЧ). Он позволяет точно оценивать квадратичную (или более высокого порядка) фазовую ошибку при существенно меньших объемах вычислений.
В этом разделе рассмотрена реализация фазоразностного алгоритма только для оценки квадратичной фазовой ошибки. Однако, как и в случае с алгоритмом оценки СДЧ, возможно его расширение для оценки ошибки более высокого порядка.
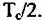 Сигналы в каждом канале дальности первой и второй подапертур описываются выражениями (6.48) и (6.49). Затем сигналы первой и второй подапертур перемножаются: Сигналы в каждом канале дальности первой и второй подапертур описываются выражениями (6.48) и (6.49). Затем сигналы первой и второй подапертур перемножаются:
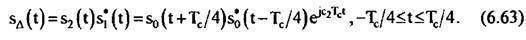
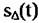 формирует корреляционную формирует корреляционную
функцию комплексных изображений каждой из подапертур:
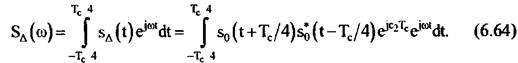
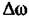 , можно вычислить значение квадратичной фазовой ошибки: , можно вычислить значение квадратичной фазовой ошибки:

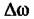 определяет знак квадратичной фазовой ошибки. Для повышения точности оценки можно также усреднить корреляционную функцию по всем каналам дальности. определяет знак квадратичной фазовой ошибки. Для повышения точности оценки можно также усреднить корреляционную функцию по всем каналам дальности.
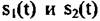 удаляет квадратичную фазовую ошибку на краях подапертур. удаляет квадратичную фазовую ошибку на краях подапертур.
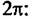
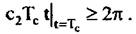
Таким образом, минимальное значение коэффициента квадратичной фазовой ошибки, которое вызывает смещение пика корреляционной функции, а следовательно, и определяет минимальный дискрет вычисления коэффициента, составляет
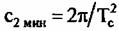
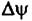 на краях интервала синтезирования при использовании алгоритма оценки СДЧ и фазоразностного алгоритма: на краях интервала синтезирования при использовании алгоритма оценки СДЧ и фазоразностного алгоритма:
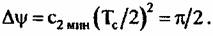
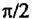 приводит к снижению мощности сигнала точечной цели на I дБ, что в большинстве задач является допустимым. приводит к снижению мощности сигнала точечной цели на I дБ, что в большинстве задач является допустимым.
Автофокусировка по сигналам точечных отражателей. При
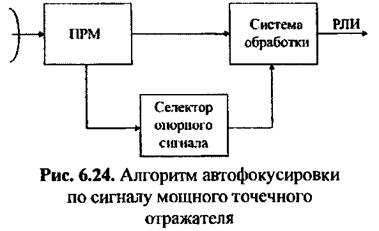
высоком разрешении в зоне обзора почти всегда находятся несколько ориентиров (точечных отражателей). Алгоритм автофокусировки по сигналам от точечных отражателей обеспечивает высокую точность компенсации фазовых нестабильностей, поэтому данный метод получил наибольшее распространение. Структурная схема РСА с фокусировкой изображения по сигналу точечного объекта представлена на рис. 6.24. Если сигнал ориентира намного превышает суммарный сигнал от других объектов и местности в пределах одного элемента разрешения по дальности и ширины ДН реальной антенны, то он может быть выделен из общего сигнала путем стробирования по дальности. В этом случае селектор опорного сигнала представляет собой селектор сигнала от полоски дальности, в которой находится опорный ориентир.
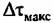
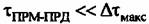 . Однако . Однако
быстрые флуктуации имеют малую дисперсию и могут не учитываться. Таким образом, в течение периода повторения РСА фазовые флуктуации сигналов объектов в зоне обзора обладают сильной корреляционной связью.
Вышеизложенное позволяет сделать вывод о том, что сигнал отдельного точечного объекта можно использовать для компенсации фазовых искажений сигналов всех объектов, расположенных в определенной зоне одновременного обзора РСА. При этом устраняется влияние не только ТН, но и тропосферных нестабильностей и нестабильностей приемопередающего тракта. При непосредственном использовании сигнала выбранного объекта в качестве опорного сигнала системы обработки положение любого объекта на изображении будет пропорционально азимуту этого объекта, отсчитываемому от координаты опорного объекта.
Однако в большинстве случаев ЭПР опорного объекта сравнима с ЭПР фона местности в пределах того же элемента разрешения по дальности и ширины ДН реальной антенны, и качество фокусировки будет низким вследствие помех от фона местности. Поэтому требуется принимать специальные меры при формировании опорного сигнала.
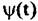 , принимаемую на фоне внутренних , принимаемую на фоне внутренних
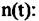
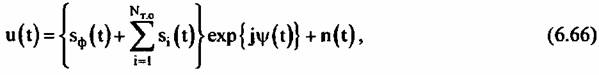
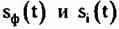 - сигналы от фона и - сигналы от фона и
1-го точечного объекта:
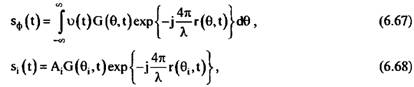
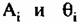 - соответственно - соответственно
комплексная амплитуда сигнала 1-го объекта и его азимутальное положение относительно центра зоны обзора.
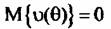 и корреляционной функцией: и корреляционной функцией:
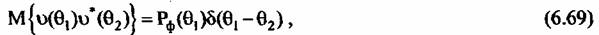
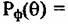
Изменение дальности до отражателя в зоне обзора можно аппроксимировать квадратичной зависимостью:

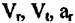 - соответственно радиальная и тангенциальная скорости и радиальное ускорение движения ФЦА по отношению к центру зоны обзора. - соответственно радиальная и тангенциальная скорости и радиальное ускорение движения ФЦА по отношению к центру зоны обзора.
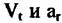 вычисляются по данным навигационной системы вычисляются по данным навигационной системы
и используются при расчете опорной функции:
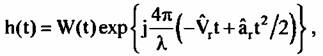
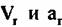
После перемножения с опорной функцией сигналы фона и точечных объектов примут вид:
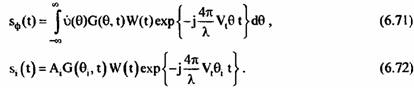
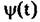 определяются фазовым набегом, определяются фазовым набегом,
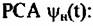
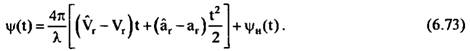
Фазовые нестабильности |/и(1) в общем случае являются некоторой неизвестной случайной функцией.
Сигнал точечных объектов (отражателей) содержит информацию о фазовых искажениях траекторного сигнала и может использоваться для автофокусировки изображения. В качестве точечных отражателей могут выступать малоразмерные объекты, уголковые отражатели и т.п. Селектор опорного сигнала измеряет фазу этого сигнала
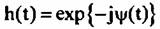 . Непосредственное измерение фазовых . Непосредственное измерение фазовых
нестабильностей предпочтительней оценки коэффициентов линейного и квадратичного фазовых набегов, так как позволяет устранить фазовые набеги более высоких порядков.
Реальные точечные объекты обычно имеют значительно меньшую ЭПР. Поэтому для автофокусировки в канале дальности с опорным объектом необходима дополнительная селекция сигнала объекта на фоне помехи от подстилающей поверхности.
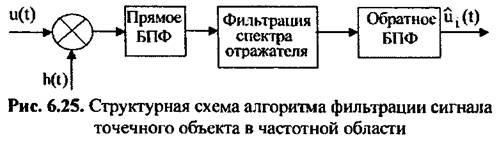
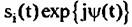 выделяется из помех выделяется из помех
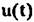
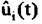 выполняется обратное БПФ (ОБПФ). Его фаза выполняется обратное БПФ (ОБПФ). Его фаза
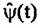 используется для формирования фокусирующей опорной функции, устраняющей траекторные нестабильности: используется для формирования фокусирующей опорной функции, устраняющей траекторные нестабильности:
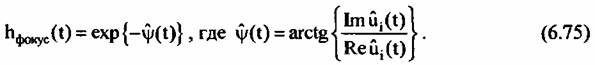
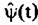 содержит все нестабильности траекторного сигнала. Такой способ вычисления опорной функции уменьшает влияние флуктуации опорного сигнала на РЛИ, однако полученное изображение оказывается сдвинутым на величину доплеровской частоты сигнала опорного объекта. Для обеспечения независимости изображения от положения опорного объекта спектр сигнала на выходе фильтра перед ОБПФ обычно сдвигают к нулевой доплеровской частоте. содержит все нестабильности траекторного сигнала. Такой способ вычисления опорной функции уменьшает влияние флуктуации опорного сигнала на РЛИ, однако полученное изображение оказывается сдвинутым на величину доплеровской частоты сигнала опорного объекта. Для обеспечения независимости изображения от положения опорного объекта спектр сигнала на выходе фильтра перед ОБПФ обычно сдвигают к нулевой доплеровской частоте.
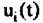
можно аппроксимировать следующей зависимостью:
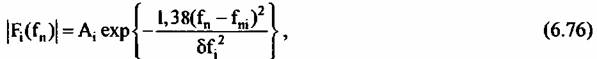
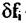 - ширина спектра сигнала 1-го объекта. - ширина спектра сигнала 1-го объекта.
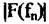 на выходе БПФ (рис. 6.26). Тогда в случае стационарного фона в на выходе БПФ (рис. 6.26). Тогда в случае стационарного фона в
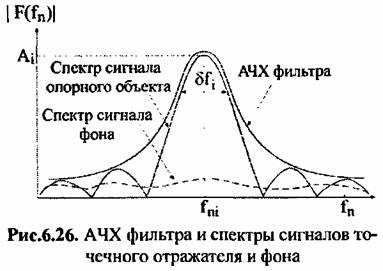
окрестности объекта оптимальная АЧХ фильтра для выделения изображения опорного объекта определяется известным выражением:

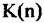 - аппроксимация модуля спектра сигнала объекта (6.76): - аппроксимация модуля спектра сигнала объекта (6.76):

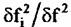 - отношение ширины спектра сигнала к ширине элемента разрешения по частоте, которая выражает степень расфокусировки изображения точечного объекта. - отношение ширины спектра сигнала к ширине элемента разрешения по частоте, которая выражает степень расфокусировки изображения точечного объекта.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
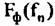 в окрестности изображения объекта: в окрестности изображения объекта:
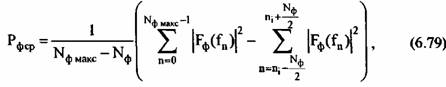
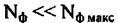 - число фильтров в пределах ширины спектра сигнала - число фильтров в пределах ширины спектра сигнала
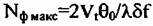 - максимальное число фильтров в пределах ширины спектра сигнала от фона местности. - максимальное число фильтров в пределах ширины спектра сигнала от фона местности.
Степень расфокусировки изображения точечного объекта определяется отношением

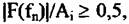 и результаты расчетов по всем фильтрам усредняются. и результаты расчетов по всем фильтрам усредняются.
Если в зоне обзора в разных элементах дальности присутствует несколько точечных объектов, то требования к ЭПР также уменьшаются. Структурная схема системы обработки сигналов РСА с автофокусировкой изображения по нескольким точечным объектам приведена на рис. 6.27.
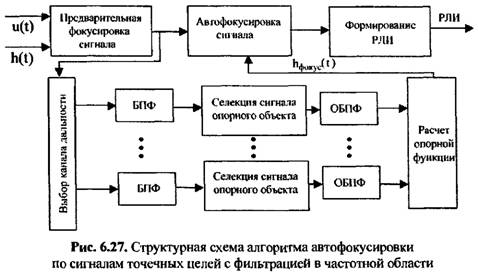
Выбор канала дальности основан на том, что мощность сигнала в канале дальности с опорным объектом превышает среднюю мощность траекторного сигнала, усредненную по всем каналам дальности. Для этого в каждом канале дальности вычисляется коэффициент

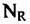 - число каналов дальности. - число каналов дальности.
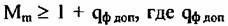 определяется в соответствии с выражением (6.74). определяется в соответствии с выражением (6.74).
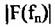 и нахождения средней мощности и нахождения средней мощности
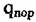 = =
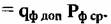
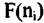 на амплитудно-частотную характеристику фильтра на амплитудно-частотную характеристику фильтра
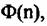 рассчитанную по выражению (6.77). Далее выполняется ОБПФ. рассчитанную по выражению (6.77). Далее выполняется ОБПФ.
Расчет опорной функции осуществляется путем усреднения фазы, измеренной для всех объектов. Однако это требует измерения полной фазы каждого опорного объекта (с учетом перескоков через значение 2л) и устранения начальной фазы сигнала каждого объекта.
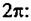
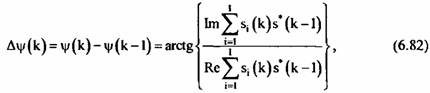
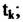
I - число объектов, по которым осуществляется автофокусировка.
В этом случае опорная функция для фокусировки определяется путем
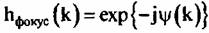 , ,
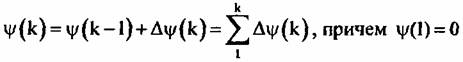
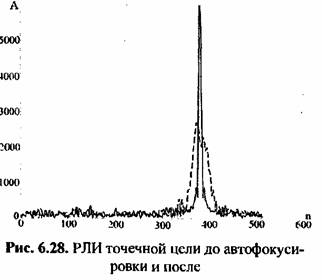
На рис. 6.28 представлен пример использования алгоритма автофокусировки на массиве траекторного сигнала с уголковым отражателем. Потенциальное разрешение по азимуту составляет 1 м. После предварительной фокусировки по данным от навигационной системы разрешение составило 4 м (штриховая линия). После автофокусировки (сплошная линия) было достигнуто разрешение 1,1 м, что близко к оптимальному.
Нескомпенсированная
фазовая ошибка, рассчитанная
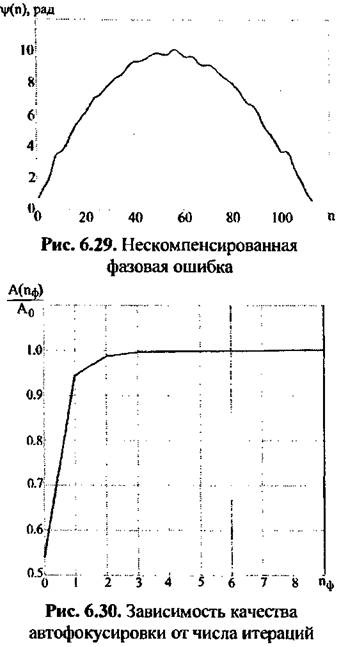
в соответствии с данным алгоритмом, представлена на рис. 6.29, Видно, что фазовая ошибка имеет ярко выраженный квадратичный характер, однако присутствуют и ошибки другого порядка. На рис. 6.30 показано увеличение амплитуды сигнала изображения отражателя после нескольких последовательных фокусировок (итераций). Из рисунка видно, что основной эффект фокусировки РЛИ достигается на первом шаге.
Алгоритм автофокусировки по сигналам точечных отражателей обладает блестящими возможностями для компенсации фазовых ошибок высокого порядка в широком классе наблюдаемых целей. Однако данный алгоритм предъявляет достаточно жесткие требования к точечности целей. Это приводит к необходимости применения дополнительных алгоритмов отбора объектов, подходящих для процедуры автофокусировки, что в свою очередь приводит к увеличению вычислительной сложности алгоритма. Несмотря на это алгоритм остается не очень требовательным к вычислительным ресурсам и может быть достаточно просто реализован на современной вычислительной базе.
Автофокусировка изображения методом формирования динамического фазового портрета. Недостатком алгоритма фокусировки по сигналам точечных отражателей является необходимость выбора не только мощных, но и точечных отражателей. С этой целью используются различные дополнительные процедуры, основанные на вычислении корреляции амплитуды и фазы сигнала вдоль траектории. Кроме того, неточечность цели приводит к необходимости итерационных процедур оценки фазы.
Однако существует метод автофокусировки, не требующий оценки точечности цели, - метод формирования динамического фазового портрета, при котором измеряется квадратичная фазовая ошибка.
Динамический фазовый портрет - это радиолокационное изображение объекта, получаемое с высоким пространственным разрешением, сигнал каждой точки которого пропорционален разности фаз сигналов в двух разнесенных во времени (а также в пространстве и времени) каналах РСА соответствующего разрешаемого участка.
Сигнал, отраженный от неподвижной точечной цели, может быть представлен в виде:
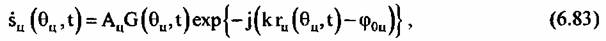
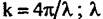 - длина волны РСА; - длина волны РСА;
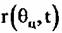 — расстояние от цели до фазового центра антенны. — расстояние от цели до фазового центра антенны.
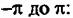
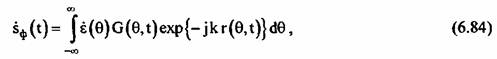
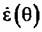 - комплексная амплитуда сигнала; 0 - азимутальная координата отражателя. - комплексная амплитуда сигнала; 0 - азимутальная координата отражателя.
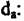

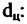

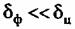
При однородной местности в районе цели математические модели квадратурных составляющих сигнала фона можно представить в виде гауссовского белого шума:

После компенсации квадратичного фазового набега, обусловленного изменением расстояния РЛС-цель, траекторный сигнал, отраженный от точечной цели, имеет вид:

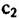 - нескомпенсированная квадратичная фазовая ошибка, - нескомпенсированная квадратичная фазовая ошибка,
Так как мощность сигнала фона при обнаружении цели обычно значительно (на 15-20 дБ) превышает мощность внутренних шумов, то влиянием внутреннего шума пренебрегаем. Задача оценки квадратичной фазовой ошибки сводится к задаче оценки параметра ЛЧМ сигнала на фоне белого гаусовского шума:
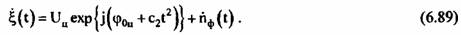
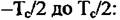
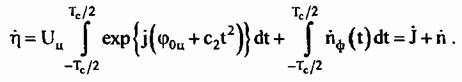
Сигнальная часть имеет вид:
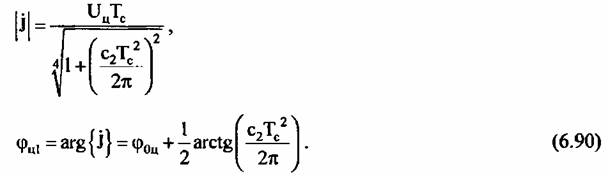
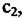 но и от начальной фазы. Следовательно, необходимо использовать дополнительный канал. но и от начальной фазы. Следовательно, необходимо использовать дополнительный канал.
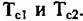 Амплитуда и фаза сигналов цели и фона описываются выражениями: Амплитуда и фаза сигналов цели и фона описываются выражениями:
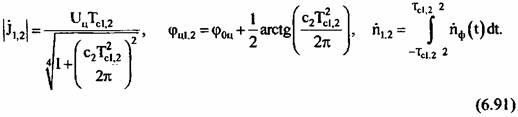
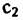 по сигналам, формируемым первой и второй апертурами. Сигнал на входе такой двухканальной системы обработки описывается выражением: по сигналам, формируемым первой и второй апертурами. Сигнал на входе такой двухканальной системы обработки описывается выражением:

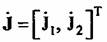 ; ;
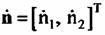
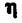 описывается четырехмерным распределением его квадратурных составляющих. Для гауссовского случайного процесса эта плотность вероятности описывается выражением: описывается четырехмерным распределением его квадратурных составляющих. Для гауссовского случайного процесса эта плотность вероятности описывается выражением:
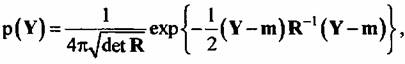
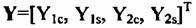 - вектор сигнала на входе двухканальной системы обработки; К - корреляционная матрица квадратурных составляющих; m - вектор математических ожиданий входных сигналов. - вектор сигнала на входе двухканальной системы обработки; К - корреляционная матрица квадратурных составляющих; m - вектор математических ожиданий входных сигналов.
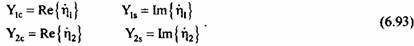
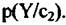
Корреляционная матрица R квадратурных составляющих имеет вид:
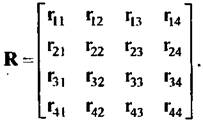
Запишем выражения для корреляционной и взаимокорреляционной функций квадратурных составляющих сигналов:
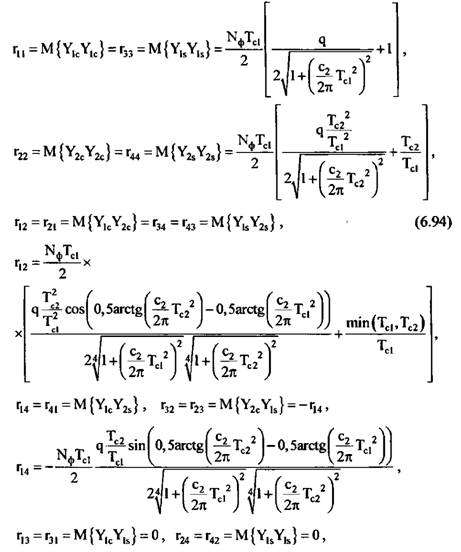
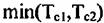 имеет вид: имеет вид:
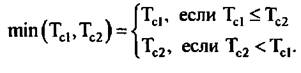
С учетом (6.94) запишем корреляционную матрицу
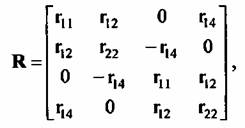
определитель которой
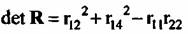
Тогда
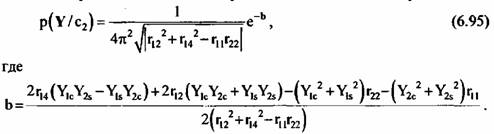
условная плотность вероятности описывается выражением:
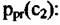

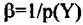 - нормирующий коэффициент. - нормирующий коэффициент.
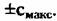
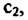 оптимальная по критерию максимума апостериорной вероятности, определяется решением уравнения оптимальная по критерию максимума апостериорной вероятности, определяется решением уравнения

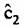 используются численные методы. используются численные методы.
С учетом (6.98) и (6.94) апостериорная плотность вероятности (6.96) принимает вид:
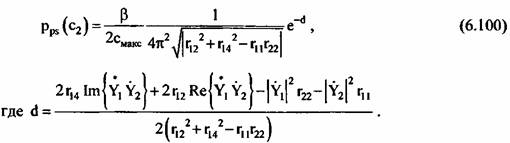
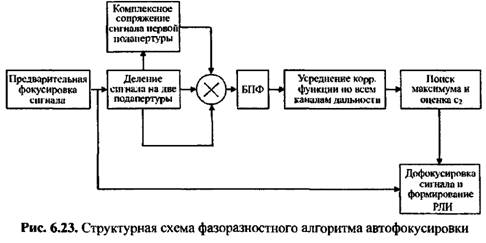
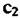 методом формирования динамического фазового портрета представлена на рис. 6.31. методом формирования динамического фазового портрета представлена на рис. 6.31.
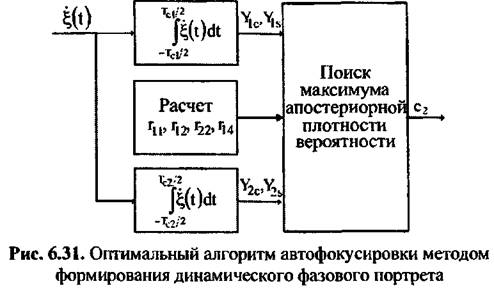
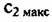 (при котором расфокусировку (при котором расфокусировку
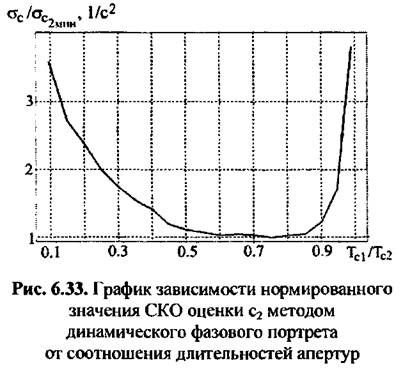
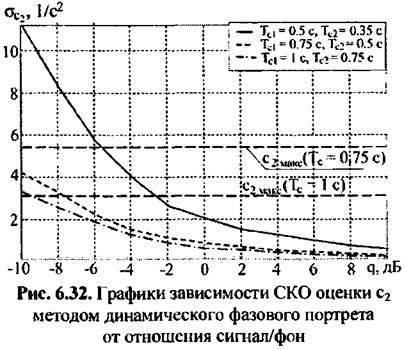
можно считать незначительной) для различных интервалов накопления.
График зависимости нормированного значения СКО оценки с 2 от соотношения между длительностями первой и второй апертур, приведенный на рис. 6.33, показывает, что оптимальное соотношение между первой и второй апертурами составляет 0,6...0,8. Эта зависимость сохраняется для всех отношений сигнал/фон, при которых работает данный алгоритм.
|