Теория систем автоматического управленияУравнения систем с нелинейностями других видов
Рассмотрим несколько примеров составления уравнений автоматических систем с нелинейностями других видов, чем в §§ 16.2 и 16.3.
Система автоматического управления с нелинейной характеристикой привода управляющего органа. Привод управляющего органа, каким бы он пи был (электрический, гидравлический, пневматический), всегда имеет, во-первых, некоторую зону нечувствительности в начале координат (рис. 16.22, а), и, во-вторых, зону насыщения. Кроме того, может иметь место еще и гистерезис (рис. 16.22, г). Эти две
криволинейные характеристики могут быть приближенно заменены кусочно-линейными (рис. 16.22, б, д или в, е, и). Наконец, существуют приводы с постоянной скоростью (рис. 16.22, ж, з), относящиеся к нелинейным звеньям релейного типа, уже рассмотренным ранее.
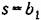 . Аналогично и в случае пневматического привода, где роль золотника играет заслонка.
 скорость перемещения управляющего органа остается постоянной
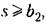 когда окна золотника пол-
ностью открыты.
Термины насыщение и гистерезис применяются здесь в обобщенном смысле для обозначения нелинейностей определенного тина; они не обязательно соответствуют физическим явлениям насыщения и гистерезиса.
Уравнение привода управляющего органа с учетом указанных обстоятельств вместо прежнего линейного будет иметь нелинейный вид:
 есть нелинейная функция задаваемая графиком (рис. 16.22, а или г). Для электрических приводов можно записать
 I
В приближенном кусочно-линейном виде (рис. 16.22,6) уравнение (16.60) записывается следующим образом:
 . Этим определяется уравнение привода управляющего органа как нелинейного звена. Уравнение линейной части составляется обычным способом в зависимости от того, в какой конкретно автоматической системе этот привод применен.
Следящая система с линейным и квадратичным трением. В § 16.3 была рассмотрена следящая система с линейным и сухим трением. Пусть теперь управляемый объект
в той же следящей системе обладает кроме линейного еще квадратичным трением, т. е. уравнение объекта имеет вид
(рис. 16.23). Тогда уравнение управляемого объекта как нелинейного звена будет
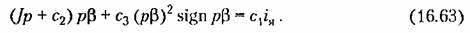
Уравнение линейной части системы в полном виде по-прежнему будет (16.53).
|
