Теория систем автоматического управленияАлгебраические способы определения автоколебаний и устойчивости в нелинейных системах первого класса
Основываясь на вышеизложенной гармонической линеаризации, составим гармонически линеаризованное уравнение всей замкнутой нелинейной автоматической системы в целом. Пусть известно дифференциальное уравнение линейной части системы

причем линейная часть может иметь структуру любой сложности (и любой порядок уравнения).
Уравнение нелинейного звена
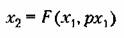
в колебательном процессе после гармонической линеаризации запишем в виде
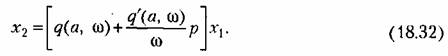
 без гистереэисной петли будет без гистереэисной петли будет

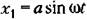 в общем в общем
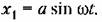 В таком виде и будем В таком виде и будем
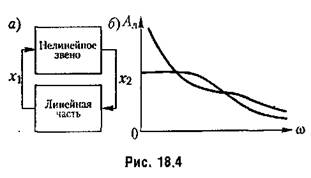
искать приближенное периодическое решение для нелинейной автоматической системы. Свойство линейной части системы, определяющее вид амплитудно-частотной характеристики типа изображенной на рис. 18.4,6, именуется свойством фильтра. Аналитическое обоснование сказанного см. в книге [72, §2.2).
Как видим, в коэффициенты уравнения (18.32) входят амплитуда а и частота со искомого колебательного процесса.
На основании уравнений (18.31) и (18.32) можно нанисать гармонически линеаризованное характеристическое уравнение замкнутой нелинейной системы в виде

с теми же особенностями в коэффициентах, что и в уравнении (18.6), описанными.
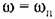 (автоколебания), коэффициенты уравнения (18.32), а значит, и коэффициенты характеристического уравнения (18.33) становятся постоянными. Вместе с тем из линейной теории известно, что появление указанных колебаний в системе при постоянных коэффициентах соответствует наличию пары чисто мнимых корней в характеристическом уравнении системы. (автоколебания), коэффициенты уравнения (18.32), а значит, и коэффициенты характеристического уравнения (18.33) становятся постоянными. Вместе с тем из линейной теории известно, что появление указанных колебаний в системе при постоянных коэффициентах соответствует наличию пары чисто мнимых корней в характеристическом уравнении системы.
 под- под-
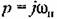
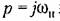 в характеристическое уравнение с постоянными коэффициентами эквивалентна отысканию границы устойчивости линейной системы. Следовательно, появление незатухающих собственных колебаний в нелинейной системе можно обнаружить применением к характеристическому уравнению (18.33) любого из методов определения границы устойчивости линейной системы, изложенных в главе 6. в характеристическое уравнение с постоянными коэффициентами эквивалентна отысканию границы устойчивости линейной системы. Следовательно, появление незатухающих собственных колебаний в нелинейной системе можно обнаружить применением к характеристическому уравнению (18.33) любого из методов определения границы устойчивости линейной системы, изложенных в главе 6.
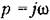 в гармонически линеаризованное характеристическое уравнение, а именно в гармонически линеаризованное характеристическое уравнение, а именно
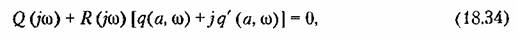
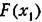 будет будет
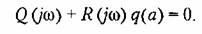
Выделим в выражении (18.34) вещественную и мнимую части:

 Это дает два уравнения: Это дает два уравнения:

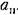
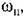 то периодические решения вообще (а значит, и автоколебания) в данной нелинейной системе невозможны. то периодические решения вообще (а значит, и автоколебания) в данной нелинейной системе невозможны.
Исследование устойчивости периодического решения дается ниже.
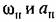 от какого-либо параметра системы, например коэффициента усиления к. Для этого нужно считать в уравнениях (18.36) параметр к переменным и записывать эти уравнения в виде от какого-либо параметра системы, например коэффициента усиления к. Для этого нужно считать в уравнениях (18.36) параметр к переменным и записывать эти уравнения в виде

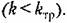
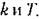 Для этого уравнения (18.36) записываются в виде Для этого уравнения (18.36) записываются в виде

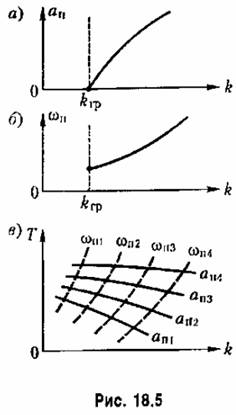
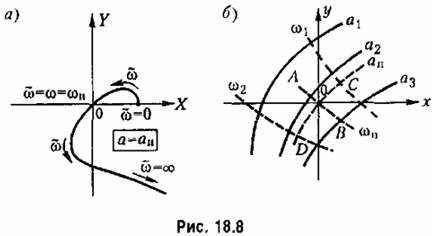
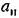 и получим для каждого из них по уравнениям (18.38) зависимости и получим для каждого из них по уравнениям (18.38) зависимости
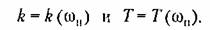
 которые также можно соединить (пунктирные кривые). которые также можно соединить (пунктирные кривые).
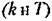 нелинейной системы. Если такие графики построить для различных возможных структурных схем системы, то можно будет выбирать также и наивыгоднейшую структурную схему проектируемой замкнутой автоматической системы с учетом нелинейностей. нелинейной системы. Если такие графики построить для различных возможных структурных схем системы, то можно будет выбирать также и наивыгоднейшую структурную схему проектируемой замкнутой автоматической системы с учетом нелинейностей.
Использование графиков коэффициентов гармонической линеаризации. Во многих задачах коэффициенты
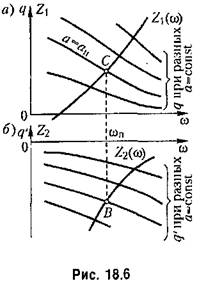
 а в ряде случаев и от частоты со. В таких случаях удобнее указанное уравнение записывать в виде а в ряде случаев и от частоты со. В таких случаях удобнее указанное уравнение записывать в виде
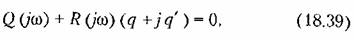
 Тогда вместо уравнений (18.36) получим для определения периодического решения уравнения: Тогда вместо уравнений (18.36) получим для определения периодического решения уравнения:
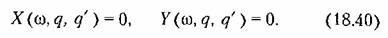
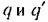 зависит сложным образом от обеих неизвестных а и со, т. е. зависит сложным образом от обеих неизвестных а и со, т. е.
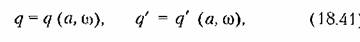 ) )
можно применить следующий прием решения.
 (рис. 18.6). Затем из уравнений (18.40) выразим (рис. 18.6). Затем из уравнений (18.40) выразим
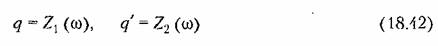
 искомого периодического решения. искомого периодического решения.
Во многих встречающихся на практике задачах вместо (18.41) будет
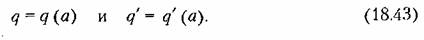
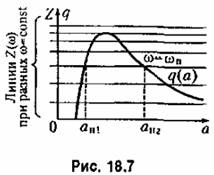
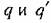 на рис. 18.6 для разных амплитуд будут иметь вид горизонтальных прямых линий. на рис. 18.6 для разных амплитуд будут иметь вид горизонтальных прямых линий.
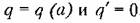 , из уравнений (18.40) можно найти , из уравнений (18.40) можно найти

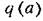 (например, на рис. 18.7 (например, на рис. 18.7
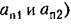 определяют в каждом случае амплитуды периодических решений. Если пересечений нет, то и периодических решений в системе не будет. В простейших случаях уравнение (18.44) решается аналитически. Графический способ. Для гармонически линеаризованного характеристического уравнения (18.33) можно определяют в каждом случае амплитуды периодических решений. Если пересечений нет, то и периодических решений в системе не будет. В простейших случаях уравнение (18.44) решается аналитически. Графический способ. Для гармонически линеаризованного характеристического уравнения (18.33) можно
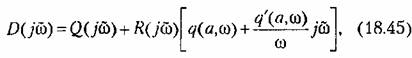
написать выражение кривой Михайлова [73]
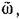 изменяющийся вдоль кривой Михайлова, от частоты (о, входящей в выражение гармонической линеаризации нелинейности. изменяющийся вдоль кривой Михайлова, от частоты (о, входящей в выражение гармонической линеаризации нелинейности.
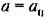 автоколебаний можно будет определить путем построения кривых автоколебаний можно будет определить путем построения кривых
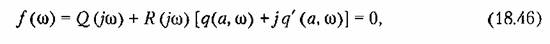
которые в общем случае не будут совпадать с кривыми Михайлова. При этом надо выбрать такое значение я, при котором кривая пройдет через начало координат.
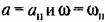 можно найти путем следующей интерполяции: можно найти путем следующей интерполяции:
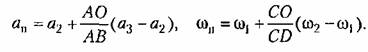
Этот способ целесообразен лишь в самых сложных случаях, когда изложенные выше способы не удается применить.
Использование коэффициентных соотношений для определения периодического решения. Для обнаружения факта наличия пары чисто мнимых корней в характеристическом уравнении (18.33) можно также применить известные алгебраические критерии устойчивости
линейных систем. Так, если гармонически линеаризованное уравнение (18.33) нелинейной системы имеет третью степень относительно p, то его можно записать в виде
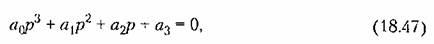
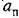 автоколебаний. автоколебаний.
Условие наличия нары чисто мнимых корней по критерию Гурвица (см. § 6.2) будет

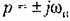 в виде в виде
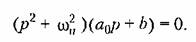
Раскрыв здесь скобки и приравняв коэффициенты этого уравнения соответствующим коэффициентам (18.47), найдем

 от одного параметра системы или на плоскости от одного параметра системы или на плоскости
двух параметров с целью их выбора.
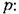
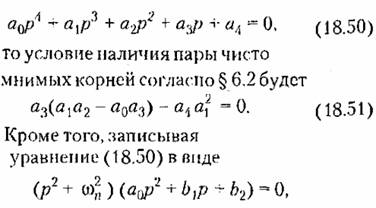
раскрывая здесь скобки и приравнивая полученные коэффициенты соответствующим коэффициентам (18.50), находим

С помощью двухуравпепий (18.51) и (18.52) решаются все вышеуказанные задачи для нелинейной системы четвертого порядка.
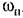 , Для систем с более сложными нелинейностями получаются два уравнения с двумя неизвестными. , Для систем с более сложными нелинейностями получаются два уравнения с двумя неизвестными.
Учет временного запаздывания в нелинейной системе. В нелинейной системе, как и в линейной, может иметься постоянное по времени запаздывание т,
При этом уравнение линейной части (18.31) получит вид

К уравнению (18.53) можно применить основной способ отыскания периодических решений или другой из изложенных выше.
|