Теория систем автоматического управленияПриближенные методы исследования устойчивости и автоколебаний
Гармоническая линеаризация нелинейностей
В этой главе будет изложен метод гармонической линеаризации для приближенного определения периодических решений (автоколебаний) и устойчивости нелинейных систем любого порядка, который по идее близок к методу эквивалентной линеаризации или методу гармонического баланса II. М. Крылова и Н. П. Боголюбова, а по результатам — также и к методу малого параметра Б. В. Булгакова.
Рассматриваемый метод является мощным средством исследования нелинейных автоматических систем в смысле простоты и довольно большой универсальности его аппарата в применении к самым разнообразным нелинейностям. Однако надо иметь в виду, что он решает задачу приближенно. Имеются определенные ограничения его применимости, о которых будет сказано ниже. Эти ограничения обычно хорошо соблюдаются в задачах теории автоматического управления. Практические расчеты и эксперимент показывают приемлемость этого метода для многих видов нелинейных систем.
Пусть дано какое-нибудь нелинейное выражение вида

что означает отсутствие постоянной составляющей в данном разложении.
В настоящей главе будет везде предполагаться выполнение условия отсутствия постоянной составляющей (18.5). Впоследствии будет дан метод исследования автоколебаний при наличии постоянной составляющей.
Если принять во внимание, что из (18.2) и (18.3)

то формулу (18.4) при условии (18.5) можно будет записать в виде
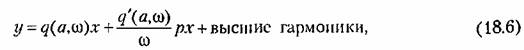
 — коэффициенты гармонической линеаризации, определяемые формулами: — коэффициенты гармонической линеаризации, определяемые формулами:

 заменяется выражением (18.6), заменяется выражением (18.6),
 постоянны постоянны
 изменяются изменяются
(см. гл. 20). Для разных амплитуд и частот периодических процессов коэффициенты выражения (18.6) будут различны по величине. Это очень важное для дальнейшего обстоятельство является существенным отличием гармонической линеаризации но сравнению с обычным способом линеаризации (§ 3.1), приводящим к чисто линейным выражениям, которые применялись в предыдущих разделах книги. Указанное обстоятельство и позволит путем применения к выражению (18.6) линейных методов исследования проанализировать основные свойства нелинейных систем, которые не могут быть обнаружены при обычной линеаризации.

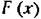 не имеет гистерезисной петли (рис. 16.8, б, рис. 16.22, а и др.). не имеет гистерезисной петли (рис. 16.8, б, рис. 16.22, а и др.).
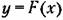 после гармонической линеаризации после гармонической линеаризации
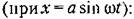

при условии отсутствия постоянной составляющей:

 будет будет
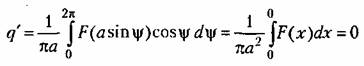
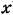
Следовательно, при отсутствии гистерезисной петли нелинейное выражение (18.8) заменяется более простым:

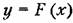 с точностью до высших с точностью до высших
гармоник заменяется прямолинейной, тангенс угла наклона которой q зависит от амплитуды колебаний а. Другими словами, нелинейное звено уподобляется линейному с передаточным числом (коэффициентом передачи), зависящим от амплитуды а колебаний входной величины х,
 , Таким образом, нелинейное отставание по координате в виде гистерезисной петли превращается при гармонической линеаризации в эквивалентное линейное отставание по фазе. , Таким образом, нелинейное отставание по координате в виде гистерезисной петли превращается при гармонической линеаризации в эквивалентное линейное отставание по фазе.
Можно создать специальное нелинейное звено с опережающей петлей, что будет эквивалентно линейному опережению фазы при введении производной, но с тем отличием, что величина опережения фазы будет зависеть от амплитуды колебаний, чего нет в линейных системах.
В случаях, когда нелинейное звено описывается сложным уравнением, включающим сумму различных линейных и нелинейных выражений, каждый из нелинейных членов подвергается гармонической линеаризации по отдельности. Произведение же нелинейностей рассматривается обязательно в целом как одна сложная нелинейность, При этом могут встретиться иного характера нелинейные функции.
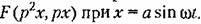 В этом случае получаем В этом случае получаем

при условии

 и и

 можно получить удвоением интеграла (0, тт.), т. с. можно получить удвоением интеграла (0, тт.), т. с.

а для симметричных относительно начал а координат безгистерезисных характеристик Р(х) при вычислении q (а) можно писать

Приведем выражения для коэффициентов некоторых простейших нелинейных звеньев. Затем их можно будет непосредственно исиользоватьпри решении различных конкретных задач.
 Как частные случаи будут получены уравнения других типов релейных звеньев. Как частные случаи будут получены уравнения других типов релейных звеньев.
 согласно согласно
 то переключения реле то переключения реле
происходят в точках A, В, С, D (рис. 18.1, б), в которых имеем

Следовательно, после использования свойств (18.12) каждый из интегралов (18.10) разбивается на три слагаемых:
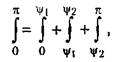
причем первое и третье из них согласно рис. 18.1, а и б будут нулями. Поэтому выражения (18.10) принимают вид

 Рассмотрим частные случаи. Рассмотрим частные случаи.
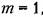 , из выше написанных формул получаем , из выше написанных формул получаем
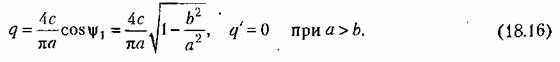
 , имеем , имеем

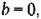 находим находим

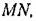 приблизительно заменяющая ломаную АВСО. приблизительно заменяющая ломаную АВСО.


 при производной согласно (18.17) тоже уменьшается с увеличением амплитуды а колебаний входной величины, что и попятно, так как эффект влияния гистерезисиой петли на процесс колебаний в релейном звене должен быть тем меньше, чем больше амплитуда колебаний по сравнению с шириной гистерезисиой петли. при производной согласно (18.17) тоже уменьшается с увеличением амплитуды а колебаний входной величины, что и попятно, так как эффект влияния гистерезисиой петли на процесс колебаний в релейном звене должен быть тем меньше, чем больше амплитуда колебаний по сравнению с шириной гистерезисиой петли.
Коэффициенты гармонической линеаризации других простейших нелинейных звеньев. Рассмотрим пелинейпоезвеноезоной нечувствительности и с насыщением (рис. 18.2, а). Согласно рис. 18.2, б, где
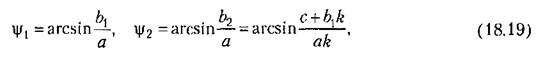
интеграл (18.10) на участке (0, я) разбивается на пять слагаемых, причем два из них равны нулю. Поэтому
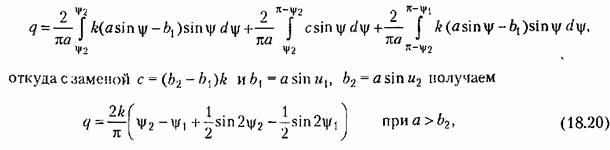

 определяются формулами (18.19). Ввиду отсутствия гистерезисной петли определяются формулами (18.19). Ввиду отсутствия гистерезисной петли
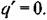
 определяется выражением (18.20). определяется выражением (18.20).
Как частный случай отсюда получается значение ц (а) для звена с зоной нечувствительности без насыщения (рис. 18.2, в). Для этого в предыдущем решении нужно
 Тогда Тогда
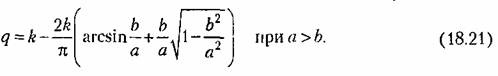
 усиления значительно при малых амплитудах и невелико при больших, причем усиления значительно при малых амплитудах и невелико при больших, причем
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
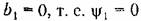 , из (18.20) и (18.19) получаем , из (18.20) и (18.19) получаем

 (линейная характеристика). При амплитудах (линейная характеристика). При амплитудах
 , чем больше амплитуда (в противоположность предыдущему). , чем больше амплитуда (в противоположность предыдущему).
Для звена с переменным коэффициентом усиления согласно рис. 18.2, д и е но формуле (18.10) с учетом (18.12) получаем


Для нелинейного звена с насыщением и с гистерезисной петлей (рис. 18.3, а) уравнение получит вид (18.9), где согласно рис. 18.3, б и формулам (18.10)

 то в процессе колебаний не будет захватываться зона насыщения и получится чисто гистерезисная характеристика (рис. 18.3, в). В данном случае то в процессе колебаний не будет захватываться зона насыщения и получится чисто гистерезисная характеристика (рис. 18.3, в). В данном случае
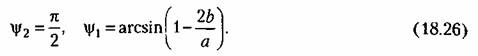
Уравнение звена с гистерезисной характеристикой вида рис. 18.3, в поэтому будет иметь форму (18.9), где согласно (18.24)
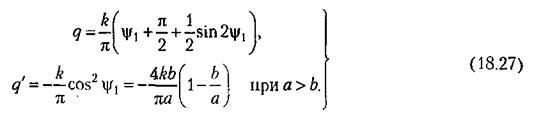
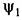 вычисляется по формуле (18.26). вычисляется по формуле (18.26).
Такого же типа характеристика (рис. 18.3, в) получалась и для чувствительного элемента с сухим трением в системе стабилизации давления, рассмотренной в § 16 (см. рис. 16.21,6), когда мы пренебрегали массой. Следовательно, для такого нелинейного звена с сухим трением будут справедливы те же формулы (18.27) с заменой в них только

а уравнение (16.58) для колебательного процесса в форме (18.9) будет
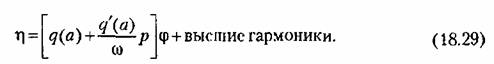
Этого же типа характеристика (рис. 18.3, в) имела место и для нелинейного звена с зазором в следящей системе (см. рис. 16.20, б), причем там к = 1. Следовательно, уравнение (16.55) данного нелинейного звена (для колебательного процесса) запишется в виде
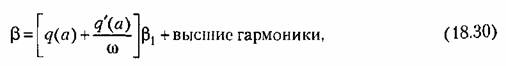

Для пелинейностей, не заданных аналитически, существует графический способ определения q (а) (см. § 3.8 в книге [72]).
|