Теория систем автоматического управленияНелинейные системы второго класса
Нелинейные системы второго класса - это системы с несколькими нелинейными звеньями или же с одним нелинейным звеном, когда под знаки нелинейных функций входят две или более переменных, связанных между собой линейными передаточными функциями или нелинейными уравнениями. Обычный прием приближенного решения, излагаемый ниже в примерах 1 -3, справедлив при соблюдении условия фильтра, оговоренного в § 18.2, для всех передаточных функций, связывающих указанные неременные. Если это условие не соблюдается, применяется специальный прием решения, изложенный ниже в примере 4.
Пример 1. В предыдущем параграфе рассматривалось влияние нелинейности привода, а затем влияние квадратичного трения по отдельности. Рассмотрим теперь
 как в уравнении как в уравнении
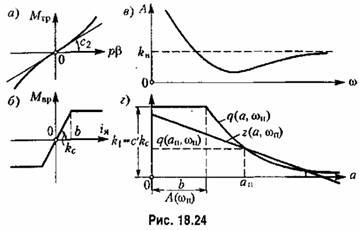
(18.90), или, что то же самое, графиком на рисунке 18.24, а. Нелинейный привод пусть имеет характеристику типа насыщения (рис. 18.24, б).
(18,90) примет вид
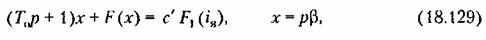
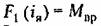 и определяется графиком рис. 18.24,6. и определяется графиком рис. 18.24,6.
В данном случае получается нелинейная система второго класса Приближенно полагаем, что при автоколебаниях

 ~ — модуль и аргумент амплитудно-фазовой характеристики линейной ~ — модуль и аргумент амплитудно-фазовой характеристики линейной
части, получаемой из уравнения (18.67), которое согласно (18.129) надо умножить на p. В результате получим
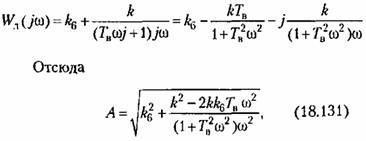
что изображено графически на рис. 18.24, в.
 входят раздельно, то и входят раздельно, то и

гармоническую линеаризацию можно производить для каждой из них отдельно. К нелинейности в левой части уравнения (18.129) применяем формулы из прежнего примера 3 (с квадратичным трением), а к нелинейности в правой части — формулы (18.65) и (18.66), в которых, в соответствии с (18.130), вместо а подставляем Аа. В результате нелинейное уравнение (18.129) принимает вид
где

причем Л (со) определяется формулой (18.131) или графиком рис. 18.24, в.
Из уравнений (18.132) и (16.53) получаем гармонически линеаризованное характеристическое уравнение замкнутой системы в виде
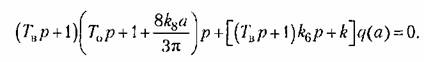
 находим: находим:
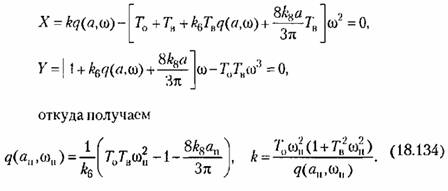
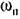 следующим образом. следующим образом.
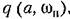 показанную на рис.18.24, г. показанную на рис.18.24, г.
 ): ):
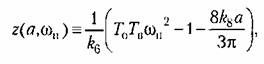
 . В точках . В точках
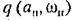 После этого по второй из формул (18.134) подсчитаем величину параметра к. После этого по второй из формул (18.134) подсчитаем величину параметра к.
 При этом согласно (18.134) При этом согласно (18.134)
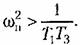
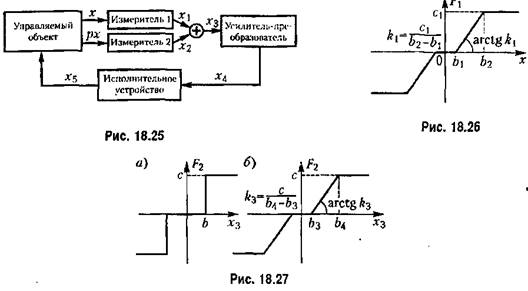
Пример 2. Пусть в системе, функциональная схема которой изображена на рис.
18.25, управляемый объект описывается уравнением

измеритель 1 — нелинейный (рис. 18.26) —

измеритель 2 — линейный —

линейный усилитель-преобразователь вместе с линейным исполнительным устройством —

 задана в двух вариантах, обусловленных разными задана в двух вариантах, обусловленных разными
режимами работы исполнительного устройства — релейным (рис. 18.27, а) или непрерывным (рис. 18.27, б).
Будем определять автоколебания приближенно в виде

 входящими под знаки нелинейностей, со- входящими под знаки нелинейностей, со-
гласно рис. 18.25 идет через нелинейное звено. Следовательно, данная система является системой второго класса (с двумя нелинейными звеньями).
Гармоническая линеаризация нелинейностей согласно § 18.1 дает

и для двух вариантов исполнительного устройства соответственно
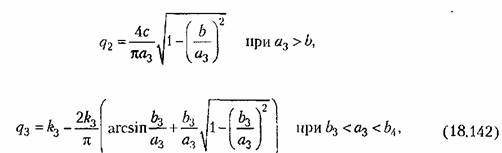
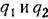 ). ).
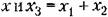 запишется теперь согласно (18.136), (18.137) и (18.140) в виде запишется теперь согласно (18.136), (18.137) и (18.140) в виде
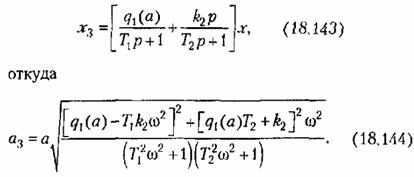
 будет далее использовано. будет далее использовано.
Составим теперь характеристическое уравнение всей замкнутой системы в гармонически линеаризованном виде. Согласно (18.135)—(18.140) получаем

Пренебрегая произведениями постоянных времени при высших степенях;? по сравнению с их суммой, что вполне допустимо при рассмотрении низкочастотных автоколебаний (которые здесь и будут иметь место), запишем характеристическое уравнение в виде

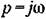 дает: дает:

 по сравнению с единицей) по сравнению с единицей)

 но сравнению с единицей, найдем но сравнению с единицей, найдем

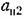 (неустойчивое). (неустойчивое).
 при заданном значении (18.146), что после пренебрежения прежними малыми членами дает при заданном значении (18.146), что после пренебрежения прежними малыми членами дает

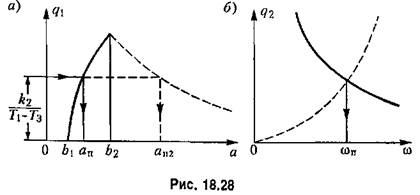
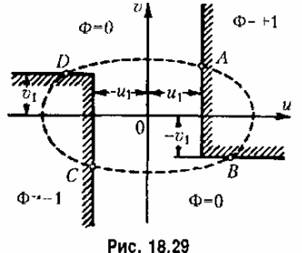
 берется из графика рис. 18.28, а. берется из графика рис. 18.28, а.
 (сплошная кривая на рис. 18.28, б). На тот же график наносим правую часть уравнения (18.145) (пунктирная кривая на (сплошная кривая на рис. 18.28, б). На тот же график наносим правую часть уравнения (18.145) (пунктирная кривая на

Пример 3. Рассмотрим систему, в которой нелинейным звеном является логическое устройство (рис. 16.25) с простейшим законом формирования сигнала управления (рис. 16.26). Уравнения системы заданы в виде (16.66)—(16.69).
Установившийся режим в такой системе будет автоколебательным. Искать его будем приближенно в синусоидальной форме

так как свойство фильтра в данной системе соблюдается. Тогда величины и и V будут

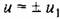 , т. е. в , т. е. в
 рис. 18.29). рис. 18.29).
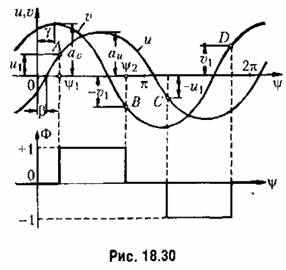
 изображен на изображен на
рис. 18.30.
 .причем .причем
Отсюда
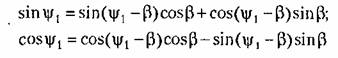
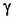 ). Учитывая, что согласно (18.149) ). Учитывая, что согласно (18.149)
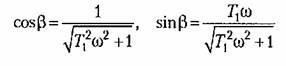
 ), находим ), находим

Теперь по правилам § 18.1 легко записать результат гармонической линеаризации нелинейной логической функции:
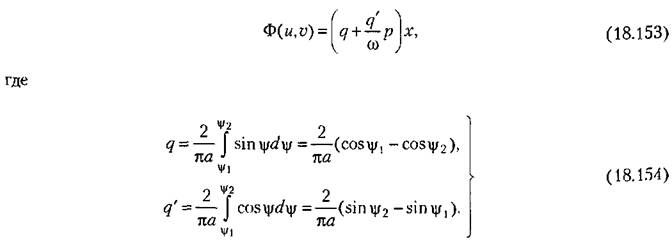
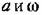 (амплитуды и частоты автоколебаний переменной). (амплитуды и частоты автоколебаний переменной).
Характеристическое уравнение рассматриваемой системы в целом после указанной гармонической линеаризации нелинейности, согласно (16.66)-( 16.69) и (18.153), принимает вид
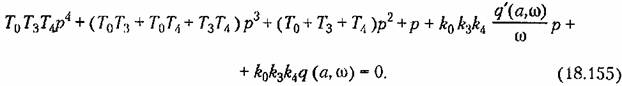
 Получаем вещественную и мнимую части соответственно Получаем вещественную и мнимую части соответственно
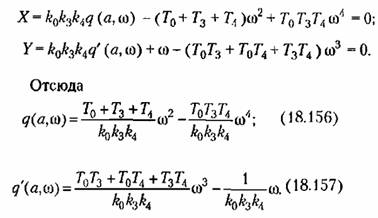
 (рис. 18.31, а). Затем на первом из них наносится (рис. 18.31, а). Затем на первом из них наносится
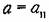 и и

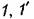 па рис. 18.31, а. па рис. 18.31, а.
 из уравнении (18.156) и (18.157), находим из уравнении (18.156) и (18.157), находим

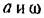 и вычисляя каждый раз по этим и вычисляя каждый раз по этим
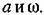
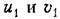 (см. (см.
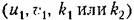 . При этом нужно . При этом нужно
учитывать, что из требования вещественности выражений (18.151) и (18.152) следует выбирать
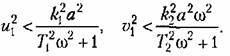
Пример 4. Рассмотрим систему автоматического управления с двумя нелинейностями в случае, когда их гармоническая линеаризация по отдельности невозможна вследствие отсутствия свойства фильтра у звена, стоящего между ними (рис. 18.32).
Представим весь блок, включающий обе нелинейности, изображенный отдельно на рис. 18.33, как одно нелинейное звено. По отношению
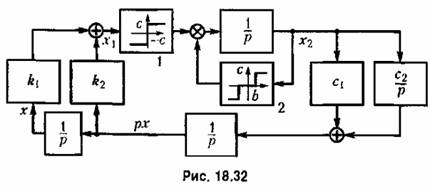
к нему система обладает свойством фильтра. Следовательно, автоколебания в системе можно искать приближенно в виде

Система уравнений, описывающих работу всей системы, имеет вид

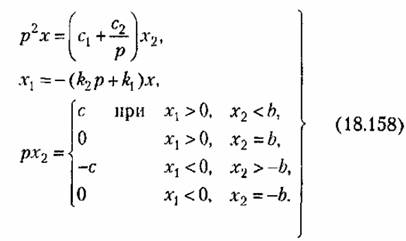
 определяется соотношением определяется соотношением

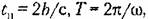 получаем получаем

Для того чтобы выходной сигнал достигал уровня ограничения (т. е. чтобы вторая нелинейность участвовала в работе), необходимо выполнение условия
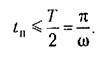
Таким обрезом, следует рассматривать входные сигналы с частотой

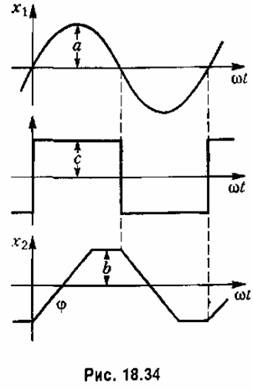
Амплитуда первой гармоники для треугольного сигнала с ограничением имеет вид
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение

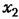 будет будет
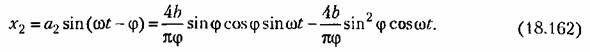
В результате можно записать уравнение нелинейного блока (рис. 18.33) в гармонически линеаризованном виде:
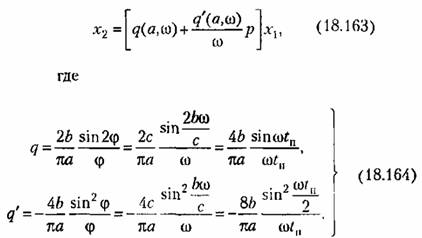
Характеристическое уравнение всей замкнутой системы при этом получит вид

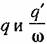 в виде в виде

 (18.165), что дает: (18.165), что дает:
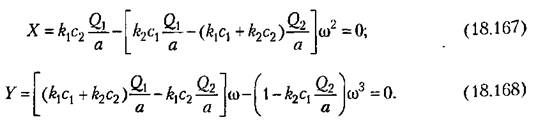
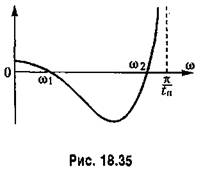
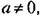 из (18.167) можно найти частоту со,,: из (18.167) можно найти частоту со,,:

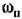 под знаком тригонометрических функций, решаем это уравнение графически. Его левая часть изображается кривой, показанной на рис. 18.35. под знаком тригонометрических функций, решаем это уравнение графически. Его левая часть изображается кривой, показанной на рис. 18.35.

Преобразуем уравнение (18.168) к виду

 сигнала на входе нелинейного звена. Остается определить, которое из двух найденных решений соответствует действительным автоколебаниям в системе. Для этого исследуем устойчивость найденного решения с помощью критерия (18.63). сигнала на входе нелинейного звена. Остается определить, которое из двух найденных решений соответствует действительным автоколебаниям в системе. Для этого исследуем устойчивость найденного решения с помощью критерия (18.63).
Поскольку согласно (18.167)

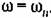
 представим Y в виде представим Y в виде

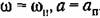 , а частная производная , а частная производная
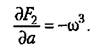
В результате условие устойчивости колебаний (18.63) сводится к требованию

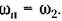 Таким образом, в системе существуют автоколебания, параметры которых Таким образом, в системе существуют автоколебания, параметры которых

Помимо условия (18.171) для устойчивости найденного решения необходимо, чтобы все коэффициенты характеристического уравнения (18.165) были положительными, а именно:
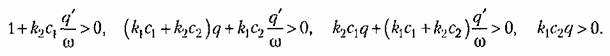
Легко проверить, что все эти условия были выполнены в самом процессе отыскания периодического решения.
|