Теория систем автоматического управленияВычисление высших гармоник и уточнение первой гармоники автоколебаний
Пусть задано дифференциальное уравнение нелинейной системы
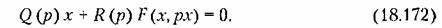
До сих пор периодическое решение (автоколебания) для нелинейной системы искалось для первого приближения в виде

что соответствовало приближенному значению первой гармоники периодического решения. Все высшие гармоники при этом отбрасывались ввиду их малости при наличии в системе свойства фильтра (§18.2).
 гармоники: гармоники:
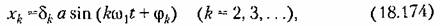
 гармоники. гармоники.
Теперь с учетом конечного числа п высших гармоник искомое периодическое решение запишется в виде

где
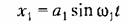
обозначает уточненную по сравнению с (18.173) первую гармонику автоколебаний.
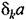 несущественные малые высшего порядка, но зато привело бы к неразрешимой системе уравнений. несущественные малые высшего порядка, но зато привело бы к неразрешимой системе уравнений.
 мало отличается от синусоидального (18.173), будем для определения высших гармоник, порождаемых нелинейностью (т. е. на выходе нелинейного звена, где они немалые), подавать па вход нелинейного звена синусоиду (18.173). мало отличается от синусоидального (18.173), будем для определения высших гармоник, порождаемых нелинейностью (т. е. на выходе нелинейного звена, где они немалые), подавать па вход нелинейного звена синусоиду (18.173).
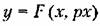 в в
комплексной форме запишется в виде
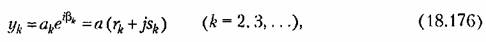
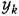 на выходе нелинейного звена, а -- амплитуда входной синусоиды. на выходе нелинейного звена, а -- амплитуда входной синусоиды.
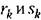 определяются коэффициентами ряда Фурье, деленными определяются коэффициентами ряда Фурье, деленными
пай, т. е.
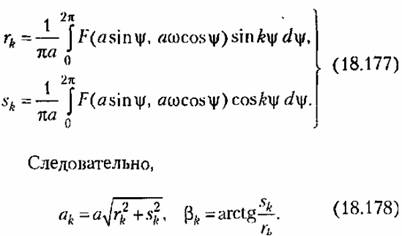 I I
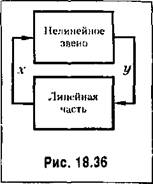
Затем эти немалые высшие гармоники с выхода нелинейного звена проходят через линейную часть (рис. 18.36) с передаточной функцией
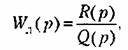
становясь малыми за счет наличия свойства фильтра.
Учитывая перемену знака воздействия в замкнутой системе, получаем малые высшие гармоники для переменной х в виде (18.174), где

Итак, по формулам (18.179) легко определяются относительная амплитуда и фаза каждой из высших гармоник (18.174) периодического решения (автоколебаний) для переменной х (18.175). Они вычисляются но известным амплитуде а и частоте со первого приближения (18.173), определению которого были посвящены предыдущие параграфы данной главы.
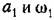
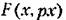 в ряд Тейлора: в ряд Тейлора:
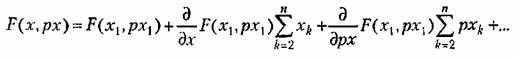
Применяя далее разложение в ряд Фурье, по аналогии с § 18.1 получим
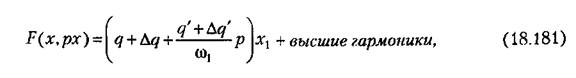
 ) )
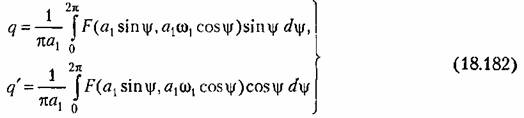
и новые добавки к ним, вычисляемые, в отличие от этих основных, через первое приближение (18.173):
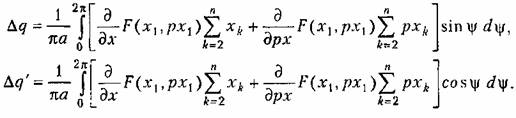
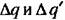 с учетом (18.174) можно преобразовать к следующей, удобной для вычислений, форме: с учетом (18.174) можно преобразовать к следующей, удобной для вычислений, форме:
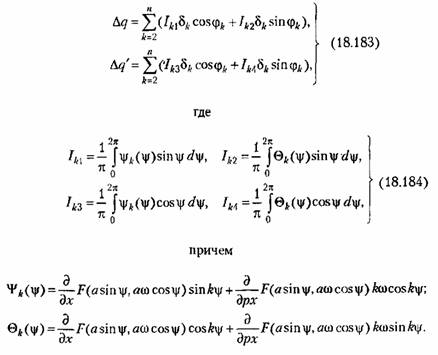
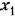 в виде в виде

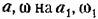
Итак, полностью найдено искомое уточненное решение для автоколебаний (18.175) в виде
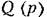 некоторыми добавками к его коэффициентам и определяемый но формуле (18.186). некоторыми добавками к его коэффициентам и определяемый но формуле (18.186).
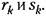
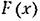 наиболее существенной из высших гармоник будет третья. Учитывая ее, представляем искомое периодическое решение (автоколебания), согласно (18.175), в виде наиболее существенной из высших гармоник будет третья. Учитывая ее, представляем искомое периодическое решение (автоколебания), согласно (18.175), в виде
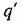 и характеристическое уравнение будет и характеристическое уравнение будет
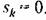 , В результате приходим к весьма простым соотношениям: , В результате приходим к весьма простым соотношениям:
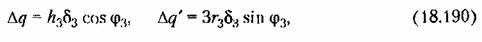
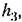 причем причем
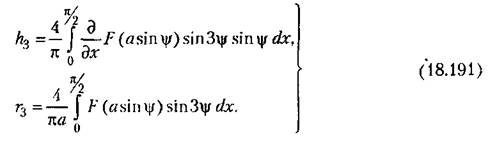
Из формул (18.179) определяются относительная амплитуда и фаза третьей гармоники:
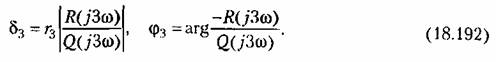
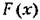 с учетом третьей гармоники в виде с учетом третьей гармоники в виде
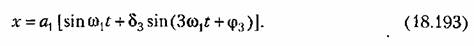
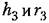 по формулам (18.191) для релейных по формулам (18.191) для релейных
характеристик, где оно представляет некоторые особенности.
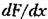 будет для этой будет для этой
 , где она равна мгновенному , где она равна мгновенному
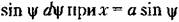 можно преобразовать к виду можно преобразовать к виду
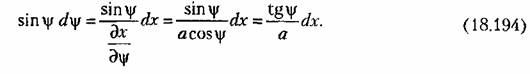
 , то эту формулу в данном примере можно переписать в виде , то эту формулу в данном примере можно переписать в виде
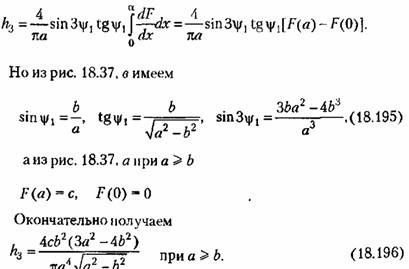
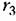 согласно рис. 18.37, г принимает вид согласно рис. 18.37, г принимает вид
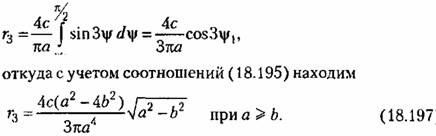
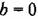 , получим: , получим:

Рассмотрим два примера, иллюстрирующих процесс отыскания высших гармоник при автоколебаниях, а также уточнения первой гармоники за счет учета низших.
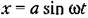 уже были найдены ранее, в примере 1 § 18.3, в общем виде. уже были найдены ранее, в примере 1 § 18.3, в общем виде.
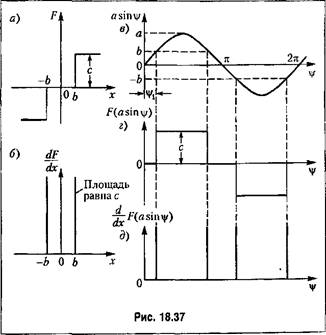
Пусть теперь заданы параметры системы:
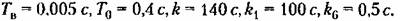
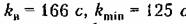 :. :.
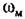 рис. 18.14, б). рис. 18.14, б).
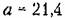 в, что практически можно считать неустойчивостью системы в большом. Поэтому уточнение решения с вычислением высших гармоник произведем только для первого периодического решения. в, что практически можно считать неустойчивостью системы в большом. Поэтому уточнение решения с вычислением высших гармоник произведем только для первого периодического решения.
Для данной нелинейности (рис. 18.13, а) но формулам (18.191) находим выражения:
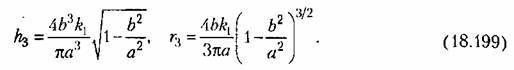
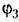 третьей гармоники в виде третьей гармоники в виде
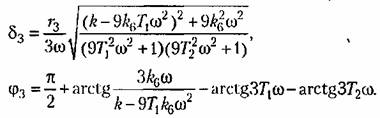
Вычисление по этим формулам дает
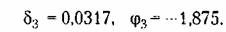
Для уточнения первой гармоники за счет только что вычисленной третьей гармоники находим согласно (18.190) добавки к коэффициентам гармонической линеаризации:
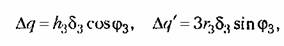
подставляя которые в (18.188) согласно (18.68) придем к уточненному характеристическому уравнению
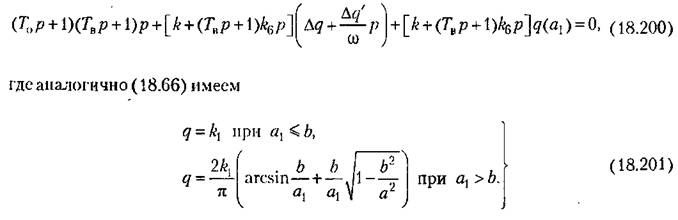
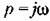 и выделив вещественную и мнимую части, и выделив вещественную и мнимую части,
получим два уравнения:
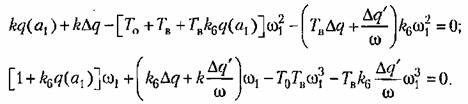
Эти уточненные уравнения отличаются от прежних уравнений первого приближения несколькими добавочными членами, но способ решения их остается прежним. Из последнего уравнения находим
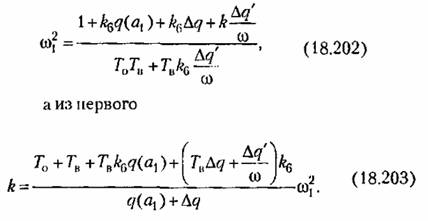
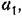 первой гармоники периодического решения. первой гармоники периодического решения.
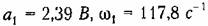 Значения эти достаточно близки к величинам первого приближения, а подсчитанная выше амплитуда третьей гармоники достаточно мала. Значения эти достаточно близки к величинам первого приближения, а подсчитанная выше амплитуда третьей гармоники достаточно мала.
Пример 2. Пусть в системе автоматического управления используется двухфазный двигатель, описываемый нелинейным уравнением (18.119). В примере 7 § 18.3 найдены автоколебания для первого приближения в общем виде. Рассмотрим следующий числовой пример;
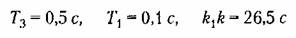
с двумя вариантами нелинейности:
а) слабая нелинейность
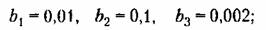
б) сильная нелинейность
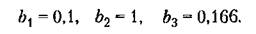
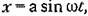 где для варианта слабой нелинейности где для варианта слабой нелинейности
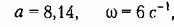
а для варианта сильной нелинейности
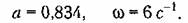
 подсчитанные по формулам (18.177), оказываются нулями. Поэтому остается только третья гармоника, для которой но формулам (18.177) для данной нелинейности с учетом обозначений (18.121) находим: подсчитанные по формулам (18.177), оказываются нулями. Поэтому остается только третья гармоника, для которой но формулам (18.177) для данной нелинейности с учетом обозначений (18.121) находим:

При указанных выше данных получаем для варианта слабой нелинейности
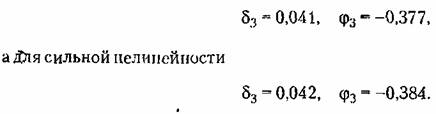
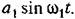 Для этого по Для этого по
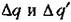 к коэффициентам гармонической линеаризации: к коэффициентам гармонической линеаризации:
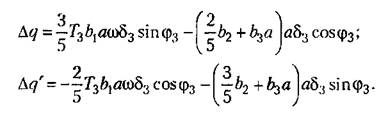
Поэтому новое характеристическое уравнение для определения уточненной первой гармоники будет
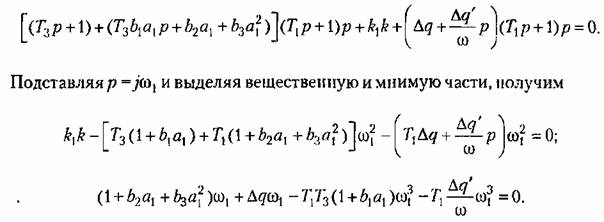
Эти уравнения решаются тем же методом, что и (18.125), а именно: из второго
уравнения получаем
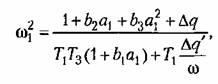
а из первого,
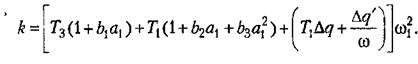
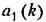 вида рис. 18.23, в. вида рис. 18.23, в.
Для приведенных выше числовых значений параметров системы получаем следующие уточненные значения амплитуды и частоты автоколебаний: - для слабой нелинейности
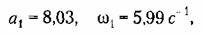
Для сильной нелинейности
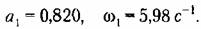
Как видим, сильная нелинейность1 значительно снижает амплитуду автоколебаний (в линейной системе было бы а1 Этот результат получался выше в решении по первому приближению и подтверждается теперь уточненным решением.
|