Теория систем автоматического управленияУчет временного запаздывания в реле
 заданы постоянными, т. е. считалось, что характеристики реле имеют обычный гистерезисный вид с заданным по входной координате отставанием в срабатывании реле. Теперь же будем считать, что имеются данные запаздывания во времени срабатывания и отпускания реле (одинаковые). Такое нелинейное звено с запаздыванием можно разбить на два элемента: 1) обычное нелинейное звено, характеризующееся графиком рис. 18.45, б или в, и 2) элемент запаздывания (рис. 18.45, а), описываемый уравнением заданы постоянными, т. е. считалось, что характеристики реле имеют обычный гистерезисный вид с заданным по входной координате отставанием в срабатывании реле. Теперь же будем считать, что имеются данные запаздывания во времени срабатывания и отпускания реле (одинаковые). Такое нелинейное звено с запаздыванием можно разбить на два элемента: 1) обычное нелинейное звено, характеризующееся графиком рис. 18.45, б или в, и 2) элемент запаздывания (рис. 18.45, а), описываемый уравнением

Тогда можно будет записать выражение амплитудно-фазовой характеристики линейной части системы вместе с элементом запаздывания в виде
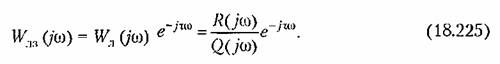
Правило построения такой характеристики описано в главе 6.
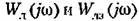 , изображенные на рис. 18.45, г, а также прямую , изображенные на рис. 18.45, г, а также прямую
 пересекаются, то будут иметь место автоколебания. Но, как видно из рис. 18.45, г, при достаточно малых запаздываниях т указанные кривые могут не пересекаться, т. е. автоколебаний не будет. пересекаются, то будут иметь место автоколебания. Но, как видно из рис. 18.45, г, при достаточно малых запаздываниях т указанные кривые могут не пересекаться, т. е. автоколебаний не будет.
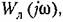 в которой в которой
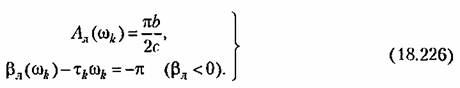
 , и из второго — критическое время запаздывания: , и из второго — критическое время запаздывания:
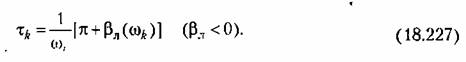
 или же аналитически, используя выражение (18.220). или же аналитически, используя выражение (18.220).
 . Поэтому выгодно, чтобы временное запаздывание в реле, рассматриваемое здесь, было бы сравнительно малым, а зона нечувствительности имела бы большую величину (но не превышала допустимых значений, полученных из статического расчета точности регулирования). . Поэтому выгодно, чтобы временное запаздывание в реле, рассматриваемое здесь, было бы сравнительно малым, а зона нечувствительности имела бы большую величину (но не превышала допустимых значений, полученных из статического расчета точности регулирования).
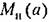 имеются два значения а. Это следует из графика рис. 18.40, а, причем на основании (18.16) имеем имеются два значения а. Это следует из графика рис. 18.40, а, причем на основании (18.16) имеем



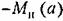 , что и даст нам точку О (величина запаздывания т задана, со,, неизвестна). Условие для определения со,, будет , что и даст нам точку О (величина запаздывания т задана, со,, неизвестна). Условие для определения со,, будет

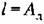 , а затем амплитуда автоколебаний ап2 по графику рис. 18.45, д. , а затем амплитуда автоколебаний ап2 по графику рис. 18.45, д.
В заключение заметим, что при исследовании нелинейных автоматических систем применяются также приближенные методы Б. В. Булгакова (см. [17] или [701), которые здесь не излагаются.
|