Теория систем автоматического управленияСистема автоматической стабилизации температуры
Уравнения системы с релейным звеном были описаны в примере 5 § 18.3. Выражение амплитудно-фазовой характеристики линейной части системы с добавлением жесткой обратной связи будет
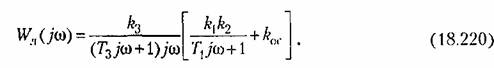
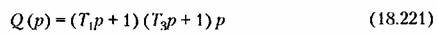
не имеет корней с положительной вещественной частью, а нулевой корень говорит о том, что линейная часть системы нейтральна.
 (рис. 18.43, б). (рис. 18.43, б).
Множитель перед квадратной скобкой (18.220) соответствует инерционному интегрирующему звену (привод с управляющим органом). Он изображен на рис. 18.43, е.

 пересекаются, а введением пересекаются, а введением

 на рис. 18.43, г) можно было бы уничтожить автоколебания замкнутой нелинейной системы и без обратной связи. Напротив, неудачный выбор параметров может привести к автоколебаниям системы даже и при наличии жесткой обратной связи, если на рис. 18.43, д кривые пересекутся. Чем меньше гистсрезисная петля (рис. 18.20, а), тем больше будет т (рис. 18.39) и тем легче, как видно из рис. 18.39, б и рис. 18.43, г, д, сделать замкнутую систему устойчивой. на рис. 18.43, г) можно было бы уничтожить автоколебания замкнутой нелинейной системы и без обратной связи. Напротив, неудачный выбор параметров может привести к автоколебаниям системы даже и при наличии жесткой обратной связи, если на рис. 18.43, д кривые пересекутся. Чем меньше гистсрезисная петля (рис. 18.20, а), тем больше будет т (рис. 18.39) и тем легче, как видно из рис. 18.39, б и рис. 18.43, г, д, сделать замкнутую систему устойчивой.
 в прямую (пунктир на рис. 18.43, д), в прямую (пунктир на рис. 18.43, д),
причем добиться уничтожения автоколебаний в этом случае нельзя, а можно бороться лишь за уменьшение их амплитуды.
 примет очертание, показанное пунктиром (рис. 18.43, е). Введение же жесткой обратной связи, как видно из рис. 18.43, ж, полностью уничтожает автоколебания. примет очертание, показанное пунктиром (рис. 18.43, е). Введение же жесткой обратной связи, как видно из рис. 18.43, ж, полностью уничтожает автоколебания.
Из этого предварительного рассмотрения можно сделать вывод, во-первых, о важном стабилизирующем свойстве дополнительной жесткой обратной связи в системе и, во-вторых, о стабилизирующем свойстве зоны нечувствительности реле. С точки зрения устойчивости системы выгодно увеличивать и то, и другое. Однако эти возможности ограничены из-за увел и дення статической ошибки системы при усилении жесткой обратной связи и при увеличении зоны нечувствительности реле. Последнее связано с тем, что система может находиться в состоянии равновесия в любой точке зоны нечувствительности; получается не одно определенное состояние равновесия, а целая область возможных состояний равновесия с разными значениями управляемой величины.
После сделанных предварительных заключений перейдем к определению амплитуды и частоты автоколебаний в тех случаях, когда последние имеют место.
В случае идеальной релейной характеристики в соответствии с (18.211) и (18.18)
имеем

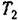 ). ).
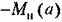 до точки пересечения, причем с учетом (18.222) получаем до точки пересечения, причем с учетом (18.222) получаем

где /берется из графика или вычисляется но формуле
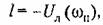
 находится из условия находится из условия


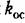 ==0, т. е. ==0, т. е.
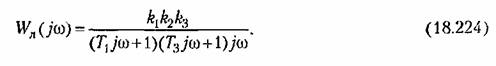
 увеличивается амплитуда автоколебаний. увеличивается амплитуда автоколебаний.
Для характеристики реле в виде рис, 18.20, а поведение системы без жесткой обратной связи поясняется рис. 18.44, б. Здесь автоколебания могут отсутствовать (кривая 1 рис. 18.44, б) возможно одно периодическое решение (кривые 2 и 3, пересекающиеся в точке В) или два периодических решения (кривые 2 и 4, пересекающиеся в точках А и С). При этом кривая 3 соответствует меньшим, а кривая 4 — большим значениям т в релейной характеристике (см. рис. 18.39). Точки В и Л отвечают
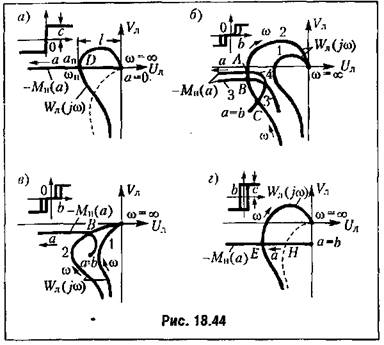
 в большом. Величины амплитуды и частоты автоколебаний определяются по самим кривым в точках их пересечения. в большом. Величины амплитуды и частоты автоколебаний определяются по самим кривым в точках их пересечения.
 превзойдет некоторое граничное значение, определяемое моментом касания кривой 1 с кривой 3 или 4. превзойдет некоторое граничное значение, определяемое моментом касания кривой 1 с кривой 3 или 4.
Аналогично определяются автоколебания и при наличии жесткой обратной связи, как показано на рис. 18.44, в.


Аналогично можно определить амплитуду первой гармоники автоколебаний для других переменных в данной системе.

б)
|