Теория систем автоматического управленияОценка качества нелинейных процессов управления
Приближенное исследование колебательных переходных процессов
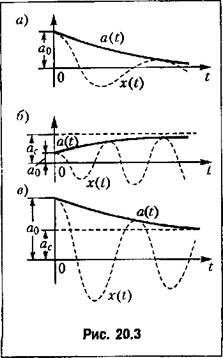
Рассмотрим симметричные относительно оси времени колебательные переходные процессы в нелинейной автоматической системе, которые в первом грубом приближении могут быть описаны затухающей или расходящейся синусоидой с медленно меняющимися во времени показателем затухания и частотой (рис. 20.1).
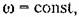 пишут пишут

 в процессе колебаний меняются с течением времени, то решение следует записывать в другом виде. в процессе колебаний меняются с течением времени, то решение следует записывать в другом виде.
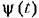 и определять текущее значение частоты в произвольный момент времени в виде и определять текущее значение частоты в произвольный момент времени в виде

причем

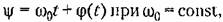 причем согласно (20.2) текущее значение частоты причем согласно (20.2) текущее значение частоты
Однако в данной задаче целесообразно придерживаться первого представления ((20.2) и (20.3)).
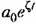 , как сделано в (20.1), а в виде дифференциальной , как сделано в (20.1), а в виде дифференциальной
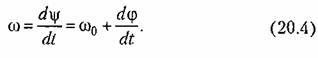

Зависимости

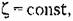 получаем как частный случай получаем как частный случай

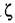 меняется в процессе колебаний, текущее значение амплитуды согласно (20.5) будет меняется в процессе колебаний, текущее значение амплитуды согласно (20.5) будет

т. е. огибающая колебаний (рис. 20.1) состоит из элементарных отрезков экспонент с
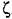 . .
Итак, будем искать решение для переходного процесса в нелинейной системе как первое приближение в виде


Показатель затухания может характеризовать быстроту не только затухания, но и расхождения колебаний:

т. е. положительным значениям показателя затухания ^ соответствуют расходящиеся колебания.
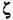 могут характеризовать как те, так и другие процессы. могут характеризовать как те, так и другие процессы.
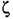 не мала, то, дифференцируя выражение (20.7) по времени как произведение двух функций, с учетом (20.8) находим не мала, то, дифференцируя выражение (20.7) по времени как произведение двух функций, с учетом (20.8) находим
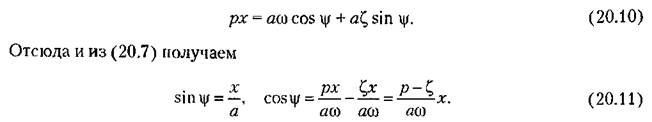
 вместо (18.6) здесь будет вместо (18.6) здесь будет
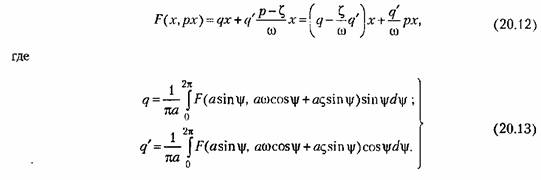
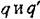 сохраняют прежний вид: сохраняют прежний вид:
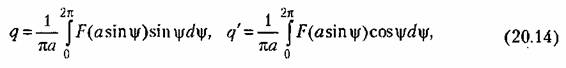
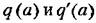 для различных конкретных нелинейностей, учитывая, однако, новую форму (20.12) замены нелинейной функции. для различных конкретных нелинейностей, учитывая, однако, новую форму (20.12) замены нелинейной функции.
В случае нелинейных систем первого класса дифференциальное уравнение колебательного переходного процесса
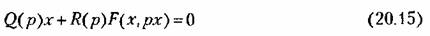
при наличии свойства фильтра (§ 18.2) после гармонической линеаризации согласно (20.12) принимает вид
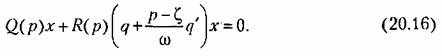
 характеристического учвнения гармонически линеаризованной системы (20.16). характеристического учвнения гармонически линеаризованной системы (20.16).
В соответствии с этим в характеристическое уравнение

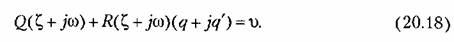
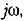 например: например:

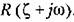
 , ограничиваясь его первой степенью, а именно: , ограничиваясь его первой степенью, а именно:
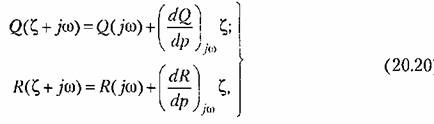 ) )
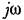 вместо? в выражения для производных. вместо? в выражения для производных.
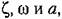 причем причем
 . Поэтому указанное комплексное уравнение позволяет найти . Поэтому указанное комплексное уравнение позволяет найти
две переменные как функцию третьей:

 и частоты со с изменением амплитуды а затухающего или расходящегося колебательного процесса в нелинейной системе. и частоты со с изменением амплитуды а затухающего или расходящегося колебательного процесса в нелинейной системе.
 для первого приближения для первого приближения
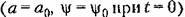 следующие выражения: следующие выражения:

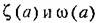 — найденные ранее функции (20.21). — найденные ранее функции (20.21).
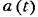 из первого. из первого.
В результате получаем решение


 а также характером их изменения в зависимости от амплитуды колебаний и от параметров системы. а также характером их изменения в зависимости от амплитуды колебаний и от параметров системы.
 означает какой-либо из основных подлежащих выбору параметров системы (коэффициент усиления или др.). означает какой-либо из основных подлежащих выбору параметров системы (коэффициент усиления или др.).
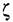 и частоты со нелинейных колебательных переходных процессов с изменением величины амплитуды колебаний а. и частоты со нелинейных колебательных переходных процессов с изменением величины амплитуды колебаний а.
 соответствует отсутствию затухания, т. е. сохранению с течением соответствует отсутствию затухания, т. е. сохранению с течением
Первые соответствуют расходящимся колебаниям, а вторые — затухающим.
 (где задана начальная амплитуда (где задана начальная амплитуда
 вниз. Процесс изменения амплитуды во времени показан на рис. 20.3, а. Изменение частоты со (а) определяется при этом по соответствующей вертикали на нижней части рис. 20.2. вниз. Процесс изменения амплитуды во времени показан на рис. 20.3, а. Изменение частоты со (а) определяется при этом по соответствующей вертикали на нижней части рис. 20.2.

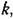 лежащая правее точки Д является областью существования автоколебаний, к которой сходятся колебательные переходные процессы с обеих сторон (снизу и сверху). При этом положение равновесия системы (любая точка а = 0 па оси абсцисс) в данной области значений параметр к является неустойчивым, так как колебания в переходном процессе от него расходятся, стремясь к другому устойчивому состоянию — автоколебательному режиму. лежащая правее точки Д является областью существования автоколебаний, к которой сходятся колебательные переходные процессы с обеих сторон (снизу и сверху). При этом положение равновесия системы (любая точка а = 0 па оси абсцисс) в данной области значений параметр к является неустойчивым, так как колебания в переходном процессе от него расходятся, стремясь к другому устойчивому состоянию — автоколебательному режиму.
Левее же точки В (рис. 20.2) лежат знамения параметра а, при которых переходный процесс затухает от любой начальной амплитуды а0до пуля. Это есть область устойчивости равновесного состояния системы.
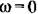 (рис. 20.2) лежит обычно область монотонных переходных процессов. (рис. 20.2) лежит обычно область монотонных переходных процессов.
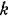 и др.), то они могут служить хорошим материалом для выбора наилучших параметров нелинейной системы при ее проектировании или синтезе. и др.), то они могут служить хорошим материалом для выбора наилучших параметров нелинейной системы при ее проектировании или синтезе.
Обратимся теперь к способам построения этих диаграмм.
Первый способ. Выделив в уравнении (20.18) вещественную Х и мнимую Участи, подобно тому как это делалось в главе 18, получим два уравнения:

Пусть требуется построить диаграмму качества затухания нелинейных колебаний по некоторому параметру системы к, который входит в коэффициенты уравнений (20.24). Выразив на основании одного из этих уравнений величину

и подставив ее в другое из уравнений (20.24), найдем
 I I
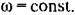
Второй способ. Характеристическое уравнение (20.17) можно записать в
развернутом виде:

 (в простейших задачах только от а). Разложим левую часть уравнения (в простейших задачах только от а). Разложим левую часть уравнения
(20.27) на два сомножителя:

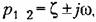 определяющей колебательный переходный процесс в исследуемой системе. Тогда получаем определяющей колебательный переходный процесс в исследуемой системе. Тогда получаем
 ) )
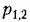 при принятых начальных условиях, было основным. Коэффициенты разложения (20.28) связаны следующими соотношениями; при принятых начальных условиях, было основным. Коэффициенты разложения (20.28) связаны следующими соотношениями;
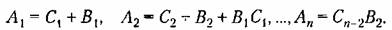
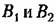 через коэффициенты первоначального уравнения (20.27). через коэффициенты первоначального уравнения (20.27).
В частности, для характеристического уравнения, третьей степени
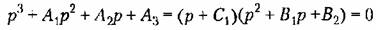
имеем:
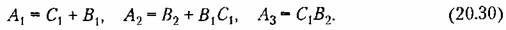
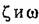 (20.29) определяли основную часть решения, а третий корень уравнения можно было не учитывать, нужно, чтобы (20.29) определяли основную часть решения, а третий корень уравнения можно было не учитывать, нужно, чтобы

 , которые следует брать при построении диаграммы качества. , которые следует брать при построении диаграммы качества.
 Составим предпоследний определитель Гурвица: Составим предпоследний определитель Гурвица:
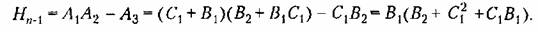
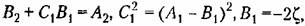 то полученное выше выражение можно записать в виде то полученное выше выражение можно записать в виде
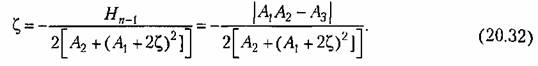
Далее, поскольку из (20.30) следует, что
4

то из (20.29) получаем формулу для квадрата частоты:

Формулы (20.22) и (20.23) позволяют строить диаграммы качества для систем третьего порядка.
Аналогично для системы четвертого порядка получаем

Здесь требуется, соблюдение того же условия (20.31).
Исходя из выражения предпоследнего определителя Гурвица, аналогичным путем находим формулу
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
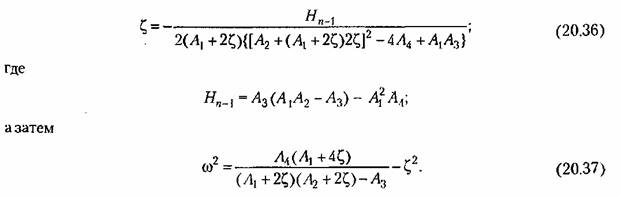

 выражение (20.18) можно представить в виде выражение (20.18) можно представить в виде
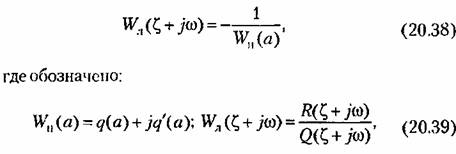
 ). Этим самым определяется ). Этим самым определяется
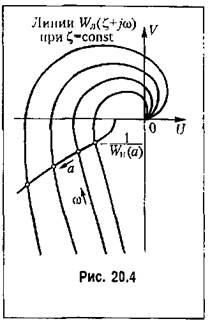
качество колебательного переходного процесса при всех заданных параметрах системы, т. е. определяются точки одной вертикали на диаграмме качества (рис. 20.2). Повторив такие же построения (рис. 20.4) для различных значений выбираемого параметра системы к, можно построить и всю диаграмму качества (рис. 20.2).
Способы построения диаграмм качества для систем второго класса и другие применения диаграмм см. в [72]. Там же рассматриваются несимметричные колебательные процессы и скользящие процессы.
|