Теория систем автоматического управленияПримеры исследования колебательных переходных процессов
Рассмотрим сначала построение диаграммы качества и кривой переходного процесса на примере нелинейной следящей системы, а затем исследуем переходный процесс в нелинейной системе с логическим устройством.
Пример 1 . Структурная схема следящей системы изображена па рис. 20.5, где 1 — датчик рассогласования, 2 — усилитель, 3 — реле, 4 — исполнительный двигатель, 5 — редуктор, 6 — управляемый объект, 7 — дополнительная обратная связь.
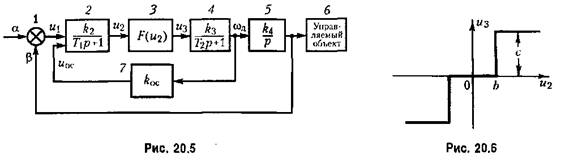
Системы с такой структурной схемой находят применение в тех случаях, когда для управления двигателем нужна значительная мощность, а увеличение габаритов и массы усилителя нежелательно.
Для датчика рассогласования системы имеем уравнения

 — соответственно входная и выходная величины системы; кх — коэффициент — соответственно входная и выходная величины системы; кх — коэффициент
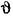 — рассогласование. — рассогласование.
Статическая характеристика нелинейного звена — реле — изображена на рис. 20.6. Выполняя гармоническую линеаризацию нелинейной характеристики реле, получим уравнение

где в соответствии с (18.16) для однозначной релейной характеристики с зоной нечувствительности коэффициент гармонической линеаризации определяется формулой

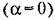 следящей системы в виде следящей системы в виде

Характеристическое уравнение, соответствующее полученному, дифференциальному уравнению, будет

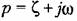 с использованием формулы (20.19). с использованием формулы (20.19).
 которое в результате распадается на которое в результате распадается на
следующие два уравнения:

Из последнего уравнения определяем квадрат частоты:

 в уравнение (20.45), получим в уравнение (20.45), получим

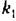 . В результате получим . В результате получим

 с =120 В. с =120 В.
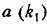
 . Эти кривые представляют собой диаграмму . Эти кривые представляют собой диаграмму
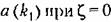 соответствует автоколебаниям. соответствует автоколебаниям.
Выполним теперь построение диаграммы качества но второму способу, указанному в §20.1.
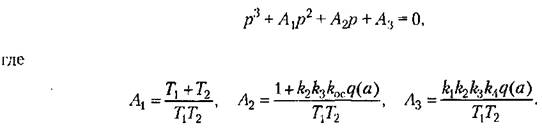
Уравнение (20.44) запишем в виде
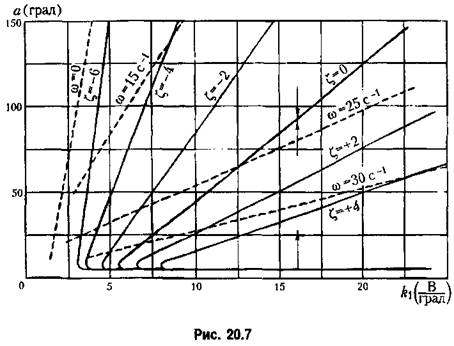
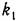 при выбранных значениях других параметров следящей системы это дает тот же результат, что и в предыдущем случае. при выбранных значениях других параметров следящей системы это дает тот же результат, что и в предыдущем случае.
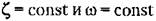 накладываются друг на друга. накладываются друг на друга.

Сравнивая полученные диаграммы для случаев наличия дополнительной обратной связи и отсутствия обратной связи, убеждаемся, что за счет
раметры последней, а также дают возможность решить и обратную задачу, т. е. выбрать значения параметров из условия заданного качества переходного процесса. Кроме того, по диаграммам качества легко построить огибающую амплитуд переходного процесса и найти изменение частоты процесса от периода к периоду, т. е. в конечном счете выполнить приближенное построение переходного процесса.
 В. На том же рис. 20.9 изображена пунктиром В. На том же рис. 20.9 изображена пунктиром
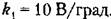 . В данном случае в . В данном случае в
установившемся режиме имеют место автоколебания с амплитудой а = 42 В.

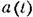 , найденная но методу гармонической линеаризации на основании диаграммы качества. , найденная но методу гармонической линеаризации на основании диаграммы качества.
Приближенный метод дает достаточно хорошие результаты и в том случае, когда колебания затухают практически за один период (рис. 20.12).
 которые изучались в§ 18.4. которые изучались в§ 18.4.
 и частоты со. и частоты со.
Формула для гармонической линеаризации, нелинейности вместо (18.153) принимает вид
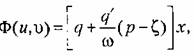
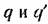 определяются прежними формулами определяются прежними формулами
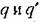 тригонометрических тригонометрических
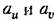 через а через а
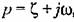 , что дает , что дает

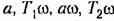 |) должны быть поставлены соответственно выражения: |) должны быть поставлены соответственно выражения:
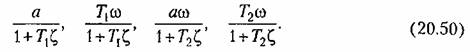

Характеристическое уравнение вместо (18.155) примет вид

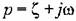 по формуле (20.19) получаем вещественную и мнимую части: по формуле (20.19) получаем вещественную и мнимую части:

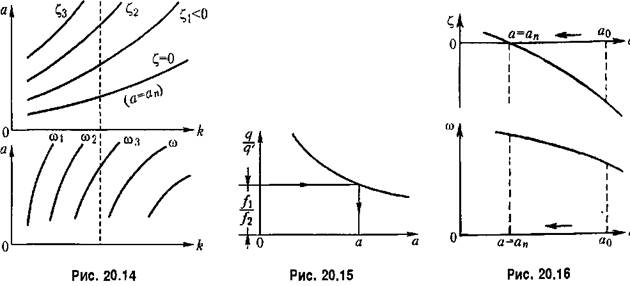
Отсюда находим:
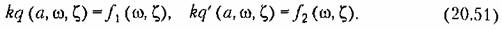
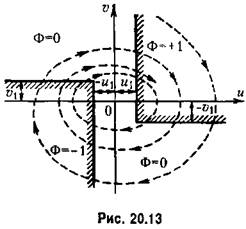
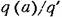 (рис. 20.15). (рис. 20.15).
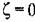 I соответствует зависимости амплитуды установившихся автоколебаний от коэффициента усиления к. I соответствует зависимости амплитуды установившихся автоколебаний от коэффициента усиления к.
 . (рис. 20.14, пунктир). . (рис. 20.14, пунктир).
Результат показан на рис. 20,16. Это позволяет судить о быстроте затухания и о количестве колебаний за время переходного процесса.
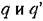 (18.151) с подстановками (18.151) и (18.152). Кроме того, в написанных выше выражениях для X и У нужно сохранить только первую степень (18.151) с подстановками (18.151) и (18.152). Кроме того, в написанных выше выражениях для X и У нужно сохранить только первую степень

В принципе решение не меняется. Изложенный метод решения задачи отличается тем, что он одинаково пригоден к различным системам, описываемым уравнениями любого порядка, и не связан с построением годографов па комплексной плоскости.
Более подробно применение логических устройств, нелинейных алгоритмов управления и нелинейных корректирующих средств рассмотрено в работах [74,75,94 ] и др.
|