Теория систем автоматического управления
Несимметричные вынужденные колебания с медленно меняющейся составляющей
Вынужденные колебания будут несимметричными в следующих случаях:
при несимметричных нелинейных характеристиках системы;
при наличии постоянного или медленно меняющегося внешнего воздействия (в статических системах);
при наличии постоянной или медленно меняющейся скорости изменения внешнего воздействия (в астатических системах).
В общем случае будем полагать, что к нелинейной системе приложены два внешних воздействия, вследствие чего ее уравнение вместо (21.2) имеет вид
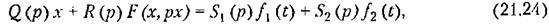
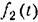 — периодическое внешнее воздействие: — периодическое внешнее воздействие:
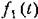
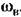
Решение уравнения (21.24) будем искать в виде

 может производиться может производиться
но формуле, аналогичной (19.5):
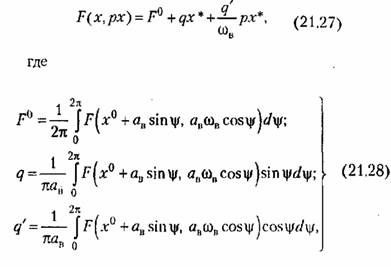
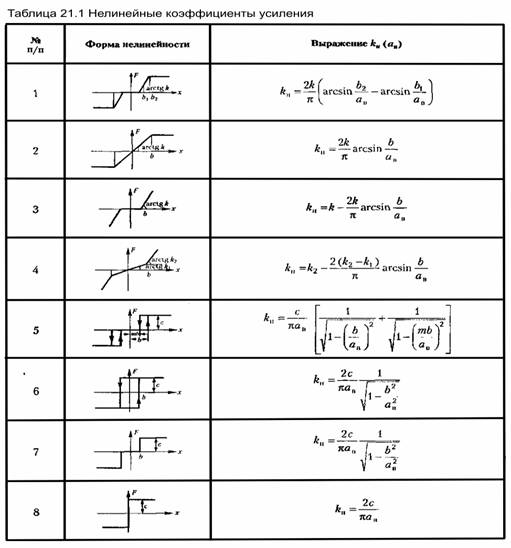
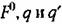 , приведенными в главе 19. Таким образом, для каждой конкретной нелинейности имеются готовые выражения: , приведенными в главе 19. Таким образом, для каждой конкретной нелинейности имеются готовые выражения:
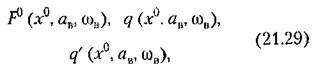
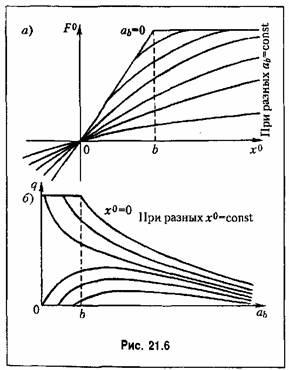
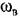 в них отсутствует. В качестве примера на рис. 21.6 приведены эти зависимости для нелинейности типа насыщения, аналогичные приведенным в главе 19. в них отсутствует. В качестве примера на рис. 21.6 приведены эти зависимости для нелинейности типа насыщения, аналогичные приведенным в главе 19.
По аналогии с формулой (21.4) запишем

 в заданное дифференциальное уравнение нелинейной системы (21.24), получим уравнение в заданное дифференциальное уравнение нелинейной системы (21.24), получим уравнение
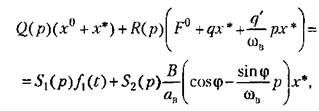
которое разбивается нелинейным образом (см. главу 19) на два уравнения соответственно для медленно меняющихся и для колебательных составляющих:
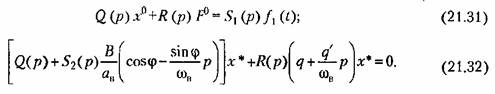

 привести уравнение (21.32) к следующему: привести уравнение (21.32) к следующему:
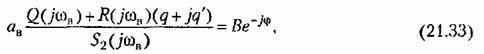
в результате решения которого любым из двух методов (графическим или аналитическим), описанных в § 21.1, определяются зависимости амплитуды а^ и сдвига фазы фот величины смещениях0, т. е.
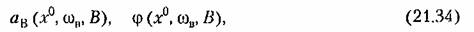
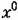 остается пока еще неизвестным. остается пока еще неизвестным.
 Уравнение аналитического метода (21.17) примет вид Уравнение аналитического метода (21.17) примет вид
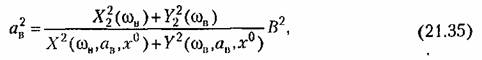
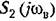 и выражения и выражения
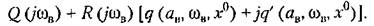
Уравнение (21.35) не решается так просто, как (21.17). Однако можно применить следующий графический прием его решения. Разбив (21.35) на два уравнения:
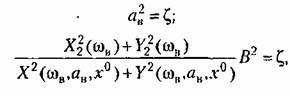
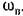
Подставив теперь значение амплитуды ап в первое из выражений (21.29), найдем функцию смещения в виде которая является характеристикой данного нелинейного звена системы по отношению к медленно меняющимся составляющим переменных Fи x . Эти медленно меняющиеся составляющие определяются затем путем решения дифференциального уравнения (21.31), в которое надо подставить найденную функцию смещения (21.36).
 от характера изменения и места приложения медленно меняющихся внешних воздействий здесь остается в силе, как было и при автоколебаниях. от характера изменения и места приложения медленно меняющихся внешних воздействий здесь остается в силе, как было и при автоколебаниях.
Однако принципиальным отличием функции смешения (21.36), определяющей прохождение медленно меняющихся сигналов через нелинейную систему при наличии вынужденных колебаний, от функции смещения (19.13) при автоколебаниях
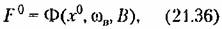 существенная завнеимость ее от частоты и амплитуды внешнего периодического воздействия (в то время как при автоколебаниях вид функции смещения зависел только от структуры и от соотношения параметров самой системы). существенная завнеимость ее от частоты и амплитуды внешнего периодического воздействия (в то время как при автоколебаниях вид функции смещения зависел только от структуры и от соотношения параметров самой системы).
 , зависящее только от структуры и параметров самой системы, входящих в уравнение (21.33). , зависящее только от структуры и параметров самой системы, входящих в уравнение (21.33).
Здесь, так же как и в главе 19, возможен и второй метод отыскания функции смешения. При этом методе попутно определяются также статические и установившиеся ошибки. Метод состоит в следующем.
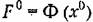 не зависит от характера изменения и места приложения медленно меняющихся воздействий, то ее можно определить для не зависит от характера изменения и места приложения медленно меняющихся воздействий, то ее можно определить для
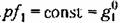 ). ).
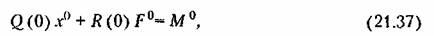 вид вид
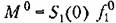 или для астатических систем или для астатических систем
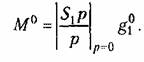
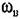 ) )

из уравнения (21.37) находим

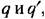 определяемые второй и третьей из формул (21.29), получим зависимости определяемые второй и третьей из формул (21.29), получим зависимости
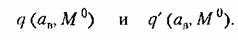
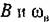 находим амплитуду вынужденных находим амплитуду вынужденных
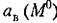 в (21.38) и (21.39), получаем зависимости в (21.38) и (21.39), получаем зависимости
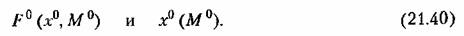
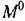 от величины постоянного внешнего воздействия. Это яркий пример неприменимости принципа суперпозиции для нелинейных систем и в то же время иллюстрация достоинства развиваемого здесь метода, который позволяет это уловить, несмотря на приближенность решения задачи. от величины постоянного внешнего воздействия. Это яркий пример неприменимости принципа суперпозиции для нелинейных систем и в то же время иллюстрация достоинства развиваемого здесь метода, который позволяет это уловить, несмотря на приближенность решения задачи.
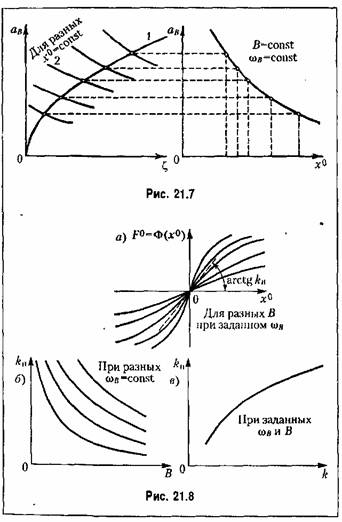
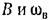 (рис. 21.8, а), (рис. 21.8, а),
Итак, наличие в нелинейной системе вынужденных колебаний с частотой внешнего периодического воздействия приводит к эффекту вибрационного сглаживания нелинейности, как и при автоколебаниях. При этом согласно (21.31) для медленно протекающих процессов в условиях вынужденных вибраций исходное дифференциальное уравнение системы (21.24) заменяется уравнением
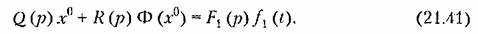
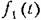 является медленно меняющимся. является медленно меняющимся.
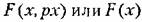 может быть скачкообразной (релейной), петлевой, с может быть скачкообразной (релейной), петлевой, с
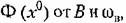 что будет подробнее рассмотрено ниже. что будет подробнее рассмотрено ниже.
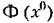 (рис. 21.8, а) позволяет произвести обычную линеаризацию, а именно на некотором участке вблизи начала координат можно принять (рис. 21.8, а) позволяет произвести обычную линеаризацию, а именно на некотором участке вблизи начала координат можно принять

где

Тогда все медленно протекающие процессы в данной нелинейной системе можно будет рассчитывать не по уравнению (21.41), а по линейному уравнению
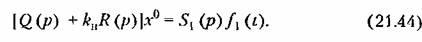
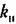 (рис. 21.8, а) будет -зависеть не только от структуры и параметров самой системы, как было при автоколебаниях, но также и от амплитуды В и частоты сов внешнего периодического воздействия, которые могут меняться в известных пределах независимо от самой системы. Поэтому вибрационное сглаживание нелинейных характеристик при помощи вынужденных колебаний обладает значительно большими практическими возможностями, чем при автоколебаниях, и довольно часто применяется в технике, особенно в релейных системах автоматического управления. Однако в некоторых случаях вибрационное сглаживание может приводить к вредным последствиям, вплоть до потери устойчивости системы. (рис. 21.8, а) будет -зависеть не только от структуры и параметров самой системы, как было при автоколебаниях, но также и от амплитуды В и частоты сов внешнего периодического воздействия, которые могут меняться в известных пределах независимо от самой системы. Поэтому вибрационное сглаживание нелинейных характеристик при помощи вынужденных колебаний обладает значительно большими практическими возможностями, чем при автоколебаниях, и довольно часто применяется в технике, особенно в релейных системах автоматического управления. Однако в некоторых случаях вибрационное сглаживание может приводить к вредным последствиям, вплоть до потери устойчивости системы.
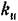 при линеаризации функции смещения можно производить, как было показано в § 19.2, не по формуле (21.43), а по более простой формуле: при линеаризации функции смещения можно производить, как было показано в § 19.2, не по формуле (21.43), а по более простой формуле:

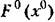 рис. 21.6, а рис. 21.6, а
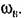
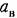 (рис. 21.2, в), фигурирующая па рис. 21.6, в. (рис. 21.2, в), фигурирующая па рис. 21.6, в.
|