Теория систем автоматического управленияЗависимость устойчивости и качества нелинейных систем от внешних вибраций
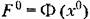 открывается возможность исследовать по уравнению (21.41) или по линейному уравнению (21.44) любые медленно меняющиеся процессы в системе. открывается возможность исследовать по уравнению (21.41) или по линейному уравнению (21.44) любые медленно меняющиеся процессы в системе.
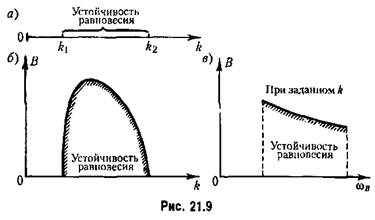
Устойчивость системы по медленно меняющейся составляющей можно рассматривать тоже путем исследования нелинейного уравнения (21.41) или же линейного уравнения (21.44).
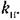 Это является совершенно новым и очень важным специфически нелинейным фактором, который в предыдущих главах еще не встречался. В линейных системах такое явление вообще отсутствует. Это является совершенно новым и очень важным специфически нелинейным фактором, который в предыдущих главах еще не встречался. В линейных системах такое явление вообще отсутствует.
При использовании линейного уравнения (21.44) можно применять обычные критерии устойчивости линейных систем (Гурвина, Найквиста) и обычные логарифмические частотные характеристики.
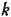 зависимость критической амплитуды внешних вибраций от частоты (рис. 21.9, в) — границу вибрационной помехоустойчивости системы. зависимость критической амплитуды внешних вибраций от частоты (рис. 21.9, в) — границу вибрационной помехоустойчивости системы.
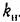 . Зависимость же величины кп от любого параметра системы нетрудно найти предварительно согласно § 21.2 (см., например, рис. 21.8,1?). . Зависимость же величины кп от любого параметра системы нетрудно найти предварительно согласно § 21.2 (см., например, рис. 21.8,1?).
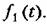
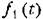 изменяется периодически, т. е. имеется возможность исследования двухчастотиых вынужденных колебаний нелинейной системы при большой разнице частот. Можно и здесь (как в изменяется периодически, т. е. имеется возможность исследования двухчастотиых вынужденных колебаний нелинейной системы при большой разнице частот. Можно и здесь (как в
§ 19.2) проводить разделение общего движения нелинейной системы не только на два, но и на три вида по степени медленности движения во времени.
 внешнего периодического воздействия (вибраций), что в некоторых случаях на практике может оказаться решающим для создания качественной автоматической системы. внешнего периодического воздействия (вибраций), что в некоторых случаях на практике может оказаться решающим для создания качественной автоматической системы.
Изложенная общая теория поведения нелинейных автоматических систем при наличии внешнего периодического воздействия (вибраций) может значительно упрощаться в различных частных задачах.
Приведем здесь видоизменение этой общей теории для следующих двух наиболее типичных частных задач:
приложение специального внешнего периодического воздействия с целью вибрационного сглаживания нелинейности (с последующей линеаризацией сглаженной характеристики при расчете системы в целом);
исследование работы нелинейной автоматической системы при высокочастотных внешних вибрационных помехах, когда не все звенья системы пропускают эти вибрации.
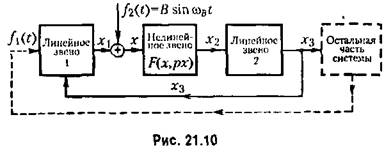
 (рис. 21.10) специально для того, чтобы произвести (рис. 21.10) специально для того, чтобы произвести
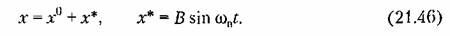

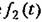 предполагается приложен- предполагается приложен-
ным к системе непосредственно там же, где их (рис. 21.10), то в уравнении (21.24), составленном для исследуемой части системы (не включая пунктирной части па рис. 21.10), будет

На основании (21.47) по первой из формул (21.28) находим
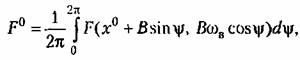
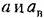 па величину В. Как видим, здесь совершенно отпадает па величину В. Как видим, здесь совершенно отпадает
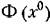
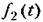 медленно меняющимся. медленно меняющимся.
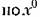 совпадаете полной производной. совпадаете полной производной.
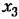 . С этой целью подставим равенства (21.47) и (21.48) в уравнение (21.33). Тогда для удовлетворения последнего уравнения необходимо потребовать, чтобы модуль отношения . С этой целью подставим равенства (21.47) и (21.48) в уравнение (21.33). Тогда для удовлетворения последнего уравнения необходимо потребовать, чтобы модуль отношения
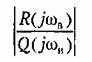
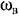 должна лежать за пределами полосы пропускания всей линейной части рассматриваемого участка системы (блоки 1 и 2). должна лежать за пределами полосы пропускания всей линейной части рассматриваемого участка системы (блоки 1 и 2).
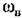 также и за пределами полосы пропускания отдельного блока 2 исследуемой системы (рис. 21.10). также и за пределами полосы пропускания отдельного блока 2 исследуемой системы (рис. 21.10).
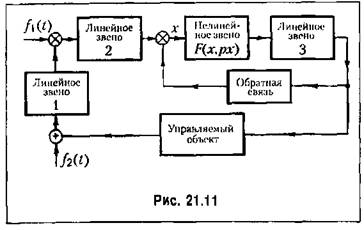
Задача 2 . Пусть на какую-нибудь систему автоматического управления (рис. 21.11) воздействует внешняя вибрационная помеха
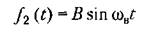
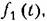 которое по отношению к помехе является медленно меняющимся. Уравнение динамики системы приводится к виду (21.24). которое по отношению к помехе является медленно меняющимся. Уравнение динамики системы приводится к виду (21.24).
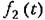 Однако в Однако в
данной задаче этот общий метод решения можно упростить. Рассмотрим два случая. В том случае, когда вся приведенная линейная часть системы (риг. 21.11), определяемая передаточной функцией

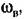 уравиение (21.33)"можно записать виде уравиение (21.33)"можно записать виде
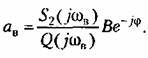
Тогда амплитуда вибраций на входе нелинейного звена будет определяться формулой
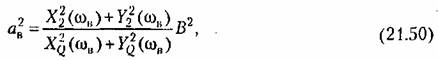
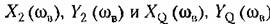 > обо- > обо-
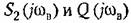
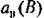 с разными коэффициентами пропорциональности для разных частот вибраций 0)в (рис, 21.12). В частности, для схемы рис. 21.11 они будут определяться структурой линейных блоков 1 и 2. с разными коэффициентами пропорциональности для разных частот вибраций 0)в (рис, 21.12). В частности, для схемы рис. 21.11 они будут определяться структурой линейных блоков 1 и 2.
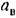 на входе нелинейного звена в этом случае не зависит от на входе нелинейного звена в этом случае не зависит от
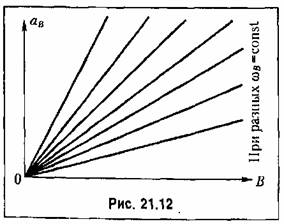
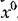 . Поэтому здесь, как . Поэтому здесь, как
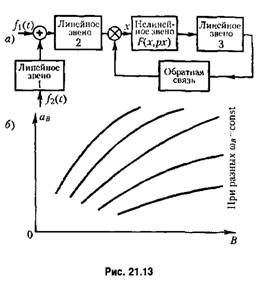
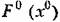 будет будет
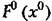 и ее крутизна и ее крутизна
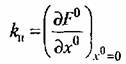
будут зависеть не только от амплитуды В, но и от частоты сов вибрационных помех, а также, конечно, и от параметров линейных блоков 1 и 2 (рис. 21.11), входящих в формулу (21.50).
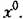 Однако и в этом случае возможно упрощение решения задачи по сравнению с общей теорией, состоящее в том, что при определении функции смещения выбрасывается часть системы, не пропускающая вибраций (рис. 21.13, а). Однако и в этом случае возможно упрощение решения задачи по сравнению с общей теорией, состоящее в том, что при определении функции смещения выбрасывается часть системы, не пропускающая вибраций (рис. 21.13, а).
В этом случае нужно записать уравнение динамики только оставшейся части системы (рис. 21.13, а):
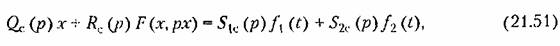
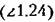 . Отсюда но аналогии с (21.35) . Отсюда но аналогии с (21.35)
получим уравнение для определения амплитуды вибраций на входе нелинейного звена в виде
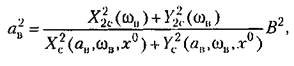
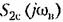 и для выражения и для выражения
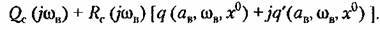
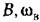 ) графическим приемом, описанным в §21.2 (рис. 21.7). ) графическим приемом, описанным в §21.2 (рис. 21.7).
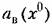 подставляется затем в первую из формул (21.29) подставляется затем в первую из формул (21.29)
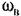 внешних вибраций и от параметров системы, входящих в выделенную часть контура (рис. 21.13, а). внешних вибраций и от параметров системы, входящих в выделенную часть контура (рис. 21.13, а).
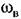 вибрационных помех. вибрационных помех.
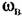 ), что система может выйти из строя но этой причине раньше, чем перестанет различаться полезный сигнал иа уровне помех. Это очень важно учитывать на практике. ), что система может выйти из строя но этой причине раньше, чем перестанет различаться полезный сигнал иа уровне помех. Это очень важно учитывать на практике.
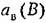 будет при этом, в отличие от первого случая, криволинейной (рис. 21.13, б). будет при этом, в отличие от первого случая, криволинейной (рис. 21.13, б).
В заключение заметим, что тем же методом, что и в § 18.5, легко вычислять высшие гармоники вынужденных колебаний (см. § 9.4 книги [72]).
|