Теория систем автоматического управленияСлучайные процессы в нелинейных системах
Статистическая линеаризация нелинейностей
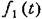 в (21.44) являются медленно меняющимися случайными процессами с нормальным законом распределения (см. подробнее § 10.1 в книге [72]). в (21.44) являются медленно меняющимися случайными процессами с нормальным законом распределения (см. подробнее § 10.1 в книге [72]).
Для решения других задач при случайных воздействиях удобно бывает применять так называемую статистическую линеаризацию нелинейностей, разработанную П. Е. Казаковым [38]. Сущность ее заключается в следующем.
Для оценки динамической точности автоматических систем при случайных воздействиях будем определять два первых вероятностных момента случайных процессов: математическое ожидание (среднее значение) и дисперсию (или среднеквадратичное отклонение). Последнее эквивалентно определению спектральной плотности или корреляционной функции.
Если нелинейная система описывается дифференциальным уравнением
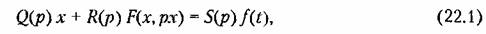

 в нелинейном звене Р (х, рх) существенно связано с высшими вероятностными моментами (подобно тому как в главе 18 приходилось иметь дело с высшими гармониками). Ввиду замкнутости контура системы это обстоятельство накладывает отпечаток и на все процессы в данной системе. Поэтому точное решение задачи в большинстве случаев оказывается недоступным. в нелинейном звене Р (х, рх) существенно связано с высшими вероятностными моментами (подобно тому как в главе 18 приходилось иметь дело с высшими гармониками). Ввиду замкнутости контура системы это обстоятельство накладывает отпечаток и на все процессы в данной системе. Поэтому точное решение задачи в большинстве случаев оказывается недоступным.
Достаточно хорошее для целей инженерных расчетов первое приближение применительно к рассматриваемым классам систем, обладающих свойством фильтра, дает пренебрежение высшими моментами, т. е. замена нелинейного звена эквивалентным линейным, которое одинаково с данным нелинейным преобразует два первых вероятностных момента: математическое ожидание (среднее значение) и дисперсию (или среднеквадратичное отклонение). Это и называется статистической линеаризацией нелинейности.
Эта операция по общей идее (но не по конкретному содержанию) аналогична тому как в главе 19 нелинейное звено при помощи гармонической линеаризации заменялось эквивалентным линейным, которое одинаково с данным нелинейным преобразует постоянную (или медленно меняющуюся) составляющую и первую гармонику колебательной составляющей, т. е. принимались во внимание два первых члена ряда Фурье и отбрасывались все высшие гармоники.
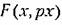 в виде в виде

 — случайная составляющая с нулевым математическим ожиданием (центрированная случайная функция времени). — случайная составляющая с нулевым математическим ожиданием (центрированная случайная функция времени).
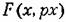 также представим в виде также представим в виде

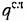 —эквивалентный коэффициент усиления случайной составляющей (центрированной). —эквивалентный коэффициент усиления случайной составляющей (центрированной).
Это выражение по форме тоже аналогично тому, которое применялось в главе 19, по имеет иное конкретное содержание.
Величина регулярной составляющей р определяется, следовательно, по известной формуле для математического ожидания. В случае однозначной нелинейной функции Р(х) эта формула дает

 — дифференциальный закон распределения случайной составляющей, например нормальный закон (рис. 11.10): — дифференциальный закон распределения случайной составляющей, например нормальный закон (рис. 11.10):

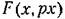 будет более сложное выражение: будет более сложное выражение:
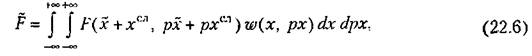
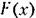 при симметричном законе распределения при симметричном законе распределения
(в том числе и нормальном) упрощается. Например, для нелинейности, показанной на рис. 22.2, будет
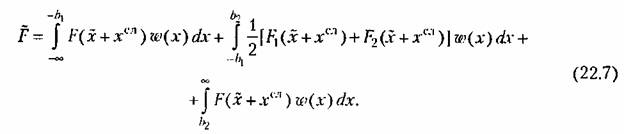
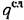 случайной составляющей в формуле (22.3) рекомендуется определять одним из следующих двух способов. случайной составляющей в формуле (22.3) рекомендуется определять одним из следующих двух способов.
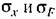 переменной .г и нелинейной функции F а именно: переменной .г и нелинейной функции F а именно:
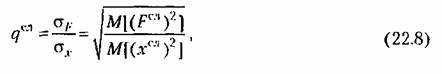
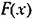 дает дает
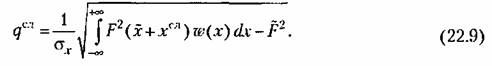

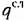 , обобщив (22.9) потому же образцу, как обобщены выражения (22,6) и (22.7) по сравнению с (22.4). , обобщив (22.9) потому же образцу, как обобщены выражения (22,6) и (22.7) по сравнению с (22.4).
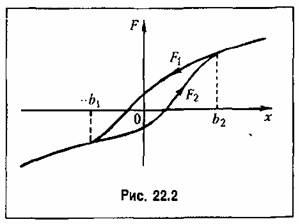
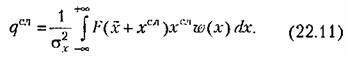
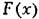
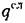 взять среднее арифметическое из двух; (22.8) н (22.10). взять среднее арифметическое из двух; (22.8) н (22.10).
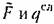 имели бы другие выражения). имели бы другие выражения).
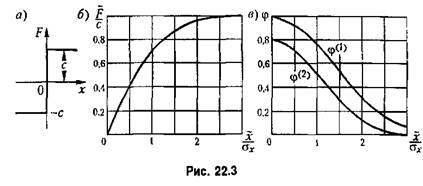
1. Идеальная релейная характеристика (рис, 22,3, а). Из формулы (22,4) находим
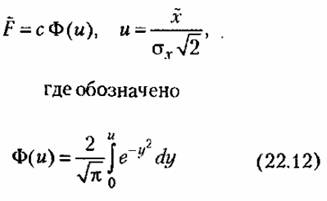
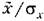 показана графически на рис. 22.3, б. показана графически на рис. 22.3, б.
По формулам (22.9) и (22.11) находим соответственно
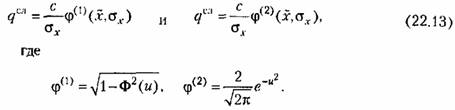
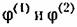 показаны на рис. 22.3, в. показаны на рис. 22.3, в.
2. Однозначная релейная характеристика с зоной нечувствительности (рис. 22.4, а). По формуле (22.4) с учетом обозначения (22.12) находим
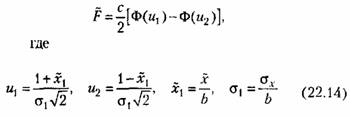
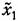 при при
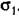
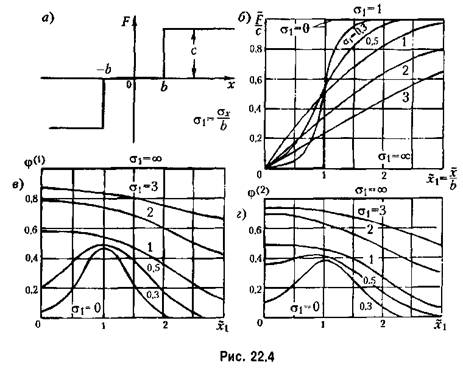
 По формулам (22.9) и (22.11) получаем выражения типа (22.13), где По формулам (22.9) и (22.11) получаем выражения типа (22.13), где
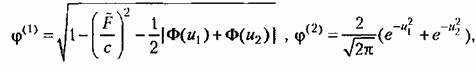
что изображено графически па рис. 22.4, в и г.
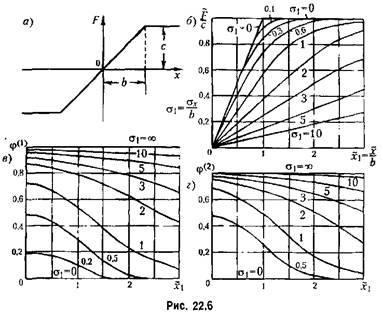
3. Петлевая релейная характеристика общего вида (рис. 22.5, а). По формулам (22.7) находим
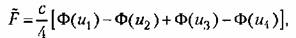
где кроме (22.14) и (22.12) введены еще обозначения

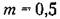 показана на рис. 22.5, б. показана на рис. 22.5, б.
Далее получаем выражения типа (22.13), где
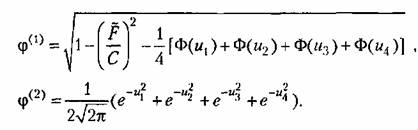
Эти функции для случая т = 0,5 изображены на рис. 22.5, в и г.
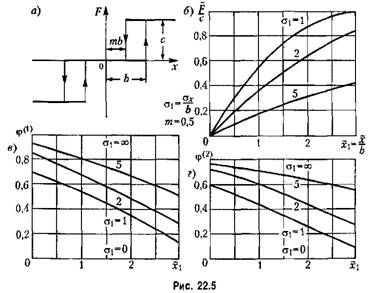
4. Характеристика типа насыщения (рис. 22.6, а). По формуле (22.4) с учетом
обозначений (22.12) и (22.14) находим
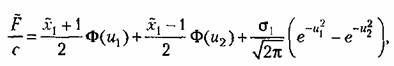
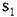 на рис. 22.6, б. По формулам же (22.9) и (22.11) находим выражение (22.13), где на рис. 22.6, б. По формулам же (22.9) и (22.11) находим выражение (22.13), где
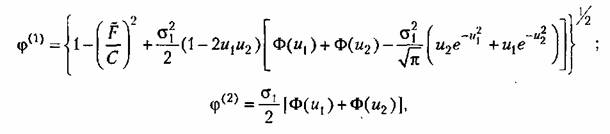
что изображено на рис. 22.6, в и г.
|