Теория систем автоматического управленияПозиционные звенья
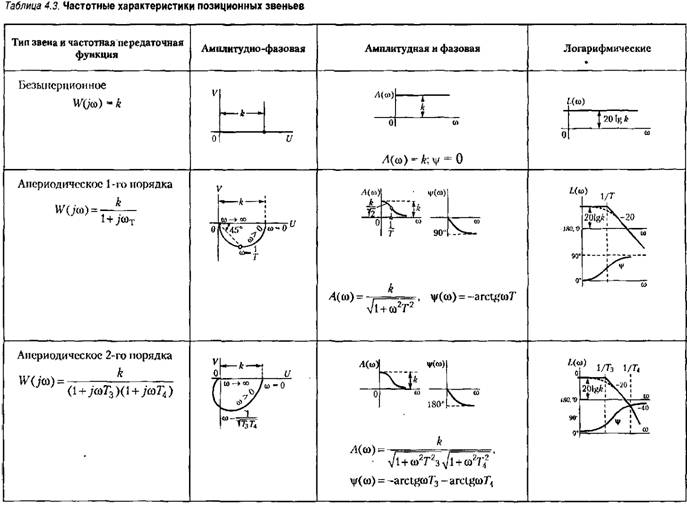
Характеристики позиционных звеньев сведены в табл. 4.2 и 4.3.
1. Безынерционное звено. Это звено не только в статике, но и в динамике опи сывается алгебраическим уравнением

Передаточная функция звена равна постоянной величине:

Примером такого звена являются механический редуктор (без учета явления скручивания и люфта), безынерционной (широкополосный) усилитель, делитель напряжения и т. п. Многие датчики сигналов, как, например, потенциометрические датчики, индукционные датчики, вращающиеся трансформаторы и т. п., также могут рассматриваться как безынерционные звенья.
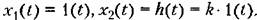 Функция веса представляет со- Функция веса представляет со-

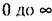 . Обычно к такому виду звена сводится одно из реальных звеньев, рассматриваемых ниже, например апериодическое или колебательное, если можно пренебречь влиянием динамических (переходных) процессов и этом звене, . Обычно к такому виду звена сводится одно из реальных звеньев, рассматриваемых ниже, например апериодическое или колебательное, если можно пренебречь влиянием динамических (переходных) процессов и этом звене,
2. Апериодическое звено первого порядка. Звено описывается дифференциальным уравнением
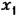 здесь является управляющее воздействие в двигателе, например подводимое напряжение в электрическом двигателе, расход жидкости в гидравлическом двигателе и т. и. Выходной величиной является скорость вращения ^. Дифференциальное уравнение движения при равенстве нулю момента нагрузки может быть представлено в виде здесь является управляющее воздействие в двигателе, например подводимое напряжение в электрическом двигателе, расход жидкости в гидравлическом двигателе и т. и. Выходной величиной является скорость вращения ^. Дифференциальное уравнение движения при равенстве нулю момента нагрузки может быть представлено в виде
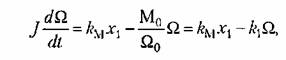
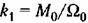 — наклон механической характеристики, равный отношению — наклон механической характеристики, равный отношению
пускового момента к скорости холостого хода при некотором значении управляющего воздействия.
Это уравнение приводится к виду
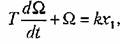
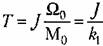 — постоянная времени — постоянная времени
двигателя. Оно полностью совпадаете (4.22).
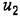

 -цени в соответствии со схемами, изображенными на рис. 4.10, д, также представляют собой апериодические звенья первого порядка. -цени в соответствии со схемами, изображенными на рис. 4.10, д, также представляют собой апериодические звенья первого порядка.
Во всех приведенных примерах дифференциальное уравнение движения совпадает с (4.22).
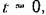

т. е. для положительного времени. Во многих случаях этот множитель опускается, но указанное обстоятельство необходимо иметь в виду.
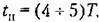
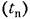 после подачи входного воздействия. после подачи входного воздействия.
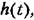 и она также приводится в табл. 4.2. и она также приводится в табл. 4.2.
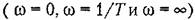
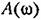 вдоль оси частот, или, как говорят, тем шире полоса пропускания частот у данного звена. вдоль оси частот, или, как говорят, тем шире полоса пропускания частот у данного звена.
Логарифмические частотные характеристики приведены в табл. 4.3. Л. а. х. строится по выражению
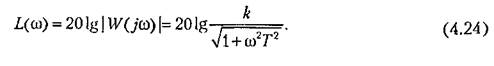
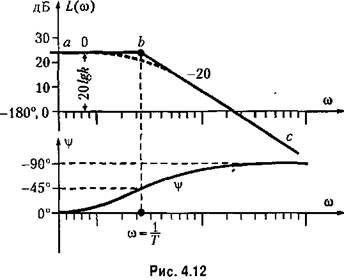
 , которому соответствует прямая линия, параллельная оси; частот (прямая аЬ) и являющаяся первой асимптотой. , которому соответствует прямая линия, параллельная оси; частот (прямая аЬ) и являющаяся первой асимптотой.
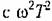 . Тогда вместо (4.24) будем иметь приближенное значение . Тогда вместо (4.24) будем иметь приближенное значение
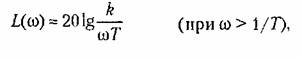
 ), являющаяся второй асимптотой. ), являющаяся второй асимптотой.
 и называется асимптотической л. а. х. Действительная л. а, х. (показана на рис. 4.12 пунктиром) будет несколько отличаться от асимптотической, причем наибольшее отклонение будет в точке Ь. Оно равно приблизительно 3 дБ, так как и называется асимптотической л. а. х. Действительная л. а, х. (показана на рис. 4.12 пунктиром) будет несколько отличаться от асимптотической, причем наибольшее отклонение будет в точке Ь. Оно равно приблизительно 3 дБ, так как
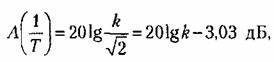
 на сопрягающей частоте (так как на сопрягающей частоте (так как
 и симметрия л. ф. х, относительно сопрягающей частоты. 3. Апериодическое звено второго порядка. Дифференциальное уравнение звена имеет вид и симметрия л. ф. х, относительно сопрягающей частоты. 3. Апериодическое звено второго порядка. Дифференциальное уравнение звена имеет вид

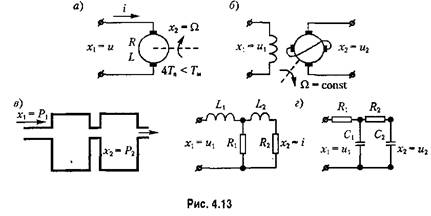
 В операторной записи уравнение (4.25) приобретает вид В операторной записи уравнение (4.25) приобретает вид
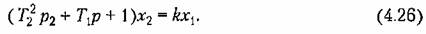
 часть последнего выражения разбивается на множители: часть последнего выражения разбивается на множители:
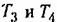
Примеры апериодических звеньев второго порядка приведены на рис. 4.13. Рассмотрим подробно случай двигателя постоянного тока (рис. 4.13, а). При отсутствии момента нагрузки на валу и при учете переходных процессов в цени якоря динамика Двигателя описывается двумя уравнениями, определяющими равновесие э. д. с. в цепи якоря:
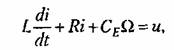
и равновесие моментов на валу двигателя:

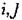 - приведенный момент инерции, А и К — индуктивность и сопротивление цепи якоря. - приведенный момент инерции, А и К — индуктивность и сопротивление цепи якоря.
Переходя в обоих уравнениях к операторной форме записи и решая их совместно, получим передаточную функцию двигателя постоянного тока при управлении напряжением якоря как отношение изображений скорости двигателя и напряжения якоря:
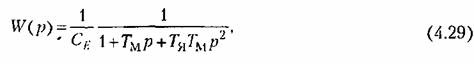
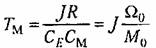 — электромеханическая постоянная времени двигателя, — электромеханическая постоянная времени двигателя,
 — скорость холостого хода и пусковой момент двигателя. — скорость холостого хода и пусковой момент двигателя.
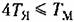
Переходная функция и функция веса звена приведены в табл. 4.2.
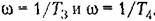

Л. а. х. строится по выражению
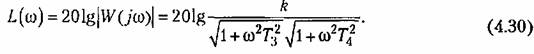

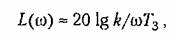 (4.30) заменяется приближенным (4.30) заменяется приближенным
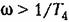 выражение (4.30) заменяется приближенным выражение (4.30) заменяется приближенным
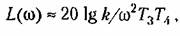
которому соответствует прямая с отрицательным наклоном -40 дБ/дек (третья асимптота). Действительная л. а. х. показана в табл. 4.3 пунктиром. Она отличается от асимптотической в точках излома на 3 дБ.
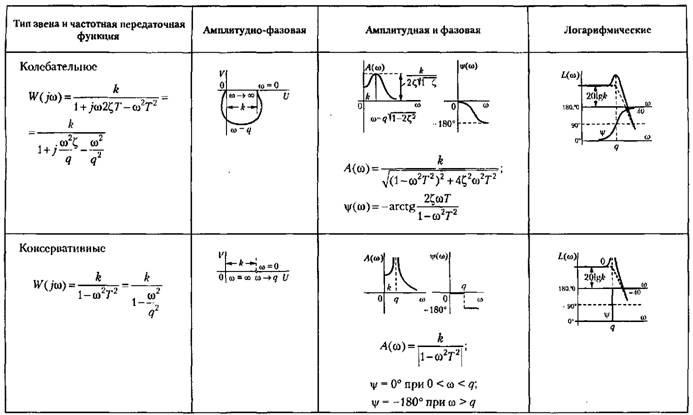
 должны быть комплексными, что будет должны быть комплексными, что будет
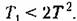
Левая

часть дифференциального уравнения обычно представляется в виде
 — угловая частота свободных колебаний (при отсутствии затухания), — угловая частота свободных колебаний (при отсутствии затухания),
 Передаточная функция колебательного звена Передаточная функция колебательного звена
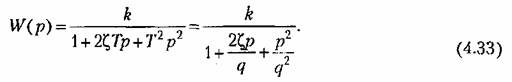
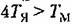 (рис. 4.14, 6), упругие механические передачи, например для передачи вращательного движения (рис. 4.14, в), с упругостью С, моментом инерции ] и коэффициентом скоростного трения 5, гироскопические элементы (рис. 4.14, г) и др. (рис. 4.14, 6), упругие механические передачи, например для передачи вращательного движения (рис. 4.14, в), с упругостью С, моментом инерции ] и коэффициентом скоростного трения 5, гироскопические элементы (рис. 4.14, г) и др.
Рассмотрим для иллюстрации гироскопический элемент (рис. 4.14, г). В качестве входной величины примем момент М, прикладываемый к оси а, а в качестве выходной — угол поворота этой же оси.
Уравнение равновесия моментов на оси
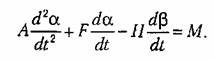
Будем считать, что на оси р (оси прецессии) не действуют никакие внешние моменты. Тогда для этой оси уравнение равновесия моментов запишется так:
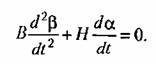
кинетический
 — коэффициент скоростного сопротивления на оси а. — коэффициент скоростного сопротивления на оси а.
Переходя к операторным выражениям и решая оба уравнения совместно, получаем:
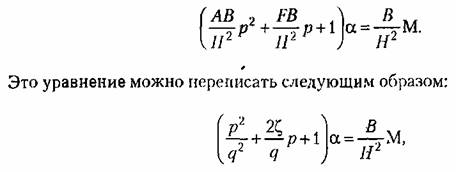
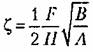 — —
параметр затухания, определяемый действием сил скоростного трения па оси а. Это уравнение совпадает с выражением (4.32).
Для решения дифференциального уравнения (4.31) или (4.32) необходимо найти корни характеристического уравнения
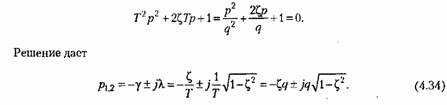
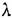 — частоту затухающих колебаний. — частоту затухающих колебаний.
Временные характеристики звена приведены в табл. 4,2, а частотные характеристики — в табл. 4.3.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
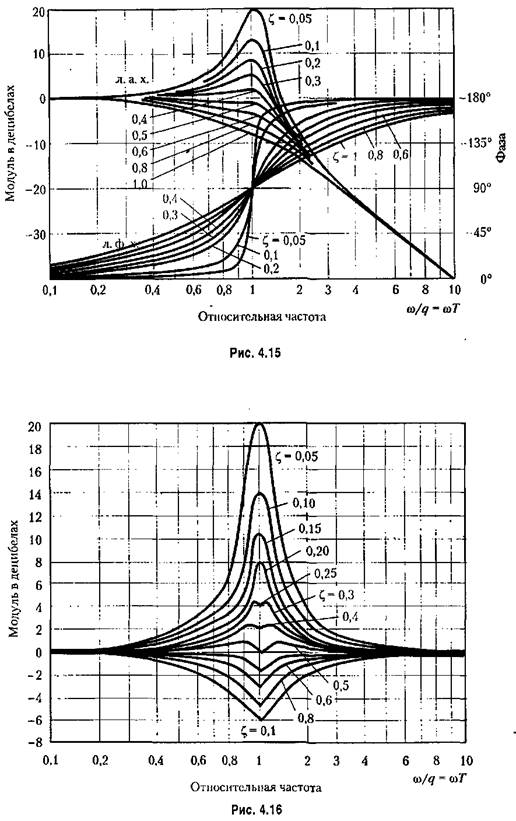
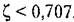 . Высота пика будет тем больше, чем меньше параметр затухания: . Высота пика будет тем больше, чем меньше параметр затухания:
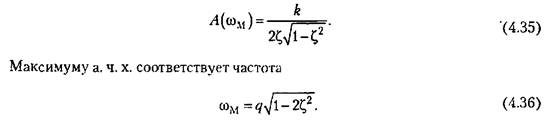
Л. а. х. строится по выражению
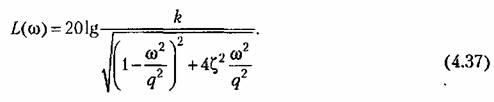
Однако построение л. а. х. не может быть сделано так просто, как это было для предыдущих звеньев. Для построения используются так называемые нормированные л. а. х. Постоянный множитель под знаком логарифма в выражении (4.37) может быть выделен в отдельное слагаемое:
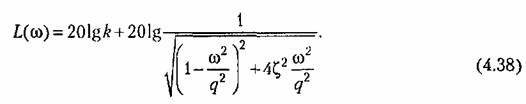
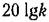 и по оси частот от относительной частоты перейти к действительной умножением на д. и по оси частот от относительной частоты перейти к действительной умножением на д.
В функции той же относительной частоты на рис. 4.15 нанесены нормированные л. ф. х., построенные по выражению

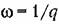 с последующим введением поправки, которая приведена на рис. 4.16. с последующим введением поправки, которая приведена на рис. 4.16.
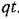
 приводит к повышению колебательности переходного процесса и росту резонансного пика амплитудной частотной характеристики. приводит к повышению колебательности переходного процесса и росту резонансного пика амплитудной частотной характеристики.
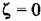 . Тогда передаточная функция (4.33) будет иметь вид . Тогда передаточная функция (4.33) будет иметь вид
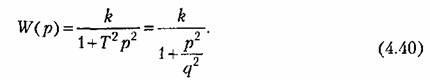
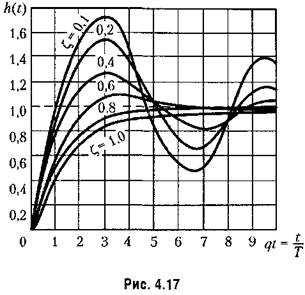

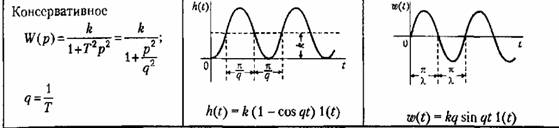
Временные характеристики соответствуют незатухающим колебаниям (табл. 4.2) с угловой частотой q
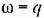 модуль частотной передаточной функции обращается в бесконечность, а фаза делает скачок на 180°. модуль частотной передаточной функции обращается в бесконечность, а фаза делает скачок на 180°.
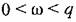 характеристика совпадает с положительной полуосью. характеристика совпадает с положительной полуосью.
|