Теория систем автоматического управленияНеустойчивые и минимально-фазовые звенья
Рассмотренные выше звенья позиционного типа относятся к устойчивым звеньям, или к звеньям с самовыравпиванием. Под самовыравниванием понимается способность звена самопроизвольно приходить к новому установившемуся состоянию при ограниченном изменении входной величины или возмущающего воздействия. Термин самовыравпившше обычно применяется для звеньев, представляющих собой объекты управления.
Существуют звенья, у которых ограниченное изменение входной величины или возмущающего воздействия не вызывает прихода звена к новому установившемуся состоянию, а выходная величина имеет тенденцию неограниченного возрастания во времени. К таким звеньям относятся, например, звенья интегрирующего типа. Они были рассмотрены выше.
Существуют звенья, у которых этот процесс выражен еще заметнее. Это объясняется наличием положительных вещественных корней или комплексных корней с положительной вещественной частью в характеристическом уравнении, в результате чего звено будет относиться к категории неустойчивых звеньев. Вопрос устойчивости будет изложен подробно в главе 6. Рассмотрим в качестве примера звено, описываемое дифференциальным уравнением

которому соответствует передаточная функция

Переходная функция такого звена представляет собой показательную функцию с положительным показателем степени:
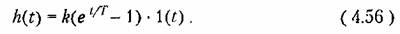
Эта функция изображена на рис. 4.22.
 , имеет положительный наклон. На рис. 4.23 изображены разновидности механических характеристик двигателя. В случае, соответствующем кривой У, двигатель представляет собой устойчивое апериодическое звено первого порядка, уравнения движения , имеет положительный наклон. На рис. 4.23 изображены разновидности механических характеристик двигателя. В случае, соответствующем кривой У, двигатель представляет собой устойчивое апериодическое звено первого порядка, уравнения движения

которого были рассмотрены в § 4.5. Это звено имеет положительное самовыравнивание.
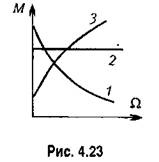
В случае, соответствующем кривой 2, когда вращающий момент не зависит от скорости вращения, уравнение движения двигателя, записанное для угловой скорости, приобретает вид

 и вращающим моментом. Здесь скорость двигателя связана с управляющим воздействием передаточной функцией, соответствующей интегрирующему звену и вращающим моментом. Здесь скорость двигателя связана с управляющим воздействием передаточной функцией, соответствующей интегрирующему звену
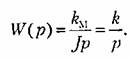
Это звено не имеет самовыравнивания. В случае, соответствующем кривой 3, дифференциальное уравнение движения будет

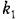 — наклон механической характеристики в точке, где производится линеаризация. Это уравнение приводится к следующему виду: — наклон механической характеристики в точке, где производится линеаризация. Это уравнение приводится к следующему виду:

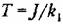 — постоянная времени двигателя. — постоянная времени двигателя.
Уравнение совпадает с выражением (4.54). Звено имеет отрицательное самовыравнивание.
Признаком отрицательного самовыравнивания является отрицательный знак перед самой выходной величиной в левой части дифференциального уравнения (см., например, формулу (4.54)) или появление отрицательного знака у свободного члена знаменателя передаточной функции (см., например, формулу (4.55)).
Существенной особенностью неустойчивых звеньев является наличие больших но сравнению с устойчивыми звеньями фазовых сдвигов. Так, для рассматриваемого апериодического звена с отрицательным самовыравниванием (неустойчивого) частотная передаточная функция на основании (4.55) будет равна

Модуль ее не отличается от модуля частотной передаточной функции устойчивого апериодического звена (табл. 4.3):

Поэтому а. ч. х. и л. а. х. этих двух звеньев (устойчивого и неустойчивого) совпадают и по одной амплитудной характеристике нельзя определить, к какому звену она относится.
Фазовый сдвиг, соответствующий неустойчивому апериодическому звену
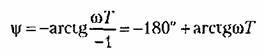
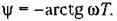
В связи с этим неустойчивые звенья относятся к группе так называемых пемипи-малыш-фазовых звеньев, поскольку минимальные по абсолютному значению фазовые сдвиги при одинаковых амплитудных характеристиках будут у устойчивых звеньев. К неминимально-фазовым звеньям относятся также устойчивые звенья, имеющие в числителе передаточной функции (в правой части дифференциального уравнения) вещественные положительные корни или комплексные корни с положительной вещественной частью. Например, звено с передаточной функцией
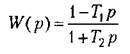
относится к группе неминимально-фазовых звеньев. Действительно, по сравнению со звеном, имеющим передаточную функцию

оно будет иметь большие по абсолютной величине фазовые сдвиги, так как

при одинаковом виде амплитудно-частотной характеристики.
Напомним, что к мипимальпо-фазовым звеньям относятся такие, у которых корни числителя и знаменателя передаточной функции находятся в левой полуплоскости (см. §4.3).
К неустойчивым звеньям, кроме рассмотренного выше звена, относятся также следующие звенья с соответствующими передаточными функциями:
квазикоисервативное звено —

квазиколебателыюе звено —

колебательное звено с отрицательным затуханием -

и ряд других звеньев.
Наличие в автоматической системе неустойчивых звеньев вызывает некоторые особенности расчета, которые будут рассмотрены ниже.
|