Теория систем автоматического управленияСоставление исходных дифференциальных уравнений
Составление исходных дифференциальных уравнений систем автоматического управления
Общий метод составления исходных уравнений
Система автоматического управления состоит из взаимосвязанных и взаимодействующих между собой управляемого объекта и управляющего устройства (см. рис. 1.2). Поэтому для получения дифференциального уравнения всей системы необходимо составить уравнения для каждого из них.
При составлении дифференциального уравнения объекта необходимо прежде всего выявить физический закон (или совокупность законов), определяющий его поведение. Таким законом может быть, например, закон сохранения энергии, закон равновесия электродвижущих сил и другие основные законы физики. Математическое выражение соответствующего физического закона и является исходным дифференциальным уравнением управляемого объекта.
Например, для составления дифференциального уравнения электродвигателя, являющегося управляемым объектом для системы стабилизации скорости вращения (рис. 1.14), используется закон равновесия моментов на его валу, который может быть записан в следующем виде:

 . — тормозной момент внешних сил (момент нагрузки), являющийся для данного объекта возмущающим воздействием. . — тормозной момент внешних сил (момент нагрузки), являющийся для данного объекта возмущающим воздействием.
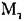 . Нужно также выяснить, является ли приведенный момент инерции постоянной величиной или он изменяется в функции какой-либо переменной. . Нужно также выяснить, является ли приведенный момент инерции постоянной величиной или он изменяется в функции какой-либо переменной.
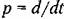 можно представить в виде можно представить в виде
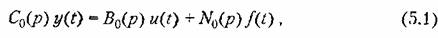
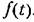

 . В зависимости от знаков вещественных частей корней этого полинома объект может быть устойчивым или неустойчивым (см. § 4.8). . В зависимости от знаков вещественных частей корней этого полинома объект может быть устойчивым или неустойчивым (см. § 4.8).

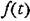 на характер изменения управляемой величины. на характер изменения управляемой величины.
Управляющее устройство, как показано на рис. 1.3; состоит из различных элементов или звеньев. Уравнения некоторых из них известны заранее. Например, для следящей системы (рис. 1.15) датчик угла рассогласования может быть представлен безынерционным звеном, т. е.
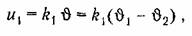
усилитель — апериодическим звеном первого порядка, т. е.
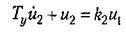
и т. д.
Для другой группы элементов дифференциальные уравнения составляются аналогично тому, как это делалось для управляемого объекта.
 В результате получается дифференциальное уравнение управляющего устройства В результате получается дифференциальное уравнение управляющего устройства


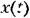
В первом случае получается дифференциальное уравнение
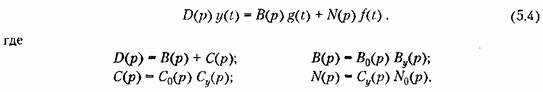
 порядка характеризует свободное движение системы автоматического управления. Он называется характеристическим полиномом замкнутой системы и может быть представлен в виде порядка характеризует свободное движение системы автоматического управления. Он называется характеристическим полиномом замкнутой системы и может быть представлен в виде
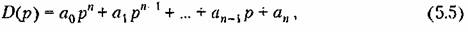
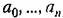 в линеаризованной системе представляют собой постоянные коэффициенты. в линеаризованной системе представляют собой постоянные коэффициенты.
 отличается от характеристического полинома отличается от характеристического полинома
 . Это означает, что и свободное движение системы может существенно . Это означает, что и свободное движение системы может существенно
отличаться от свободного движения объекта. В частности, .если управляемый объект неустойчив, то при правильно выбранных алгоритме управления и параметрах управляющего устройства система в целом будет устойчивой. Наоборот, при неправильном выборе система автоматического управления устойчивым объектом может стать неустойчивой.

 , причем последняя должна как можно более точно воспроизводить задающее воздействие, т. е. ошибка системы (5.3) должна быть минимальной. , причем последняя должна как можно более точно воспроизводить задающее воздействие, т. е. ошибка системы (5.3) должна быть минимальной.
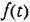 характер характер
 . В принципе таких возмущений может быть несколько. Однако вследствие линейности уравнения действует принцип суперпозиции, согласно которому реакция на сумму воздействий равна сумме реакции. Поэтому достаточно рассмотреть методику учета только одного возмущения, а при наличии нескольких возмущений необходимо лишь просуммировать результат. . В принципе таких возмущений может быть несколько. Однако вследствие линейности уравнения действует принцип суперпозиции, согласно которому реакция на сумму воздействий равна сумме реакции. Поэтому достаточно рассмотреть методику учета только одного возмущения, а при наличии нескольких возмущений необходимо лишь просуммировать результат.
 дифференциальное уравнение системы может быть получено подстановкой в (5.4) выражения для ошибки (5.3): дифференциальное уравнение системы может быть получено подстановкой в (5.4) выражения для ошибки (5.3):

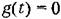
 Это означает, что выбором структуры и пара- Это означает, что выбором структуры и пара-
 означает, что система инвариантна относительно задающего воздействия. означает, что система инвариантна относительно задающего воздействия.
Уравнения (5.1), (5.4) и (5.6) могут быть также представлены в виде совокупности уравнений первого порядка, называемых уравнениями состояния. Они рассматриваются в § 5.5.
|