Теория систем автоматического управленияОбщие сведения об устойчивости
Устойчивость является одним из главных требований, предъявляемых к автоматическим системам.
 ), то он возвратится к точке Л0. Состояние равновесия в точке Л0 на рис. 6.1, а неустойчиво. ), то он возвратится к точке Л0. Состояние равновесия в точке Л0 на рис. 6.1, а неустойчиво.
В этом примере, как и в теории устойчивости, полагается, что внешние силы или возмущения прекращают свое действие к некоторому моменту времени, который можно принять за начальный момент I = 0. Такие возмущения часто называют исчезающими.
Применительно к системам автоматического управления такое понятие устойчивости можно использовать лишь частично для характеристики свойств их объектов, которые сами по себе могут быть устойчивыми или неустойчивыми. К последним относятся, например, некоторые ракеты.
Автоматические системы отличаются тем, что в них, во-первых, осуществляется специально организованное управление объектом. Благодаря ему система с неустойчивым объектом может стать устойчивой, а система с устойчивым объектом (при неправильном управлении) — неустойчивой. Так, неустойчивое состояние равновесия шара на рис. 6.1, б легкими прикосновениями можно сделать устойчивым, а шар на рис. 6.1, а тем же способом можно раскачать так, что амплитуда колебаний будет увеличиваться.
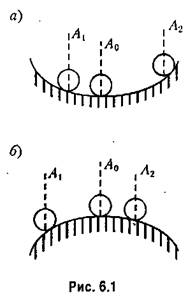
Во-вторых, при наличии исчезающих задающего и возмущающих воздействий система может иметь много состояний равновесия. Так, система стабилизации напряжения в электрической сети при номинальном токе нагрузки (возмущающем воздействии) поддерживает заданное значение напряжения, а при увеличении тока нагрузки из-за подключения дополнительных потребителей переходит в другое состояние равновесия, отличающееся пониженным значением напряжения.
В-третьих, для ряда систем типичным режимом работы является движение. Так, исполнительная ось следящей системы в процессе слежения движется с постоянной или переменной угловой скоростью, закон изменения которой в общем случае может быть случайным. Состояние равновесия можно рассматривать как простейший частный случай движения.
В классической теории устойчивости исследуется не устойчивость системы как таковой, а устойчивость ее так называемого невозмущенного движения.
Ниже будет показано, что для линейных систем с точки зрения устойчивости не имеет значения, какое их движение принимается в качестве невозмущенного. Это может быть, например, состояние равновесия системы стабилизации напряжения при любом (даже не заданном)токе нагрузки или движение исполнительной оси следящей системы по случайному закону. Однако для нелинейных систем это имеет существенное значение, так как одно конкретно заданное невозмущенное движение может оказаться устойчивым, а другое — неустойчивым.
 возмущения вызывают отклонение движения системы от ее невозмущенного движения. Это новое движение называется возмущенным. возмущения вызывают отклонение движения системы от ее невозмущенного движения. Это новое движение называется возмущенным.
Строгая математическая теория устойчивости была создана Л. И. Ляпуновым и изложена мм в работе Общая задача об устойчивости движения, опубликованной в 1892 г. В ней было определено понятие устойчивости и разработаны методы устойчивости нелинейных систем.
 изменяются, а точка М прочерчивает некоторую траекторию. изменяются, а точка М прочерчивает некоторую траекторию.

 возмущения возмущения

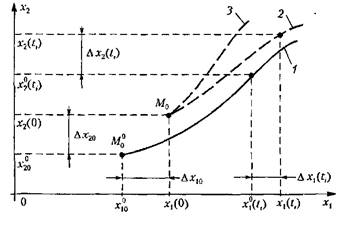
Рис. 6.2

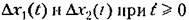 остаются малыми (кривая 2). остаются малыми (кривая 2).
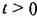 не остается малым (кривая 3). не остается малым (кривая 3).

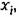 соответственно, столько же начальных и текущих отклонений. соответственно, столько же начальных и текущих отклонений.
Определим теперь понятие устойчивости более четко.
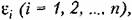 как бы мало оно ни было, как бы мало оно ни было,
 такое, что при любых начальных отклонениях, удовлетворяющих условиям такое, что при любых начальных отклонениях, удовлетворяющих условиям
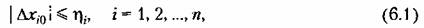
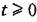 удовлетворяют условиям удовлетворяют условиям

Невозмущенное движение называется асимптотически устойчивым, если оно
устойчиво по Ляпунову п, кроме того,

Смысл условий (6.1) рассмотрим на примере системы второго порядка.
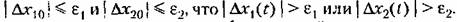 Условия (6.1), таким образом, устанавливают, что необходимо найти такое сочетание начальных отклонений и их предельных значений, при которых условия (6.2) выполняются. Условия (6.1), таким образом, устанавливают, что необходимо найти такое сочетание начальных отклонений и их предельных значений, при которых условия (6.2) выполняются.
Понятие устойчивости по Ляпунову широко используется при исследовании нелинейных систем (см. гл. 16 н 17). Для линейных систем имеет смысл, как будет показано ниже, только понятие асимптотической устойчивости.
Уравнения состояния линейной системы можно представить в виде
 ) )
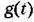 Аналогичным будет и решение этих уравнений: Аналогичным будет и решение этих уравнений:

 воздействий. Второе слагаемое воздействий. Второе слагаемое
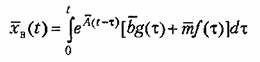
представляет собой частное решение неоднородного уравнения (6.4) и называется вынужденной составляющей. Она характеризует то движение системы, которое ее вынуждает совершать задающее и возмущающее воздействия.

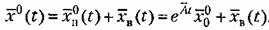
 Заменив в (6.5) Заменив в (6.5)
 отклонениями, получим; отклонениями, получим;

 будет устойчивым, если устойчиво свободное движение будет устойчивым, если устойчиво свободное движение
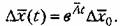
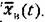 В этом случае из (6.5) сразу следует, что оно устойчиво, если устойчиво свободное движение (6.6). В этом случае из (6.5) сразу следует, что оно устойчиво, если устойчиво свободное движение (6.6).
Сделаем теперь общие для всех линейных систем (замкнутых, разомкнутыхили только управляемых объектов) выводы.
Устойчивость невозмущешюго движения не зависит от того, какое движение системы принято в качестве певозмущенного.
Певозмущенное движение системы устойчиво, если устойчиво ее свободное движение.
Устойчивость невозмущенного движения не зависит от вида и характера изменения внешних (задающего и возмущающих) воздействий. Этот вывод базируется на двух предыдущих.
В дальнейшем для краткости устойчивость певозмущпепого движения будем называть просто устойчивостью системы.
 С то- С то-
точки зрения устойчивости, как показано выше, нас интересует только переходная составляющая, т. е. общее решение дифференциального уравнения

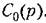
Решение уравнения (6,8), как известно, представляется в виде

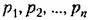 — некратные корни характеристического уравнения — некратные корни характеристического уравнения

 Поэтому в соответствии с (6.3) система будет асимптотически устойчивой, если Поэтому в соответствии с (6.3) система будет асимптотически устойчивой, если

Это условие выполняется, если каждая из составляющих решения (6.9) с течением времени стремится к нулю.
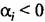
 непрерывно нарастают. непрерывно нарастают.
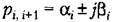 соответствует пара составляющих, сумму которых, как известно, можно представить в виде соответствует пара составляющих, сумму которых, как известно, можно представить в виде
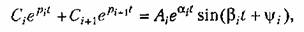
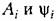 — новые произвольные постоянные. Вызванный этими корнями колеба- — новые произвольные постоянные. Вызванный этими корнями колеба-
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение

Таким образом, затухание или незатухание переходной составляющей (6.9) зависит только от знаков вещественных корней и знаков вещественных частей комплексных корней характеристического уравнения.
Для асимптотической устойчивости системы необходимо и достаточно, чтобы вещественные части корней были отрицательными:

При этом вещественные корпи рассматриваются как мастный случай комплексных корней, у которых мнимая часть равна пулю.
Нетрудно убедиться, что в этом случае наряду с (6.10) выполняются и условия (6.1) и (6.2).
Если хотя бы один корень имеет положительную вещественную часть, то система неустойчива.
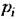 (рис. 6.3). Для устойчивости системы необходимо и достаточно, чтобы псе корни находились па левой полуплоскости (рис. 6.3, а). Если хотя бы один вещественный корень или хотя бы (рис. 6.3). Для устойчивости системы необходимо и достаточно, чтобы псе корни находились па левой полуплоскости (рис. 6.3, а). Если хотя бы один вещественный корень или хотя бы

одна пара комплексных корней окажутся на правой полуплоскости (рис. 6.3, б), то система будет неустойчивой. Таким образом, левая полуплоскость является областью устойчивости, а мнимая ось представляет собой ее границу.
В тех случаях, когда на эту границу попадает хотя бы один корень, а все остальные остаются на левой полуплоскости, система оказывается в некотором промежуточном состоянии между устойчивостью и неустойчивостью. Для характеристики этого состояния вводится понятие границы устойчивости.

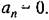 Но чтобы это условие соответствовало апериодической границе устойчивости, все корпи уравнения Но чтобы это условие соответствовало апериодической границе устойчивости, все корпи уравнения
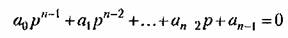
должны находиться на левой полуплоскости.
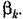
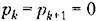 соответствующая им сумма составляющих решения (6,9), как известно, представляется в виде соответствующая им сумма составляющих решения (6,9), как известно, представляется в виде

 она неограниченно увеличивается. Поэтому в данном случае систему следует рассматривать как неустойчивую. она неограниченно увеличивается. Поэтому в данном случае систему следует рассматривать как неустойчивую.
Все сделанные выше выводы об устойчивости относятся к линейным системам. Однако реальные системы практически никогда не бывают строго линейными. Линейные дифференциальные уравнения получаются путем линеаризации, в процессе которой малые нелинейные члены отбрасываются.
Линеаризованными уравнениями, или уравнениями первого приближения стали пользоваться еще в середине XIX века, предполагая, что по ним можно судить об устойчивости реальных систем. Строгое доказательство такой возможности было дано Ляпуновым.
Ляпунов показал, что если в характеристическом уравнении нет пулевых и чисто мнимых корней (см, рис. 6.3, а и рис. 6.3, б), то вопрос об устойчивости или неустойчивости реальной системы полностью решается на основе этого уравнения. Однако при наличии таких корней (см. рис. 6.3, в и рис. 6.3, г) поведение реальной системы становится неопределенным, т, е. в зависимости от отброшенных при линеаризации малых нелинейных членов она может быть как устойчивой, так и неустойчивой.
Применительно к рис. 6.3, в и рис. 6.3, г это означает, что изображенные на них процессы относятся только к строго линейным системам. Тем не менее само понятие границы устойчивости оказывается полезным и будет использоваться в дальнейшем.
Следует учитывать, что выводы Ляпунова относятся только к описанному в гл. 3 способу линеаризации и справедливы при сделанных там допущениях. Для исследования устойчивости нелинейных систем общего вида Ляпунов разработал другие методы, которые будут рассмотрены в гл. 16 и гл. 17.
Задача вычисления корней характеристического уравнения любого порядка при помощи средств вычислительной техники решается достаточно просто, если параметры элементов системы (коэффициенты передачи, постоянные времени) и тем самым коэффициенты этого уравнения заданы численно. На практике, однако, обычно пользуются так называемыми критериями устойчивости, т. е. правилами, которые позволяют судить об устойчивости без вычисления корней. Ценность этих критериев состоит не только и даже не столько в том, что устраняется необходимость вычисления корней. Они дают возможность установить, как тот или иной параметр и структура системы в целом влияют на устойчивость и как их следует изменить, чтобы система стала устойчивой.
Наиболее простым, хотя и ограниченным но своим возможностям критерием является необходимое условие устойчивости.
Необходимым (но не достаточным) условием устойчивости системы является положительность коэффициентов ее характеристического уравнения.
Это значит, что при положительности всех коэффициентов система может быть устойчивой, но не исключается возможность ее неустойчивости. Окончательный вывод можно сделать применив, например, критерий Гурвица (см. § 6.2). Если же не все коэффициенты положительны, то система наверняка не может быть устойчивой и никаких дополнительных исследований не требуется.
Необходимость положительности всех коэффициентов характеристического уравнения системы любого порядка устанавливает критерий Гурвица. Для систем первого и второго порядков необходимое условие является и достаточным, в чем нетрудно убедиться прямым нахождением корней уравнения.
Исследование устойчивости любой системы всегда полезно начинать с проверки выполнения необходимого условия. В качестве иллюстрации рассмотрим три примера.
Система второго порядка, характеристическое уравнение которой

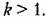
Система третьего порядка, характеристическое уравнение которой

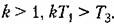
Система, характеристическое уравнение которой
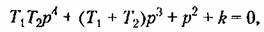
 и не может стать положительным ни при каких значениях параметров. Для обеспечения устойчивости такой системы необходимо изменить ее структуру, например, за счет введения корректирующих звеньев, что приведет к изменению характеристического уравнения. и не может стать положительным ни при каких значениях параметров. Для обеспечения устойчивости такой системы необходимо изменить ее структуру, например, за счет введения корректирующих звеньев, что приведет к изменению характеристического уравнения.
|