Теория систем автоматического управленияПостроение областей устойчивости. D-разбиение
При расчете и проектировании системы автоматического управления иногда бывает необходимым исследовать влияние ее различных параметров па устойчивость. Для решения этой задачи служит построение областей устойчивости, т. е. определение
таких областей значений параметров, при которых система оказывается устойчивой.
Различают построение областей устойчивости в плоскости одного параметра и в
плоскости двух параметров. Ниже будет рассматриваться только построение областой устойчивости в плоскости двух параметров. Для построения таких областей ш плоскости двух параметров A и B необходимо нанести линии, соответствующие границе устойчивости. Тогда область, ограниченная этими линиями, будет представлять собой область устойчивости. Для того чтобы окончательно убедиться в этом необходимо для любой точки, лежащей внутри полученной области, но какому-л ибс критерию проверить устойчивость. Если устойчивость для этой точки будет иметь место, то она будет выполняться и для всех других точек, лежащих в этой области.
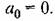
Для получения условия, соответствующего границе устойчивости второго типе (колебательной), можно использовать различные критерии устойчивости.

Для уравнений высокого порядка условия, соответствующие колебательной границе устойчивости, могут быть получены следующим образом.
Рассмотрим отдельно левую часть характеристического уравнения (6.9), которая представляет собой характеристический полином замкнутой системы:

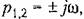 где где
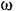 — угловая частота колебаний, соответствующая чисто мнимому корню. Тогда лузрактеристический комплекс — угловая частота колебаний, соответствующая чисто мнимому корню. Тогда лузрактеристический комплекс
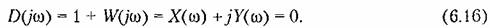
 распадается на два уравнения: распадается на два уравнения:

Два последних выражения представляют собой параметрические уравнения границы устойчивости при соблюдении дополнительного условия отрицательности вещественных частей всех остальных корней, кроме чисто мнимых. Полная же совокупность всех кривых па плоскости параметров, разбивающая всю плоскость на области с определенным распределением корней, называется D-разбиеиием плоскости параметров. Обычно практическое значение имеет лишь часть кривых D-разбиеиия, соответствующая границе устойчивости.
Для упрощения выделения границ области устойчивости из всего комплекса кривых D-разбиения на плоскости двух параметров вводится штриховка этих кривых, производимая по правилу, которое будет приведено без доказательства. Переметаясь вдоль кривой в сторону увеличения со, надо штриховать ее с левой стороны, если будет положительным определитель, составленный из частных производных (6.17):

Если же определитель отрицателен, то кривую надо штриховать справа. При соблюдении этого правила штриховка будет направлена внутрь области устойчивости, если параметр Л отложен но оси абсцисс вправо, а параметр В — по оси ординат вверх.
В качестве иллюстрации рассмотрим следящую систему, схема которой изображена на рис. 6.4. Для этой системы было получено характеристическое уравнение
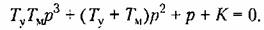

Характеристический комплекс

Уравнения, определяющие границу устойчивости,

Решая их совместно относительно параметров К и Т, получим

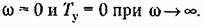
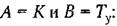
 I I

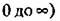 необходимо штриховать область, лежащую справа от кривой. необходимо штриховать область, лежащую справа от кривой.
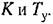
Это можно показать и на основе использования двух оставшихся условий устойчивости.

 Это условие выполняется на оси абсцисс. Это условие выполняется на оси абсцисс.
 можно сразу ответить, устойчива или неустойчива система, смотря по тому, попадает или не попадает точка, определяемая этими значениями параметров, в область устойчивости. можно сразу ответить, устойчива или неустойчива система, смотря по тому, попадает или не попадает точка, определяемая этими значениями параметров, в область устойчивости.
Для системы угловой стабилизации, структурная схема которой изображена па рис. 6.5, область устойчивости представлена на рис. 6.7.
|