Теория систем автоматического управленияОпределение устойчивости по логарифмическим частотным характеристикам
Для определения устойчивости по критерию Найквиста можно строить не амплитудно-фазовую характеристику, а логарифмическую амплитудную частотную характеристику (л. а. х.) и логарифмическую фазовую частотную характеристику (л. ф. х.) разомкнутой системы.
Построение л. а. х. производится по выражению

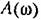 - модуль частотной передаточной функции разомкнутой системы (6.23). - модуль частотной передаточной функции разомкнутой системы (6.23).
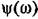 частотной передаточной функции (6.23). Для построения л. а. х. и л. ф. х. удобно использовать стандартную сетку, изображенную на рис. 4.19. частотной передаточной функции (6.23). Для построения л. а. х. и л. ф. х. удобно использовать стандартную сетку, изображенную на рис. 4.19.
Наиболее простое построение получается, если передаточную функцию разомкнутой системы можно свести к виду
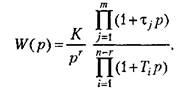
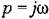 получаем получаем

Фаза (аргумент) частотной передаточной функции

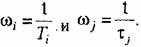 разомкнутой системы разомкнутой системы

которой соответствует выражение для модуля в логарифмическом масштабе
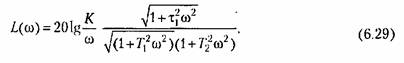
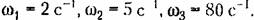

 находящуюся па 20 дБ выше оси абсцисс. находящуюся па 20 дБ выше оси абсцисс.
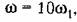 точка Л опустится па 40 дБ. точка Л опустится па 40 дБ.
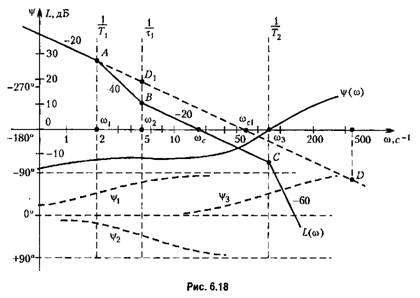
 сомножителя второго порядка знаменателя (6.28), то л. а. х. изламываем на -40 дБ/дек и последняя асимптота будет иметь наклон -60 дБ/дек. сомножителя второго порядка знаменателя (6.28), то л. а. х. изламываем на -40 дБ/дек и последняя асимптота будет иметь наклон -60 дБ/дек.
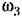 — на 6 дБ ниже асимптотической. — на 6 дБ ниже асимптотической.
Выражение для фазы (6.28) имеет вид
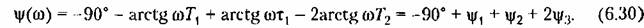
 (см. рис. 6.18). Все остальные получаются простым сдвигом этой фазовой характеристики так, чтобы па соответствующей сопрягающей частоте иметь фазовый сдвиг 45°. При этом необходимо учитывать знак каждого слагаемого (6.30). Логарифмическая фазовая характеристика (рис. 6.18) получается в результате алгебраического суммирования всех слагаемых (6.30). Построение л. ф. х. можно существенно упростить, если заранее будет подготовлен шаблон для одной из указанных зависимостей. (см. рис. 6.18). Все остальные получаются простым сдвигом этой фазовой характеристики так, чтобы па соответствующей сопрягающей частоте иметь фазовый сдвиг 45°. При этом необходимо учитывать знак каждого слагаемого (6.30). Логарифмическая фазовая характеристика (рис. 6.18) получается в результате алгебраического суммирования всех слагаемых (6.30). Построение л. ф. х. можно существенно упростить, если заранее будет подготовлен шаблон для одной из указанных зависимостей.
Аналогичное построение л. а. х. и л. ф. х. может быть сделано при любом значении г. Разница будет заключаться в наклоне первой асимптоты л. а. х. и величине первого слагаемого выражения для фазы (6.27).
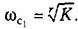
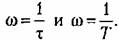 На первой л. а. х. На первой л. а. х.
 в асимптотическую л. а. х. следует внести поправки в соответствии с рис. 4.15 или рис. 4.16 (для первого из указанных сомножителей они берутся с обратным знаком). в асимптотическую л. а. х. следует внести поправки в соответствии с рис. 4.15 или рис. 4.16 (для первого из указанных сомножителей они берутся с обратным знаком).
Аналогично изложенному выше строится и л. ф. х. Для построения составляющих фазовой характеристики, соответствующих сомножителям с комплексными корнями, можно использовать графики, приведенные на рис. 4.15.
Обратимся теперь к исследованию устойчивости замкнутой системы но построенным л. а. х. и л. ф. х. разомкнутой системы. Для этого воспользуемся последней из приведенных выше формулировок критерия Найквиста, связанной с прохождением а. ф. х. через критический отрезок.
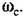
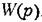 . Как и прежде, переход сверху вниз считается положительным, а снизу вверх — отрицательным. . Как и прежде, переход сверху вниз считается положительным, а снизу вверх — отрицательным.
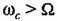 появится -1 переход через критический отрезок и замкнутая система станет неустойчивой. появится -1 переход через критический отрезок и замкнутая система станет неустойчивой.
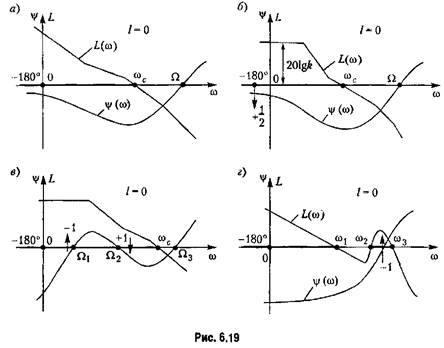
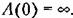
 и сумма переходов равна нулю. и сумма переходов равна нулю.
 Так как имеется -1 переход через вторую часть критического отрезка, то замкнутая система неустойчива. Так как имеется -1 переход через вторую часть критического отрезка, то замкнутая система неустойчива.
Большое практическое преимущество критерия Найквиста состоит в том, что а. ф. х. или л. ч. х. разомкнутой системы могут быть получены не только расчетным путем (в том числе и с использованием средств вычислительной техники) при заданной передаточной функции разомкнутой системы, но и сняты экспериментально при наличии уже созданных автоматической системы в целом или отдельных ее устройств. Это особенно важно тогда, когда достоверность исходных дифференциальных уравнений но тем или иным причинам вызывает сомнение.
|