Теория систем автоматического управленияУстойчивость систем с запаздыванием
Системы с запаздыванием отличаются от рассмотренных ранее систем тем, что в одном или нескольких из своих звеньев имеют запаздывание во времени начала изменения выходной величины (после начала изменения входной) на величину т, называемую временем запаздывания, причем это время запаздывания остается постоянным и во всем последующем ходе процесса.
Например, если звено описывается уравнением

(апериодическое звено первого порядка), то уравнение соответствующего звена с запаздыванием будет иметь вид
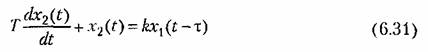
(апериодическое звено первого порядка с запаздыванием). Такого вида уравнения называются уравнениями с запаздывающим аргументом,
 Тогда уравнение (6.31) запишется в обыкновенном Тогда уравнение (6.31) запишется в обыкновенном
виде:

 изменяется скачком от нуля до единицы (рис. 6.20, изменяется скачком от нуля до единицы (рис. 6.20,
 стоящей в правой части уравнении звена, стоящей в правой части уравнении звена,
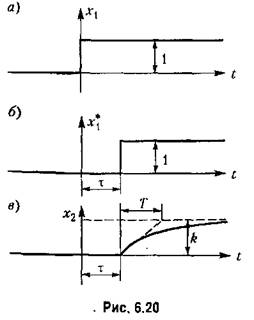
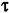 ). В общем случае, как и для (6.31), уравнение динамики любого звена с запаздыванием можно разбить на два: ). В общем случае, как и для (6.31), уравнение динамики любого звена с запаздыванием можно разбить на два:
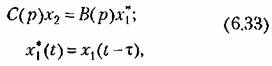
что соответствует условной разбивке звена с запаздыванием (рис. 6.21, а) па два: обыкновенное звено того же порядка и с теми же коэффициентами и предшествующий ему элемент запаздывания (рис. 6.21,6).

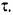
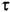 означает время движения металла от валков до измерителя толщины. В двух последних примерах величина т называется транспортным запаздыванием. означает время движения металла от валков до измерителя толщины. В двух последних примерах величина т называется транспортным запаздыванием.
В первом приближении определенной величиной запаздывания т могут быть охарактеризованы трубопроводы или длинные электрические линии, входящие в звенья системы.
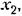 показанная на рис. 6.22, б, то можно приближенно описать это звено как апериодическое звено первого порядка с запаздыванием (6.31), взяв величины т, Г и к с экспериментальной кривой (рис, 6,22, б). показанная на рис. 6.22, б, то можно приближенно описать это звено как апериодическое звено первого порядка с запаздыванием (6.31), взяв величины т, Г и к с экспериментальной кривой (рис, 6,22, б).
Заметим также, что такая же экспериментальная кривая согласно графику рис. 6.22, в может трактоваться и как временная характеристика обыкновенного апериодического звена второго порядка с уравнением

 и к можно вычислить из соотношений, записанных в § 4.5 для данного звена, по некоторым замерам на экспериментальной кривой или другими способами. и к можно вычислить из соотношений, записанных в § 4.5 для данного звена, по некоторым замерам на экспериментальной кривой или другими способами.


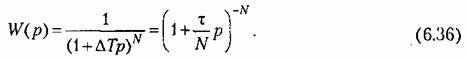

функция (6.36) мало отличается от передаточной функции звена с запаздыванием (6.35).
Уравнение любого линейного звена с запаздыванием (6.33) будем теперь записывать в виде

Передаточная функция линейного звена с запаздыванием будет
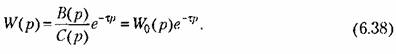
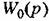 обозначена передаточная функция соответствующего обыкновенного звена без запаздывания. обозначена передаточная функция соответствующего обыкновенного звена без запаздывания.
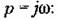
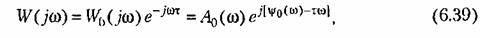
 — модуль и фаза частотной передаточной функции звена без запаздывания. — модуль и фаза частотной передаточной функции звена без запаздывания.

Отсюда получаем следующее правило.
Для построения амплитудно-фазовой характеристики любого звена с запаздыванием нужно взять характеристику соответствующего обыкновенного звена и каждую ее точку сдвинуть вдоль окружности по часовой стрелке на угол то, где со — значение частоты колебаний в данной точке характеристики (рис. 6.23, а).
 то то
начальная точка остается без изменения, а конец характеристики асимптотически навивается на начало координат (если степень операторного многочлена В меньше, чем многочлена С).
Выше говорилось о том, что реальные переходные процессы (временные характеристики) вида рис. 6.22, б часто могут быть с одинаковой степенью приближения описаны как уравнением (6.31), так и (6.34). Амплитудно-фазовые характеристики для уравнений (6.31) и (6.34) показаны на рис. 6.23, а и б соответственно. Принципиальное отличие первой состоит в том, что она имеет точку D пересечения с осью (/. При сравнении обеих характеристик между собой и с экспериментальной амплитудно-фазовой характеристикой реального звена надо принимать во внимание не только форму кривой, но и характер распределения отметок частот со вдоль нее.
 — передаточная функция разомкнутой системы без запаздывания. — передаточная функция разомкнутой системы без запаздывания.
Характеристическое уравнение замкнутой системы, как показано в гл. 5, имеет вид
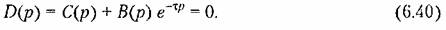
 уравнение может иметь бесконечное количество корней. уравнение может иметь бесконечное количество корней.
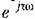 существенно изменяется очертание амплитудно-фазовой характеристики разомкнутой цени, построенной но частотной передаточной функции существенно изменяется очертание амплитудно-фазовой характеристики разомкнутой цени, построенной но частотной передаточной функции
причем размыкание системы производится по определенному правилу, которое дается ниже.
Как следствие, для устойчивости линейных систем первого и второго порядка с запаздыванием, оказывается, уже недостаточно только положительности .коэффициентов, а для систем третьего и более высокого порядка с запаздыванием неприменимы критерии устойчивости Вышнеградского, Рауса и Гурвица.
Ниже будет рассмотрено определение устойчивости только по критерию Найквиста, так как его использование для этой пели оказывается наиболее простым.
1Построение амплитудно-фазовой характеристики и исследование устойчивости но критерию Найквиста лучше всего производить, если передаточная функция разомкнутой системы представлена в виде (6.38). Для получения этого необходимо произвести соответствующим образом размыкание системы.
Для случая, изображенного на рис. 6.24, а, размыкание можно сделать в любом месте главной цепи, например так, как это показано. Тогда передаточная функция разомкнутой системы будет что совпадает по форме с (6.41).
Для случая, изображенного на рис. 6,24, б, размыкание главной цепи дает выражение
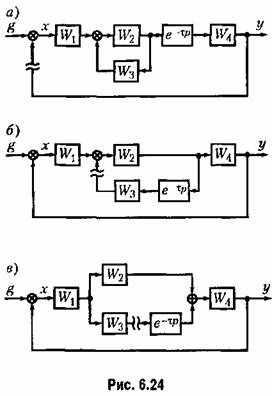
 функции разомкнутой системы, не удобное для дальнейших исследований: функции разомкнутой системы, не удобное для дальнейших исследований:
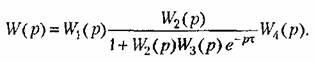
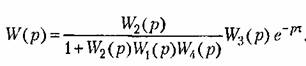
Наконец, в случае, изображенном на рис. 6.24, в, при размыкании системы в указанном месте получаем выражение, также совпадающее с (6.41):
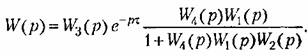
Частотную передаточную функцию (6.41) можно представить в виде
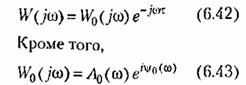
 Поэтому, представив выражение (6.41) в виде Поэтому, представив выражение (6.41) в виде

получаем значение модуля результирующей частотной передаточной функции

Таким образом, наличие звена с запаздыванием не меняет модуля и вносит только дополнительный фазовый сдвиг.
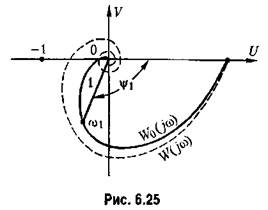
На рис. 6.25 изображена амплитудно-фазовая характеристика, соответствующая (6.43).

 введение постоянного запаздывания может улучшить условия устойчивости. введение постоянного запаздывания может улучшить условия устойчивости.
 при котором система оказывается на границе колебательной устойчивости. при котором система оказывается на границе колебательной устойчивости.
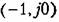 запишется следующим образом: запишется следующим образом:
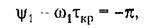
откуда критическое значение запаздывания

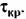
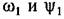 удобно делать при наличии построенных л. а. х. и л. ф. х. удобно делать при наличии построенных л. а. х. и л. ф. х.
Л. а. х. системы с запаздыванием совпадает с л. а. х. исходной системы (без запаздывания). Дополнительный фазовый сдвиг, который надо учесть при построении л. ф. х. системы с запаздыванием, определяемся (6.45).
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
В некоторых случаях могут использоваться аналитические расчеты. Так, например, рассмотрим статическую систему с одной постоянной времени. Частотная передаточная функция разомкнутой системы имеет вид

Приравняем модуль единице:
Отсюда находится частота, соответствующая


Фазовый сдвиг на этой частоте
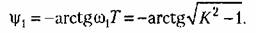
По формуле (6.46) находим критическое запаздывание:

По этому выражению на рис. 6.26 построена область устойчивости в координатах общий коэффициент усиления — относительное запаздывание.
|