Теория систем автоматического управленияИспользование вычислительных машин
За последнее время для исследования систем автоматического управления и, в частности, для построения переходных процессов стали широко применяться вычислительные машины непрерывного действия и цифровые вычислительные машины. Удобство первых заключается в том, что физическому процессу, протекающему в исследуемой системе, соответствует протекание в вычислительной машине (модели) некоторого другого аналогового процесса, описываемого теми же диффереициальными уравнениями, что и исходный процесс. Это позволяет изучать процессы в системах управления наиболее наглядно, так как каждый обобщенной координате в исследуемой системе соответствует некоторая переменная в вычислительной машине, например электрическое напряжение.
Моделирующие или аналоговые вычислительные машины позволяют моделировать как всю систему в целом, так и отдельные ее части. Так, например, часто вычислительная машина используется для моделирования объекта, например самолета, корабля, паровой турбины, двигателя внутреннего сгорания и т. п., а само управляющее устройство может быть реальным. При сопряжении реального управляющего устройства с объектом, в качестве которого выступает модель, получается замкнутая система, которая может быть исследована еще до того, как будет построен сам объект.
Вычислительные машины целесообразно использовать для исследования обыкновенных линейных систем в тех случаях, когда последние описываются дифференциальными уравнениями сравнительно высокого порядка и их аналитическое исследование становится малоэффективным. Однако наибольшее значение имеют вычислительные машины при исследовании линейных систем с переменными параметрами и нелинейных систем, поскольку для этих случаев пока еще мало разработано приемлемых для практики методов, а иногда аналитические методы вообще отсутствуют.
Точность моделирующих вычислительных машин обычно не превосходит нескольких процентов. В большинстве случаев этого оказывается достаточно для целей практики. Получение точности в десятые доли процента и выше связано со значительным увеличением стоимости машин. В этом отношении целесообразнее использовать цифровые вычислительные машины, которые сравнительно просто могут обеспечить высокую точность вычислений.
Следует заметить, что моделирование не призвано полностью заменить аналитические методы исследования систем. Комплекс технических задач, связанных с проектированием, конструированием, регулировкой и настройкой систем, весьма сложен, и он всегда должен опираться па сознательные расчетно-теоретические методы. Моделирование же процессов на вычислительных машинах во многом сводится к просматриванию некоторого количества возможных вариантов, разобраться в которых, а также наметить их предварительно можно при помощи существующих теоретических методов анализа и синтеза. Наилучшим решением в настоящее время является взаимная увязка расчетно-теоретических методов и методов моделирования, так как они взаимно дополняют друг друга и позволяют наиболее полно и быстро решить задачу разработки сложной системы управления.
Электронные модели. Электронные моделирующие вычислительные машины имеют наибольшее применение вследствие их сравнительной простоты в изготовлении и эксплуатации. Процессы в исследуемой системе изучаются при помощи наблюдения процессов в некоторой электронной схеме, которая описывается теми же дифференциальными уравнениями, что и исходная система.
Пусть исследуемая реальная система описывается совокупностью уравнений, разрешенных относительно первых производных
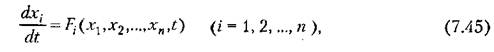
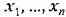 — переменные, описывающие повеление исследуемой системы. — переменные, описывающие повеление исследуемой системы.
В электронной модели должна быть реализована совокупность дифференциальных уравнений аналогичного вида:

 временем протекания процессов в модели т. временем протекания процессов в модели т.
 т. е. т. е.

При выборе масштаба времени должно учитываться то обстоятельство, что электронные модели могут точно работать при ограниченном времени протекания моделируемого процесса. Это время не должно обычно превышать нескольких сотен секунд, что связано с особенностями работы электронных интеграторов.
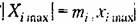 не превосходило предельного допустимого значения. не превосходило предельного допустимого значения.
Существует две разновидности электронных моделирующих машин: модели структурного типа и модели матричного типа. Первые позволяют моделировать структурную схему системы, что во многих случаях оказывается более удобным и наглядным.
Модели матричного типа требуют записи дифференциальных уравнений исследуемой системы в особой, матричной форме. Матричные модели менее удобны для исследования систем и потому используются реже.
Остановимся вначале па имеющих наибольшее применение моделях структурного типа. Они построены на базе так называемых операционных усилителей, выполняющих операции интегрирования, суммирования и умножения на постоянный множитель.
Операционный усилитель представляет собой усилитель постоянного тока с большим коэффициентом усиления по напряжению (десятки и сотни тысяч). Динамические свойства усилителя таковы, что он может быть замкнут 100%-ной отрицательной обратной связью через резистор или конденсатор без потери устойчивости (без генерации) в замкнутом состоянии.
Передаточная функция усилителя, замкнутого обратной связью (рис. 7.3) при большом коэффициенте усиления может быть достаточно точно представлена в виде
 ) )
 сопротивление в цепи обратной связи. сопротивление в цепи обратной связи.

Знак минус в формуле (7.47) показывает, что операционный усилитель инвертирует входной сигнал (меняет его знак). Современные усилители обычно имеют как инвертирующий, так и неинвертирующий входы.
Рассмотрим три основных режима работы усилителя.
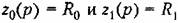 усилитель выполняет функцию умножения вход ной величины на постоянный множитель (рис. 7.4, а): усилитель выполняет функцию умножения вход ной величины на постоянный множитель (рис. 7.4, а):

Упрощенное изображение такого усилителя показано на рис. 7.4, а справа.
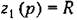 усилитель работает в режиме интегрирования входной величины (рис. 7.4, б) усилитель работает в режиме интегрирования входной величины (рис. 7.4, б)
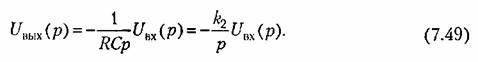
Два варианта упрощенного изображения такого усилителя изображены на рис. 7.4, б справа.
 что соответствует установке конденсатора во вход ной цени, усилитель работает в режиме дифференцирования (рис. 7.4, в): что соответствует установке конденсатора во вход ной цени, усилитель работает в режиме дифференцирования (рис. 7.4, в):

Упрощенное изображение такого усилителя показано на рис. 7.4, в справа. Режим дифференцирования обычно не используют при моделировании, так как в этом режиме сильно возрастает влияние высокочастотных помех и наводок.

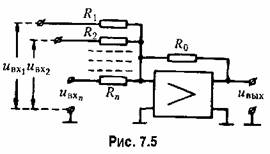 интегрирующий усилитель. интегрирующий усилитель.
В табл. 7.3 приведены типичные случаи использования операционного усилителя для получения различных динамических звеньев.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
В таблице использован машинный оператор дифференцирования


Электронная модель структурного типа имеет в своем составе несколько операционных усилителей, которые могут работать в режиме интегрирования, т. е. с конденсатором в цепи обратной связи. Число этих усилителей определяет наивысший
порядок дифференциального уравнения, которое может быть исследовано на данной модели. Кроме того, имеется ряд вспомогательных усилителей, при помощи которых можно осуществлять операции умножения на постоянный множитель (масштабирование), перемены знака (инвертирование) и суммирования.
Исследуемые процессы в виде изменения машинных переменных (напряжений) могут наблюдаться и фиксироваться при помощи осциллографов и графопостроителей.
Для приложения к электронной модели исследуемой системы задающих и возмущающих воздействий используются генераторы, которые могут воспроизводить требуемые функции времени, например линейную функцию, синусоиду, экспоненту, прямоугольную или треугольную волну и т. п., в виде соответствующего изменения электрического напряжения. Существуют также генераторы случайных величии.
Кроме того, электронная модель имеет ряд вспомогательных устройств, позволяющих после набора исследуемой задачи производить пуск и остановку решения дифференциальных уравнений, фиксацию решения в заданной точке, периодизацию решения и т. п.
Набор задачи на электронной модели структурного типа может быть осуществлен двумя способами:
по дифференциальному уравнению, которым описывается исследуемая система;
по структурной схеме исследуемой системы.
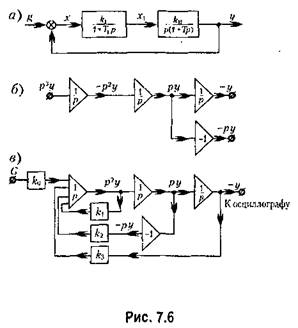
Рассмотрим порядок набора задачи на простейшем примере. Начнем с первого способа. Пусть дана система, структурная схема которой представлена на рис. 7.6, а. Для этой схемы передаточная функция разомкнутой системы

Дифференциальное уравнение замкнутой системы, записанное в символической форме, в соответствии с гл. 5 будет
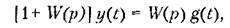
 задающее воздействие. задающее воздействие.
В рассматриваемом случае, учитывая (7.53), получим

 Учитывая соотношения Учитывая соотношения
 получим из (7.54) дифференциальное уравнение для машинных переменных: получим из (7.54) дифференциальное уравнение для машинных переменных:

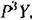 то на его выходе то на его выходе
 и на выходе третьего интегратора -- величина -Y. В результате можно реализовать дифференциальное уравнение (7,56), если на входе первого интегратора сложить с учетом знаков и масштабов все члены, входящие в правую часть формулы (7.56). Это показано на рис. 7.6. в. Значения коэффициентов делителей и на выходе третьего интегратора -- величина -Y. В результате можно реализовать дифференциальное уравнение (7,56), если на входе первого интегратора сложить с учетом знаков и масштабов все члены, входящие в правую часть формулы (7.56). Это показано на рис. 7.6. в. Значения коэффициентов делителей
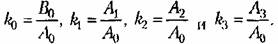
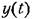 в реальной системе. в реальной системе.
Второй способ набора задачи на электронной модели заключается в том, что воспроизводится структурная схема, изображенная на рис, 7.6, а. Звено второго порядка удобнее представить в виде последовательно включенных звеньев первого порядка, каждое из которых может быть реализовано на базе одного интегратора. Это представлено на рис, 7.7, а. Схема набора, построенная в соответствии с табл. 7.3, изображена на рис. 7.7, б.

Для уяснения методики подсчета коэффициентов рассмотрим, например, второе звено (рис. 7.7). Исходная передаточная функция имеет вид
Это уравнение и набрано на втором интеграторе (рис. 7.7, б). Передаточные коэффициенты усилителя но соответствующим входам определяются из (7.59):

Аналогичным образом составляется схема набора остальных звеньев, входящих в структурную схему (рис. 7,7;а).
Получившаяся схема набора (рис. 7.7, б) представляет собой совокупность операционных усилителей в режиме интегрирования, замкнутых местными отрицательными обратными связями.
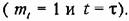
По сравнению с моделированием дифференциального уравнения (рис. 7.6) моделирование структурной схемы имеет преимущество в смысле большего соответствия модели исследуемой системе. Кроме того, моделирование структурной схемы позволяет просто учитывать при исследовании системы типичные нелинейности, например ограничение переменной величины, зону нечувствительности, релейную характеристику, люфт и т. н. Эти характеристики могут быть реализованы в электронной

модели посредством использования диодных элементов. В табл. 7.4 приведены некоторые типичные нелинейности и электронные схемы с диодными элементами, позволяющие реализовать в модели эти характеристики. Кроме этих простейших нелинейных блоков в электронных моделях применяются более сложные схемы, позволяющие реализовать различные криволинейные характеристики, операции возведения в степень и извлечения корня, операции перемножения двух переменных И Т. II.
На рис. 7.8 для иллюстрации приведена структурная

схема нелинейнойхледящей системы (рис. 7.8, а) и схема набора на электронной модели (рис. 7.8, б, Схема набора на рис. 7.8, б изображена несколько подробнее по сравнению со схемами на рис. 7.6 и 7.7.
Все, что было рассмотрено выше, относится к моделированию линейных-дифференциальных уравнений с постоянными коэффициентами. При необходимости исследовать процессы в системах с переменными коэффициентами или в системах с временным запаздыванием к линейной электронной модели добавляются соответственно блоки переменных коэффициентов и блоки временного запаздывания. Добавление нелинейных блоков позволяет исследовать процессы в нелинейных системах. Все эти добавочные блоки существенно повышают эффективность электронных моделей, так как позволяют сравнительно просто и достаточно точно исследовать процессы в сложных системах, что является в большинстве случаев недоступным для аналитических методов расчета.
Цифровые вычислительные машины
В вычислительных машинах непрерывного действия достижимая точность ограничивается точностью изготовления входящих в машину элементов. Повышение точности всегда связано со значительным удорожанием изготовления, а в некоторых случаях желаемая точность вообще не может быть достигнута при современном уровне техники. В цифровых вычислительных машинах принципиально может быть достигнута любая желаемая точность вычислений. Это связано лишь с увеличением числа используемых разрядов в изображении чисел, что вызывает умеренный рост стоимости вычислительных машин при росте их точности.
Цифровые вычислительные машины по своему принципу действия относятся к устройствам дискретного действия. Результаты вычислений выдаются этими машинами не непрерывно, а в виде последовательности дискретных чисел. Цифровые вычислительные машины могут применяться для различных целей. В том числе их можно использовать для решения линейных и нелинейных дифференциальных уравнений с постоянными и переменными коэффициентами, что нужно для исследования процессов в сложных системах управления.
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
Любые вычисления, которые производит цифровая вычислительная машина, сводятся к последовательности арифметических и логических операций. Это означает, что решение дифференциальных уравнений исследуемой системы осуществляется методами численного интегрирования по шагам и точность получаемого решения будет зависеть от величины выбранного шага интегрирования.
В настоящее время разработано большое количество разнообразных алгоритмических языков, которые значительно облегчают вопросы программирования, и множество стандартных программ для решения линейных и нелинейных дифференциальных уравнений. Современные оконечные устройства цифровых вычислительных машин позволяют получать решения как в виде таблиц, так и в виде готовых графиков.
К числу недостатков цифровых вычислительных машин следует отнести трудности сопряжения с реальной аппаратурой.
|