Теория систем автоматического управленияКорневые методы
Как было сказано выше, вид корней характеристического уравнения определяет характер переходных процессов в системе автоматического управления. Поэтому можно сформулировать требования но запасу устойчивости и быстродействию системы, не рассматривая самих переходных процессов, а накладывая определенные условия па корпи характеристического уравнения.
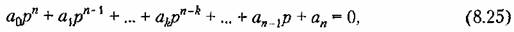 уравнение системы имеет вид уравнение системы имеет вид
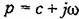 комплексное число. комплексное число.
Используя понятие среднегеометрического корпя
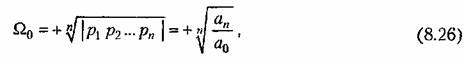
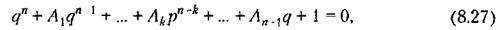
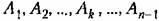 определяются выражением определяются выражением

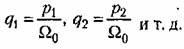
Исходное характеристическое уравнение (8.25) при возвращении к прежней комплексной величине получает вид
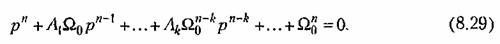
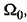 например, в 10 раз, то на основании теоремы подобия (табл. 7.2) переходный процесс, оставаясь подобным сам себе, будет протекать в 10 раз быстрее. например, в 10 раз, то на основании теоремы подобия (табл. 7.2) переходный процесс, оставаясь подобным сам себе, будет протекать в 10 раз быстрее.
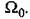
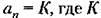 — коэффициент передачи разомкнутой системы. Следовательно, повышение быстродействия может осуществляться за счет увеличения коэффициента передачи К. Однако, как уже отмечалось, при этом уменьшается запас устойчивости замкнутой системы. В результате переходный процесс (рис. 8,3) становится более колебательным. — коэффициент передачи разомкнутой системы. Следовательно, повышение быстродействия может осуществляться за счет увеличения коэффициента передачи К. Однако, как уже отмечалось, при этом уменьшается запас устойчивости замкнутой системы. В результате переходный процесс (рис. 8,3) становится более колебательным.
Для оценки быстродействия системы может использоваться понятие степени устойчивости.
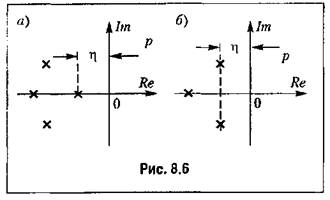
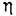 понимается абсолютное значение вещественной части ближайшего к мнимой оси корпя (рис. 8.6). Здесь могут быть два случая: когда ближайший корень является вещественным (рис. 8.6, а) и когда к мнимой оси ближе всего расположена пара комплексных корней (рис. 8.6, б). понимается абсолютное значение вещественной части ближайшего к мнимой оси корпя (рис. 8.6). Здесь могут быть два случая: когда ближайший корень является вещественным (рис. 8.6, а) и когда к мнимой оси ближе всего расположена пара комплексных корней (рис. 8.6, б).
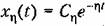
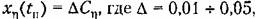 можно можно
получить приближенную зависимость между степенью устойчивости и временем переходного процесса:

Так, например, если принять Л = 0,05, то время переходного процесса составит
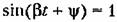 . Тогда получим выражение . Тогда получим выражение

Таким образом, и в этом случае величина степени устойчивости будет в какой-то мере определять быстроту затухания переходного процесса.
Более строго связь между видом переходного процесса и величиной степени устойчивости может быть определена для случая, когда исходное дифференциальное Уравнение системы имеет вид
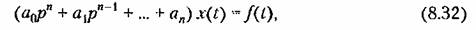
Тогда можно показать [АЛ], что при всех вещественных корнях или одной паре комплексных корней для переходной функции справедливо неравенство
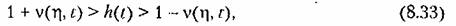
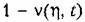 — —
функция, ограничивающая Н{1) снизу (миноранта).
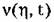 определяется из выражения определяется из выражения
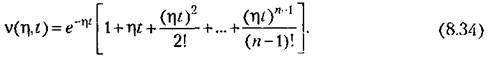
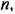 т. е. выглядит следующим образом: т. е. выглядит следующим образом:
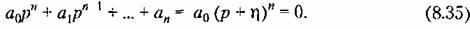
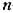 -кратный корень совпадает со среднегеометрическим корнем -кратный корень совпадает со среднегеометрическим корнем

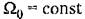 и всех вещественных корнях наименьшее время переходного процесса будет при всех кратных корнях, т. е. в случае (8.35). и всех вещественных корнях наименьшее время переходного процесса будет при всех кратных корнях, т. е. в случае (8.35).
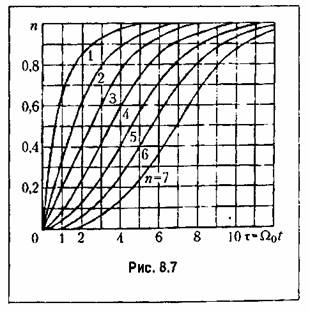
 для различных значений порядка дифференциального уравнения п. для различных значений порядка дифференциального уравнения п.
 получаем так называемое смещенное уравнение получаем так называемое смещенное уравнение
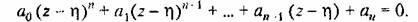
Раскрывая скобки и группируя подобные члены, получаем
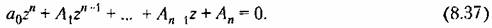
Это уравнение соответствует смещению осей на плоскости корней (рис. 8.6) влево па величину г|. В результате один (рис. 8.6, а) или Два (рис. 8.6, б) корпя попадают па мнимую ось, что соответствует границе устойчивости.
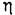 получается граница устойчивости. Напомним, что апериодической границе устойчивости соответствует равенство пулю свободного члена характеристического уравнения: получается граница устойчивости. Напомним, что апериодической границе устойчивости соответствует равенство пулю свободного члена характеристического уравнения:
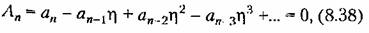
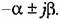 Эта склонность может характеризоваться отношением мнимой части корня (угловой частоты колебаний) к вещественной (коэффициенту затухания), которое называется колебательностью: Эта склонность может характеризоваться отношением мнимой части корня (угловой частоты колебаний) к вещественной (коэффициенту затухания), которое называется колебательностью:
 ) )
Колебательность связана с другим корневым показателем запаса устойчивости — с так называемым затуханием. Комплексные сопряженные корни дают в выражении для переходного процесса член вида
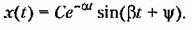
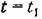 эта амплитуда равна эта амплитуда равна
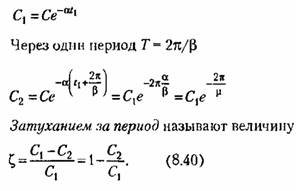
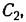 получаем получаем
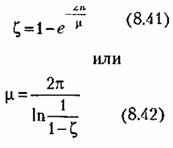
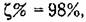 допустимая колебательность при этом составит допустимая колебательность при этом составит
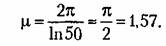
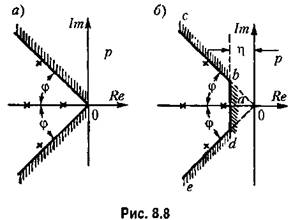
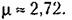
Задание определенной колебательности заставляет ограничивать область расположения корней двумя лучами (рис. 8.8, я), которые составляют с осью вещественных угол
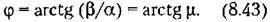
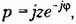 которая соответствует повороту координатных осей (рис. 8.8, б) против часовой стрелки на угол тс/2 - ф. При этом по крайней мере один корень попадает на мнимую ось и затем он отыскивается. Ввиду громоздкости этот метод почти не имеет практического значения. которая соответствует повороту координатных осей (рис. 8.8, б) против часовой стрелки на угол тс/2 - ф. При этом по крайней мере один корень попадает на мнимую ось и затем он отыскивается. Ввиду громоздкости этот метод почти не имеет практического значения.
При задании допустимых значений колебательности и степени устойчивости область расположения корней должна ограничиваться также вертикальной прямой, проходящей параллельно мнимой оси на расстоянии т (рис. 8.8, б). Расположению корней в этой области соответствует выдерживание требуемого запаса устойчивости, определяемого величиной колебательности и, или затуханием, и требуемой степени устойчивости Г|, характеризующей быстродействие системы.
Для определения параметров системы, при которых обеспечивается нахождение корней характеристического уравнения в заданной области, можно воспользоваться D-разбиением. В этом случае в плоскости двух параметров системы может быть построена область, аналогично построению области устойчивости (см. гл. 6).
Использование корней характеристического уравнения для оценки качества управления является не совсем полным, так как вид переходного процесса определяется не только левой, но и правой частью дифференциального уравнения. Л л я того чтобы учесть это обстоятельство, рассмотрим, например, зависимость между управляемой величиной и задающим воздействием, записанную посредством передаточной функции замкнутой системы (5.20):
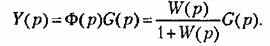
Передаточная функция замкнутой системы представляет собой дробнорациональную функцию
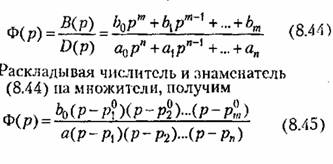
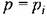 , передаточная функция обращается в бесконечность. , передаточная функция обращается в бесконечность.
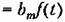 и формула (8.45) сводится к выражению и формула (8.45) сводится к выражению
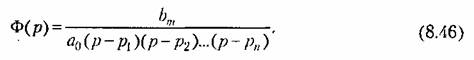
В этом случае вид переходного процесса определяется только расположением полюсов.
Задание области расположения полюсов и пулей позволяет более полно оценить вид переходного процесса. Не останавливаясь на подробном анализе, приведем без доказательства общие рекомендации, которых желательно придерживаться при выборе расположения полюсов и пулей передаточных функций [70].
1. Желательно располагать нули вблизи области расположения полюсов. Удаление пулей от области полюсов ведет к увеличению амплитуд собственных колебаний в переходном процессе.
2. Для уменьшения отклонений в переходном процессе часто бывает выгодно удалять полюсы друг от друга,
3. Приближение друг к другу не представляет опасности для тех полюсов, которые расположены далеко от мнимой оси.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
Кроме этих рекомендаций сохраняют свою силу ограничения на область расположения полюсов, накладываемые в связи с требованиями обеспечения определенного запаса устойчивости и быстродействия (см. рис. 8.8, б).
|