Теория систем автоматического управленияИнтегральные оценки
Интегральные оценки имеют целью дать общую оценку быстроты затухания и величины отклонения управляемой величины в совокупности, без определения того и другого в отдельности. Простейшей интегральной оценкой может служить величина

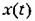 — отклонение управляемой величины от нового установившегося значения, которое она будет иметь после завершения переходного процесса. — отклонение управляемой величины от нового установившегося значения, которое она будет иметь после завершения переходного процесса.
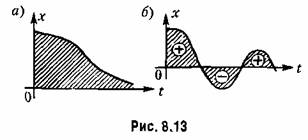
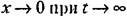 и этот интеграл имеет конечную величину Геометрически это будет площадь под кривой переходного процесса, построенного для отклонения (рис. 8.13, а). и этот интеграл имеет конечную величину Геометрически это будет площадь под кривой переходного процесса, построенного для отклонения (рис. 8.13, а).
Площадь будет тем меньше, чем быстрее затухает переходный процесс и чем меньше величина отклонения. Поэтому параметры системы рекомендуется выбирать таким образом, чтобы добиваться минимума этой интегральной оценки.
Для вычисления интеграла (8.53) нет
необходимости в нахождении х(t), так как его можно легко вычислить, используя изображение Лапласа или Хевисайда-Карсона. Действительно, изображение Лапласа определяется выражением
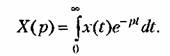
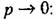
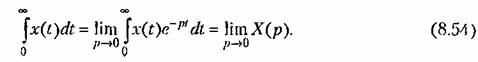
Неудобством интегральной оценки вида (8.53) является то, что она годится только
для монотонных процессов, когда не меняется знак отклонениях. Если же имеет место колебательный процесс (рис. 8.13, б), то при вычислении интеграла (8.53) площади будут складываться алгебраически и минимум этого интеграла может соответствовать колебаниям с малым затуханием или вообще без затухания. Так как форма переходного процесса при расчете систем управления может быть неизвестна, то применять интегральную оценку вида (8.53) оказывается практически нецелесообразным. Поэтому предлагалась другая интегральная оценка:

т. е. сумма абсолютных величин всех площадей под кривой переходного процесса. Но оказалось, что вычисление ее по коэффициентам уравнения затруднительно.
Квадратичная интегральная оценка. В свете вышесказанного целесообразно перейти к квадратичной интегральной оценке
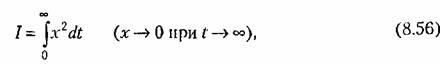
которая не зависит от знаков отклонений, а значит, и от формы переходного процесса (монотонной или колебательной).
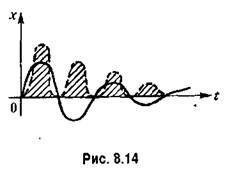
Величина / (8.56) будет тем меньше, чем меньше сумма заштрихованных на рис. 8.14 площадей (взятых для квадратов ординат), т. е. чем лучше переходный процесс приближается к идеальному скачку управляемой величины вслед за скачком задающего или возмущающего воздействия. Ниже будет показано, что такая оценка не всегда является лучшей, но пока остановимся на ней.
Заметим, что оценку (8.56) называют также квадратичной динамической ошибкой. Ее можно записать в безразмерном виде:
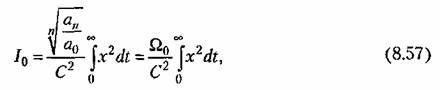
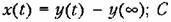 — некоторая величина, — некоторая величина,
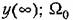 — среднегеометрическое значение корня характеристического уравнения (8.26). — среднегеометрическое значение корня характеристического уравнения (8.26).
Рассмотрим один из возможных способов вычисления квадратичной интегральной оценки (8.56) при скачкообразном внешнем воздействии.
В общем случае дифференциальное уравнение системы (в символической операторной записи) согласно (5.5) имеет вид
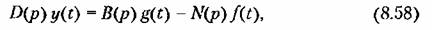
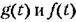 — задающее и возмущающее воздействия. — задающее и возмущающее воздействия.
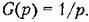 Перейдя в формуле (8.58) к изображениям, получаем Перейдя в формуле (8.58) к изображениям, получаем

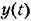 представляет собой дробно рациональную функцию: представляет собой дробно рациональную функцию:
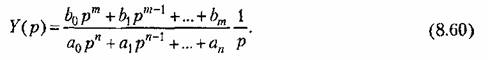
Отклонение х управляемой величины от нового установившегося состояния в переходном процессе, входящее в формулу (8.56), будет
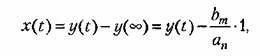
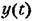 есть решение уравнения (8.59), а также оригинал изображения (8.60). есть решение уравнения (8.59), а также оригинал изображения (8.60).
Для изложенных условий при т < п ниже без вывода приводится формула [89], по которой может быть вычислена квадратичная интегральная оценка:
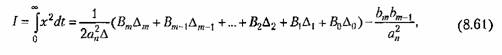
где Л есть следующий определитель п-го порядка (равный старшему определителю Гурвица, но записанный в несколько иной форме):

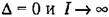
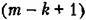 -го столбца столбцом -го столбца столбцом

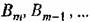 вычисляются по формулам: вычисляются по формулам:
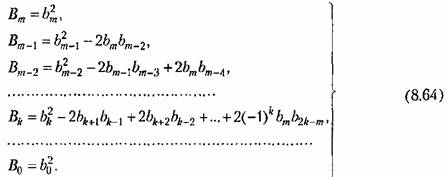
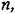 а в формулах (8,64) — с индексами меньше нуля и больше т. В том случае, когда т = п, формула (8.61) заменяется следующей: а в формулах (8,64) — с индексами меньше нуля и больше т. В том случае, когда т = п, формула (8.61) заменяется следующей:
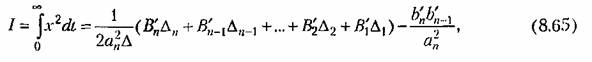

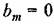 . Это обусловлено тем, что получение реакции системы па единичный импульс (весовой функции) эквивалентно дифференцированию переходной функции, получающейся при действии единичного скачка. В области изображений это эквивалентно умножению на комплексную величину р. . Это обусловлено тем, что получение реакции системы па единичный импульс (весовой функции) эквивалентно дифференцированию переходной функции, получающейся при действии единичного скачка. В области изображений это эквивалентно умножению на комплексную величину р.
В связи с этим квадратичную интегральную оценку при действии единичного импульса можно рассматривать в виде выражения
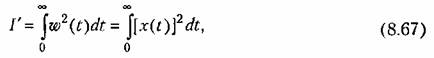
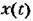 — отклонение управляемой величины от нового установившегося состояния в переходном процессе при действии единичной ступеньки задающего или возмущающего воздействия. — отклонение управляемой величины от нового установившегося состояния в переходном процессе при действии единичной ступеньки задающего или возмущающего воздействия.
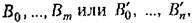 что обусловлено повышением степени т в выражении (8.60) на единицу при вычислении / по сравнению со случаем вычисления /. Интегральная оценка / также может использоваться в безразмерном виде аналогично формуле (8.57): что обусловлено повышением степени т в выражении (8.60) на единицу при вычислении / по сравнению со случаем вычисления /. Интегральная оценка / также может использоваться в безразмерном виде аналогично формуле (8.57):

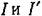 можно также производить на основании так называемой формулы Релея, которая будет доказана ниже, в главе 11. Здесь она будет приведена без доказательства. можно также производить на основании так называемой формулы Релея, которая будет доказана ниже, в главе 11. Здесь она будет приведена без доказательства.
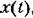 , то существует зависимость, определяемая теоремой Парсеваля , то существует зависимость, определяемая теоремой Парсеваля
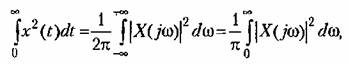
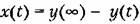 будет будет
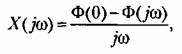
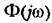 — частотная передаточная функция замкнутой системы. — частотная передаточная функция замкнутой системы.
Тогда
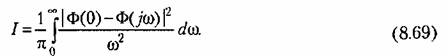
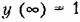 и Ф (0) = 1. Тогда формула (8.69) будет иметь вид и Ф (0) = 1. Тогда формула (8.69) будет иметь вид

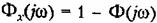 — частотная передаточная функция замкнутой системы по ошибке. — частотная передаточная функция замкнутой системы по ошибке.
Аналогичным образом для входного задающего воздействия типа единичного импульса 8(2), изображение которого равно 1, изображение Фурье исследуемого отклоненния
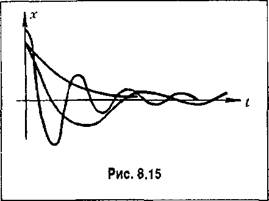
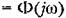 . В результате получаем . В результате получаем
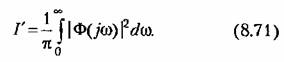
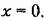
Это получается вследствие того, что оценка (8.56) учитывает только величину отклонения и быстроту затухания и никак не учитывает близость системы к колебательной границе устойчивости.
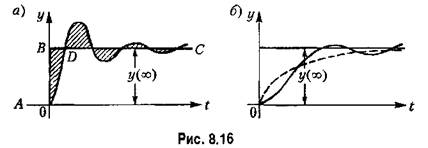
Если, например, подать на вход системы единичный скачок, то ошибка в переходном процессе определится заштрихованной частью на рис. 8.16, а. Очевидно, что величина интегральной оценки (8.56) будет тем меньше, чем ближе будет кривая переходного процесса к ломаной линии ЛОВС. Но приближение процесса к этой линии требует увеличения угла наклона кривой в начальной стадии процесса (приближение части кривой ОО к отрезку ОВ).
Увеличение же начальной скорости может вызвать значительное перерегулирование и, следовательно, малый запас устойчивости.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
Поэтому применяется еще другой вид интегральной оценки, в которой ограничение накладывается не только на величину отклонения х, но также и на скорость отклонения х. Эта улучшенная квадратичная интегральная оценка имеет вид

где Т — некоторая постоянная времени.
Выясним, какой вид переходного процесса будет получаться при выборе параметров системы по минимуму улучшенной интегральной оценки (8.72). Для этого проделаем следующие преобразования:
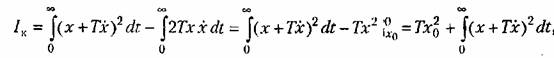
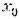 — начальное значение отклонения в переходном процессе. — начальное значение отклонения в переходном процессе.
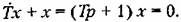 значение последнего выражения будет при выполнении условия значение последнего выражения будет при выполнении условия
Это есть дифференциальное уравнение первого порядка, решение которого имеет вид
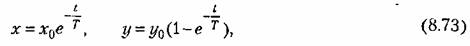
 — установившееся отклонение управляемой величины. — установившееся отклонение управляемой величины.
Этот процесс изображен па рис. 8.16 пунктиром. Следовательно, выбирая параметры системы но минимуму улучшенной интегральной оценки (8.72), можно приблизить переходный процесс к заданной экспоненте (8.73) с постоянной времени 7", которая носит в этом случае название экстремали. Из этих соображений можно заранее задаться определенной величиной Т.
Выбор параметров системы по улучшенной квадратичной интегральной оценке приводит к менее колебательным процессам по сравнению с использованием обычной квадратичной интегральной оценки (8.56).
Методика вычисления интеграла (8.72) сводится к тому, что правая его часть разбивается на два слагаемых:
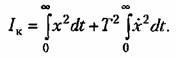
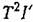 Поэтому для этого случая получаем Поэтому для этого случая получаем

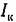 может также применяться в безразмерном виде аналогично (8.57) и (8.68): может также применяться в безразмерном виде аналогично (8.57) и (8.68):

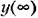
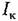 является их выражение через определители, которые трудно бывает раскрывать в буквенном виде при высокой степени характеристического уравнения. В этих случаях является их выражение через определители, которые трудно бывает раскрывать в буквенном виде при высокой степени характеристического уравнения. В этих случаях
можно использовать имеющиеся специальные приемы числовых расчетов. Сам определитель Л (8.62), как старший определитель Гурвица, согласно § 6.2 имеет вид
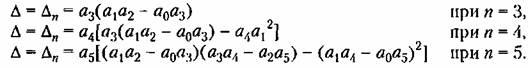
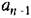 и и
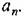 Все остальные определители оказываются проще. Все остальные определители оказываются проще.
Удобство интегральных оценок состоит в том, что они дают единый числовой критерий качества. Недостатком является то, что одному и тому же значению интегральной оценки могут отвечать разные формы переходного процесса, что создает недостаточную определенность решения задачи.
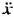 получим интегральную оценку в виде получим интегральную оценку в виде
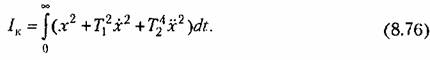
Эта оценка будет характеризовать приближение переходного процесса к экстремали, определяемой решением дифференциального уравнения
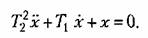
Экстремаль в данном случае будет соответствовать более сложной кривой, чем экспонента, что позволяет точнее задать желаемый вид переходного процесса. Однако нахождение интегральных оценок вида
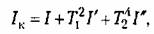
к которым сводится вычисление интеграла (8.76), сопряжено со значительными трудностями, что ограничивает их применение.
|