Теория систем автоматического управленияОпределение минимума интегральной оценки
Пусть требуется исходя из минимума какой-нибудь интегральной оценки, выбрать два каких-нибудь параметра а и р заданной автоматической системы. Указанные два параметра входят в коэффициенты дифференциального уравнения системы. Прежде всего по вышеприведенным формулам находится выражение соответствующей интегральной оценки. Это выражение, если все параметры системы заданы, кроме а и (3, имеет вид
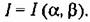
 вычисляем частные производные по а и р и приравниваем их пулю. В результате получаем два уравнения: вычисляем частные производные по а и р и приравниваем их пулю. В результате получаем два уравнения:
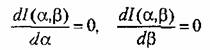
 с двумя неизвестными а м 0. Отсюда и определяются искомые значения параметров а и р. Чтобы убедиться в том, что это действительно минимум, а не максимум, можно вычислить значение /при полученных значениях а и (3, а затем при каких-нибудь соседних. Последние должны оказаться больше. Аналогично можно поступить и при выборе нескольких параметров по минимуму интегральной оценки. с двумя неизвестными а м 0. Отсюда и определяются искомые значения параметров а и р. Чтобы убедиться в том, что это действительно минимум, а не максимум, можно вычислить значение /при полученных значениях а и (3, а затем при каких-нибудь соседних. Последние должны оказаться больше. Аналогично можно поступить и при выборе нескольких параметров по минимуму интегральной оценки.
Функция (а, (3) не всегда обладает минимумом по рассматриваемым параметрам. Тогда нужно выбирать их по наименьшему значению интегральной оценки / внутри области, назначаемой из других соображении.
 (можно для наглядности построить график величины / в зависимости от выбираемого параметра). Аналогично нужно поступить и с другими выбираемыми параметрами системы. (можно для наглядности построить график величины / в зависимости от выбираемого параметра). Аналогично нужно поступить и с другими выбираемыми параметрами системы.
В конкретных расчетах всегда следует учитывать, что одновременно с таким выбором параметров нужно, во-первых, обеспечить хорошие статические свойства системы и, во-вторых, проследить, чтобы оптимальная точка не оказалась слишком близкой к границе устойчивости, так как всегда надо иметь некоторый запас устойчивости.
Рассмотрим в качестве примера дифференциальное уравнение третьего порядка
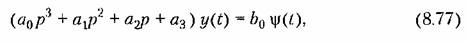
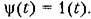 Тогда изображение по Лапласу управляемой величины будет Тогда изображение по Лапласу управляемой величины будет
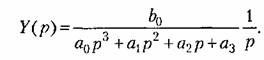
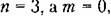 то в соответствии с формулой (8.61) имеем то в соответствии с формулой (8.61) имеем
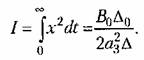
Далее но выражению (8.62) находим определитель
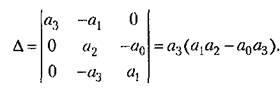
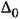 необходимо первый столбец определителя Д заменить на (8.63): необходимо первый столбец определителя Д заменить на (8.63):
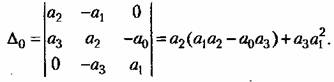
 • В результате получаем значение интегральной квадратичной оценки: • В результате получаем значение интегральной квадратичной оценки:
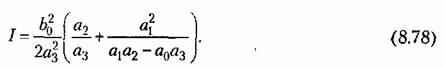
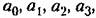 из условия минимума величины. из условия минимума величины.
Построим диаграмму квадратичной интегральной оценки па плоскости параметров Вышнеградского А и В. Согласно § 8.6
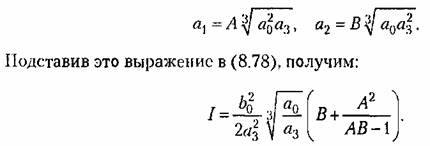
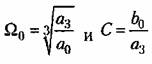 получаем получаем

 это дает на плоскости параметров Вышнегородского кривую это дает на плоскости параметров Вышнегородского кривую
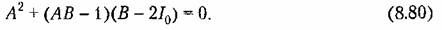
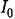 нанесены на диаграмме (рис. 8.17). Там же пунктиром нанесены кривые, взятые из диаграммы Вышнегородского (рис. 8.9), показывающие области колебательности (I) монотонного (II) и апериодического (III) процессов. Минимум интегральной оценки находим, приравнивая нулю частные производные: нанесены на диаграмме (рис. 8.17). Там же пунктиром нанесены кривые, взятые из диаграммы Вышнегородского (рис. 8.9), показывающие области колебательности (I) монотонного (II) и апериодического (III) процессов. Минимум интегральной оценки находим, приравнивая нулю частные производные:
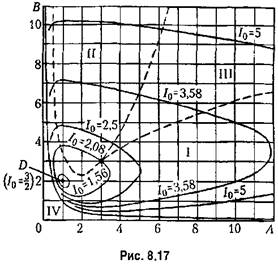
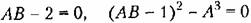
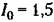 имеет место в точке О (рис. 8.17). Эта точка лежит, однако, слишком близко к границе устойчивости, что может не обеспечить необходимого запаса устойчивости (см., например, рис. 8.12). Практически лучше брать параметры системы не точно в точке D а несколько правее и выше. имеет место в точке О (рис. 8.17). Эта точка лежит, однако, слишком близко к границе устойчивости, что может не обеспечить необходимого запаса устойчивости (см., например, рис. 8.12). Практически лучше брать параметры системы не точно в точке D а несколько правее и выше.
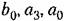 оста- оста-
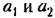 уравнения (8.77). уравнения (8.77).
|