Теория систем автоматического управленияТеория инвариантности и комбинированное управление
Одним из способов, позволяющих получить высокую точность в системах автоматического управления, является использование методов так называемой теории инвариантности [52]. Система является инвариантной по отношению к возмущающему воздействию, если после завершения переходного процесса, определяемого начальными условиями, управляемая величина и ошибка системы не зависят от этого воздействия. Система является инвариантной по отношению к задающему воздействию, если после завершения переходного процесса, определяемого начальными условиями, ошибка системы не зависят от этого воздействия.
Оба этих понятия имеют общую математическую трактовку. Рассмотрим эту трактовку для случая, когда на систему действует одно входное воздействие - задающее
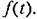 Пусть для ошибки системы имеет место дифференциальное уравнение Пусть для ошибки системы имеет место дифференциальное уравнение
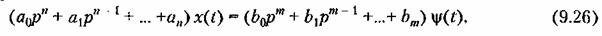

 Переходная составляющая определяется общим решением уравнения (9.26) без правой части, а вынужденная - частным решением уравнения (9.26) с правой частью. Переходная составляющая определяется общим решением уравнения (9.26) без правой части, а вынужденная - частным решением уравнения (9.26) с правой частью.
Изображение ошибки х(() при нулевых начальных условиях можно представить в следующем виде;
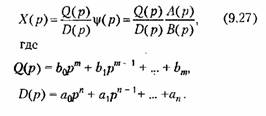
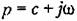

В соответствии с теоремой разложения (см. § 7.4) оригинал (9.27) в случае отсутствия кратных корней может быть представлен в виде

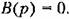
 будет тождественно равна нулю в следующих будет тождественно равна нулю в следующих
случаях.
 _ Этот случай является тривиальным, так как соответствует отсутствию входного воздействия, и он не представляет интереса, _ Этот случай является тривиальным, так как соответствует отсутствию входного воздействия, и он не представляет интереса,
 которое может быть любой функцией времени, т. е. меняться по произвольному закону. которое может быть любой функцией времени, т. е. меняться по произвольному закону.
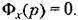 В иной записи В иной записи
 . Это условие приводит к тому, что следящая система должна иметь бес- . Это условие приводит к тому, что следящая система должна иметь бес-
 В реальных системах реализовать бесконечную полосу пропускания невозможно, поэтому реализация абсолютной инвариантности по задающему воздействию сталкивается с принципиальными трудностями. В реальных системах реализовать бесконечную полосу пропускания невозможно, поэтому реализация абсолютной инвариантности по задающему воздействию сталкивается с принципиальными трудностями.
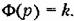 Однако это не меняет существа дела. Однако это не меняет существа дела.
 Здесь в принципе возможно получение абсолютной инвариантности поданному возмущению, однако в большинстве случаев приходится иметь дело со значительными техническими трудностями. Здесь в принципе возможно получение абсолютной инвариантности поданному возмущению, однако в большинстве случаев приходится иметь дело со значительными техническими трудностями.
 и и
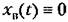
Этот случай соответствует частичной инвариантности. Система будет инвариантна к входным воздействиям определенного вида, например к воздействиям, которые могут быть представлены в виде степенной функции времени с положительными и ограниченными степенями, в виде суммы экспонент с заданными постоянными времени и т. п.
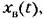 а приближенное равенство, мерой выполнения которого является некоторая величина е. Для оценки выполнения инвариантности до г существуют различные критерии, сливающиеся практически с критериями точности рассмотренными в главе 8. а приближенное равенство, мерой выполнения которого является некоторая величина е. Для оценки выполнения инвариантности до г существуют различные критерии, сливающиеся практически с критериями точности рассмотренными в главе 8.
Основным методом, используемым при построении инвариантных систем, является применение так называемого комбинированного управления.
Комбинированное управление. Под комбинированным управлением понимается такой метод построения замкнутых автоматических систем, когда, наряду с управлением но отклонению или ошибке, используется управление по задающему или возмущающему воздействию. Таким образом, в системе комбинированного управления осуществляется управление по замкнутому и разомкнутому циклам.
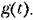 Структурная схема такой системы изображена на рис, 9.10, а. Структурная схема такой системы изображена на рис, 9.10, а.
 управляемая величина у связана с задающим воздействием через пере управляемая величина у связана с задающим воздействием через пере
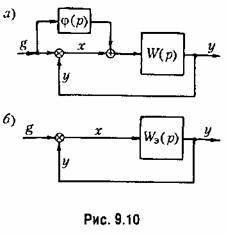
даточную функцию замкнутой системы;

 — передаточная функция разомкнутой системы. — передаточная функция разомкнутой системы.
При введении управления по задающему воздействию управляемая величина определяется выражением

Эквивалентная передаточная функция замкнутой системы с учетом управления по задающему воздействию

Из последнего выражения видно, в частности, что введение управления по задающему воздействию не меняет характеристического уравнения системы, работающей по отклонению, так как знаменатель передаточной функции замкнутой системы одинаков в (9.30) и (9.32). Это обстоятельство является замечательным свойством систем комбинированного управления.
Введение дополнительного управления по задающему воздействию не меняет левой части дифференциального уравнения. Это означает, что не будут нарушаться не только условия устойчивости, но сохранятся оценки качества переходного процесса, базирующиеся на использовании корней характеристического уравнения.
Из выражения (9.32) по известным соотношениям (5.19) и (5.26) могут быть пайлены эквивалентная (т. е. с учетом управления по задающему воздействию) передаточная функция по ошибке
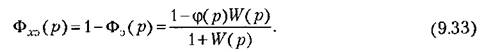
и передаточная функция разомкнутой системы

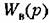 позволяет заменить структурную схему системы комбинированного управления эквивалентной ей обычной схемой системы, работающей по отклонению (рис. 9.10, б). позволяет заменить структурную схему системы комбинированного управления эквивалентной ей обычной схемой системы, работающей по отклонению (рис. 9.10, б).
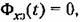 получаем получаем

Разложив последнее выражение в ряд но возрастающим степеням оператора р, получим необходимый вид функции, определяющей вводимый сигнал от управляющего воздействия:
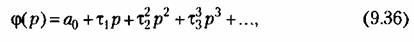
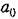 — безразмерное число. — безразмерное число.
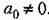
Таким образом, при введении управления но задающему воздействию для получения полной инвариантности необходимо вводить первую и высшие производные от задающего воздействия.
Обычно точно можно ввести только в некоторых случаях первую производную. а все последующие производные могут быть получены приближенно при помощи использования известных дифференцирующих звеньев (см., например, рис. 4.23 и 4.24). Поэтому практически может быть получена не полная, а частичная инвариантность. Это соответствует введению ограниченного числа первых членов разложения (9.36).

Так, например, введением первой производной от задающего воздействия в системе с астатизмом первого порядка можно получить равной нулю скоростную ошибку, т. е. повысить степень астатизма относительно задающего воздействия на единицу. Вводя первую и вторую производные (даже приближенно), можно повысить степень астатизма на два и т. д. Это дает обращение в нуль соответствующих коэффициентов ошибки (8.20).
В некоторых случаях сигнал по задающему воздействию может вводиться не непосредственно на вход системы, как это показано на рис. 9.10, а в некоторую точку внутри канала управления (рис. 9.11).
В этом более общем случае эквивалентная передаточная функция замкнутой системы будет иметь вид

Эквивалентная передаточная функция по ошибке

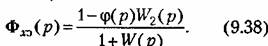
Эквивалентная передаточная функция разомкнутой системы

Условие полной инвариантности

В качестве примера рассмотрим следящую систему (см. рис. 6.4) при введении управления по первой производной от угла поворота командной оси, которое осуществляется при помощи тахогеиератора. Электромеханическая и структурная схемы для этого случая изображены на рис. 9.12.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
В соответствии с общим случаем, изображенным на рис. 9.11, имеем:

Эквивалентная передаточная функция замкнутой системы (9.37)
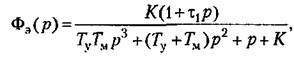
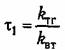 — постоянная времени цепи первой производной от угла поворота командной оси. — постоянная времени цепи первой производной от угла поворота командной оси.
Эквивалентная передаточная функция по ошибке (9.38)

Скоростная ошибка будет равна нулю в том случае, когда в числителе последнего выражения будет равен нулю коэффициент при операторе в первой степени. Отсюда получаем условие частичной инвариантности (ликвидация скоростной ошибки):

Из (9.39) можно найти эквивалентную передаточную функцию разомкнутой системы:
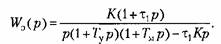
При выполнении условия (9.41) эквивалентная передаточная функция разомкнутой системы будет соответствовать астатизму второго порядка:
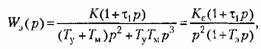
 — эквивалентная — эквивалентная

постоянная времени.
В качестве второго примера рассмотрим инерциальную вертикаль (рис. 9.13, а). Принцип работы ее заключается в том, что акселерометр А воспринимает ускорение перемещения подвижного объекта, на котором установлена стабилизированная платформа (СП), и составляющую ускорения силы тяжести, возникающую при наклоне этой платформы на некоторый угол а (ошибка вертикали). Таким образом, акселерометр определяет ускорение
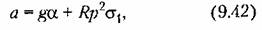
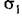 — путь, пройденный объектом по Земле, в дуговых единицах. — путь, пройденный объектом по Земле, в дуговых единицах.
Это ускорение дважды интегрируется и поступает на стабилизированную платформу, которая поворачивается на угол

 — коэффициенты передачи первого и второго интеграторов. — коэффициенты передачи первого и второго интеграторов.
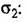

Для рассмотренных уравнений (9.42)~(9.44) инерциальной вертикали изобразим структурную схему (рис. 9.13, б). Сравнивая ее с рис. 9.11, можем записать:

Условие полной инвариантности (9.40)
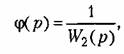
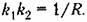 Тогда передаточная функция разомкнутой системы Тогда передаточная функция разомкнутой системы

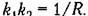
Заметим, что в рассмотренном случае особенно важно иметь нулевые начальные условия вследствие того, что передаточной функции (9.48) соответствует характеристическое уравнение
 ) )
 Оно имеет чисто мнимые корни Оно имеет чисто мнимые корни

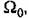 что будет нарушать работу вертикали. что будет нарушать работу вертикали.
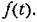 Передаточная функция по возмущению здесь будет иметь вид Передаточная функция по возмущению здесь будет иметь вид
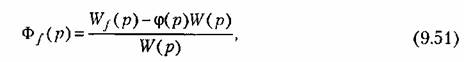
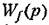 — передаточная функция поданному возмущению в разомкнутой системе, — передаточная функция поданному возмущению в разомкнутой системе,
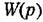 — передаточная функция разомкнутой системы. — передаточная функция разомкнутой системы.


Эта функция также может быть представлена в виде ряда аналогично формуле (9.36):


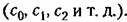
В заключение заметим, что возможно использование комбинированных систем с введением управления по нескольким возмущающим воздействиям и получением полной или частичной инвариантности

по каждому из них. Однако это приводит, конечно, к усложнению схемы.
|