Теория систем автоматического управленияДемпфирование с подавлением средних частот
Выведение амплитуднофазовой характеристики из запретной зоны (рис. 10.17) может быть произведено при помощи подавления усиления в области частот, соответствующей части характеристики между точками а и Ь. В результате будет получена характеристика, изображенная на рис. 10.17 пунктиром.
Подавление средних частот может быть осуществлено включением в цепь управления последовательного интегродифферепцирующего звена (табл. 10.1), имеющего л. а. х., изображенную там же. Из вида л. а. х. вытекает, что звено подавляет усиление в некоторой области средних частот. Вместо пассивного интегро-диф-ференцирующего звена могут применяться его эквиваленты, например гибкая отрицательная обратная связь, охватывающая инерционный усилитель (табл. 10.4).
По своим свойствам демпфирование с подавлением средних частот занимает промежуточное положение между двумя рассмотренными методами. При демпфировании с подавлением средних частот сохраняется быстродействие системы и сохраняется полоса пропускания. Этот вид демпфирования является наиболее распространенным.
Демпфирование с введением отрицательных фазовых сдвигов. Сущность этого метода можно уяснить, например, из рассмотрения рис. 6.22. На рис. 6.22, б изображен случай, когда из-за наличия в канале разомкнутой системы консервативного звена, имеющего чисто мнимые полюсы, замкнутая система будет неустойчивой. Добавление отрицательного фазового сдвига вызовет закручивание а. ф. х. по часовой стрелке. В результате система в замкнутом состоянии может быть сделана устойчивой (рис. 6.22, а).
 подобные звенья оказываются обычно неминимально-фазовыми, то такой метод демпфирования иногда называют в литературе методом демпфирования с использованием неминимально-фазовых звеньев. подобные звенья оказываются обычно неминимально-фазовыми, то такой метод демпфирования иногда называют в литературе методом демпфирования с использованием неминимально-фазовых звеньев.
Демпфирование с введением отрицательных фазовых сдвигов оказывается эффективным в случае наличия в канале разомкнутой системы консервативных, а также колебательных звеньев со слабым демпфированием. В нервом случае это приводит к появлению в амплитудной частотной характеристике (или в л. а. х.) резонанс-пых пиков бесконечной высоты, а но втором — к резонансным пикам конечной, но значительной высоты. Использование демпфирования других типов здесь оказывается затруднительным.
 . В результате сохраняется быстродействие демпфируемой системы и сохраняется ее полоса пропускания. . В результате сохраняется быстродействие демпфируемой системы и сохраняется ее полоса пропускания.
Рассмотренные иыше методы демпфирования являются основными, по лишь иллюстрируют те идеи, которые используются при повышении запаса устойчивости. В практике, в зависимости от конкретных условий, могут использоваться и более сложные изменения динамических свойств системы управления. Так, например, может осуществляться подавление средних частот с одновременным поднятием высоких, поднятие высоких частот с подавлением их некоторой области (фильтрация определенных частот) и т. п.
Примеры
1, Система управления движущимся объектом. Рассмотрим систему управления, изображенную на рис. 10.18. Здесь обозначено: ГН — гироскоп направления, измеряющий отклонение движущегося объекта от заданного курса; П — потенциометр; Д — двигатель рулевого устройства и Р — редуктор. При отклонении объекта от заданного курса на угол а движок потенциометра отклоняется на тот же угол. В результате па усилитель поступает напряжение. Пройдя усилитель, это напряжение поступает на двигатель и руль объекта начинает поворачиваться.
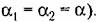
Передаточная функция разомкнутой системы


Найдем передаточные функции отдельных звеньев.
Потенциометр. Считая потенциометр безынерционным звеном получаем

 — крутизна потенциометра [В/рад]. — крутизна потенциометра [В/рад].
У с и л и т е л ь. При безынерционном усилителе

 — коэффициент усиления но напряжению. — коэффициент усиления но напряжению.
Двигатель совместно с редуктором. Передаточная функция двигателя с редуктором в случае пренебрежения переходными процессами в обмотке управления имеет вид

 — электромеханическая постоянная времени. — электромеханическая постоянная времени.
Объект. Будем считать, что угловая скорость поворота объекта по курсу пропорциональна углу отклонения руля. Тогда угол поворота будет пропорционален интегралу от угла поворота руля по времени.
При учете инерционности объекта его передаточная функция имеет вид

 — постоянная времени объекта. — постоянная времени объекта.
Передаточная функция разомкнутой системы

 —коэффициент передачи разомкнутой системы. —коэффициент передачи разомкнутой системы.
Найдем характеристическое уравнение системы

Достаточно одного взгляда па это уравнение, чтобы убедиться в неустойчивости
системы при любом коэффициенте передачи К. Это вытекает из того, что в характеристическом уравнении отсутствует член с оператором в первой степени. Такая

неустойчивость называется структурной неустойчивостью, так как при дайной структуре изменение параметров схемы любым образом не дает устойчивости.
На рис. 10.19 изображена амплитудно-фазовая характеристика, соответствующая передаточной функции разомкнутой системы (10.51). Из вида характеристики
 и замкнутая система окажется устойчивой. Для введения положительного фазового сдвига необходимо применить демпфирование с поднятием высоких частот, что достигается включением звеньев дифференцирующего типа. и замкнутая система окажется устойчивой. Для введения положительного фазового сдвига необходимо применить демпфирование с поднятием высоких частот, что достигается включением звеньев дифференцирующего типа.
 можно считать пропорциональным угловой скорости а поворота ДУС. В результате вместо (10.41) будем иметь можно считать пропорциональным угловой скорости а поворота ДУС. В результате вместо (10.41) будем иметь


Передаточная функция разомкнутой системы
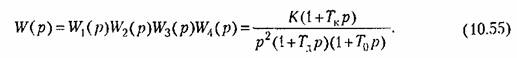
Характеристическое уравнение системы (10.72) в этом случае уже не имеет пропуска членов;
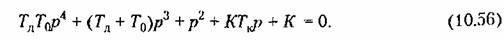
 и коэффициента передачи К может быть получена устойчивая система. и коэффициента передачи К может быть получена устойчивая система.
2. Следящая система. Схема следящей системы без корректирующих средств изображена на рис. 6.4. В этом случае предельная добротность по скорости из условия устойчивости определяется неравенством, полученным в § 6.2:

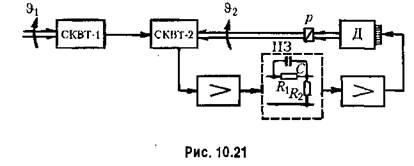
Рассмотрим случай демпфирования с поднятием верхних частот. Включим последовательно в канал усиления (рис. 10.21) пассивное дифференцирующее звено ПЗ с передаточной функцией

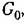 вносимое звеном на низких частотах компенсируется соответствующим увеличением коэффициента усиления усилителя. Тогда передаточная функция разомкнутой системы, полученная в § 6.2, вносимое звеном на низких частотах компенсируется соответствующим увеличением коэффициента усиления усилителя. Тогда передаточная функция разомкнутой системы, полученная в § 6.2,
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение

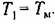 Тогда вместо (10.58) получим Тогда вместо (10.58) получим


Найдем характеристическое уравнение
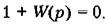
Подстановка выражения для передаточной функции (10.59) приводит к уравнению
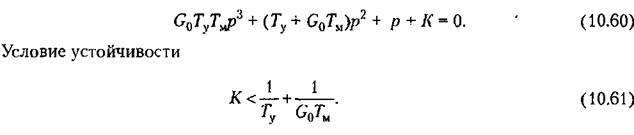
 можно получить устойчивость при любом значении добротности следящей системы. можно получить устойчивость при любом значении добротности следящей системы.
Рассмотрим теперь случай демпфирования с подавлением средних частот той же следящей системы. Для этой цели охватим часть усилителя, содержащую инерционность, гибкой отрицательной обратной связью (рис. 10.22, а). Согласно табл. 10.4 это эквивалентно включению последовательного иптегро-дифференцирующего звена, обладающего свойством подавлять средние частоты.
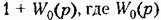 представляет собой передаточную функцию по петле обратной местной связи представляет собой передаточную функцию по петле обратной местной связи

 — постоянная времени дифференцирующего конденсатора в цепи обратной связи. — постоянная времени дифференцирующего конденсатора в цепи обратной связи.
В результате получим

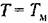 . Это всегда легко сделать выбором параметров Я. и С. Тогда . Это всегда легко сделать выбором параметров Я. и С. Тогда


Вместо включения гибкой отрицательной обратной связи аналогичный эффект может быть достигнут введением в прямую цепь эквивалентного пассивного интегро-дифференцирующего звена (рис. 10,22, б).
|