Теория систем автоматического управленияСлучайные процессы в системах автоматического управления
Вводные замечания
До сих пор поведение систем автоматического управления исследовалось при определенных, заданных во времени задающих и возмущающих воздействиях (ступенчатая функция, импульсная функция, гармоническое воздействие и т. д.)
Однако во многих случаях характер воздействия бывает таким, что его нельзя считать определенной функцией времени. Оно может принимать с течением времени самые разнообразные случайные значения. В таких случаях мы можем оценить только вероятность появления той или иной формы воздействия в тот или иной момент времени. Это происходит не потому, что оно неизвестно заранее, а потому, что сама природа реального задающего или возмущающего воздействия такова, что величина его в каждый момент времени и процесс его изменения с течением времени зависят от множества разнообразных величин, которые случайным образом могут комбинироваться друг с другом, появляться одновременно или с любым сдвигом во времени и т. д.
Возьмем, например, систему автоматической стабилизации напряжения электрического генератора. Возмущающее воздействие здесь является результатом изменения нагрузки в сети, зависящей от включения, выключения и изменения режима работы множества потребителей электрической энергии.
Другой пример — автопилот. На него действуют обычно возмущающие воздействия случайного характера: порывы ветра и изменения других атмосферных факторов, изменение тяги, изменения напряжения питания усилителей и рулевых машинок и т. д.
Третий пример — следящие системы, на вход которых попадают вместе с полезным сигналом помехи. Например, в радиолокационной системе сопровождения отраженный от цели сигнал содержит в себе помехи в виде многочисленных флуктуации, происходящих от вибраций и поворотов цели, замирания сигнала и т. п.
Аналогичные помехи случайной природы имеют место в других автоматических устройствах.
В следящих системах не только возмущающие воздействия и помехи являются случайными, но и сам полезный сигнал, который должен воспроизводиться (задающее воздействие), как правило, носит случайный характер.
Прежде чем рассматривать поведение автоматических систем при случайных воздействиях, напомним некоторые сведения о случайных величинах, случайных процессах и об их вероятностных характеристиках.
К категории случайных событий можно отнести такие, точное предсказание протекания которых в каждом отдельном случае оказывается невозможным.
 Относи- Относи-
 называется частотой события выпадения герба, а величина называется частотой события выпадения герба, а величина
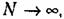 то частоты событий будут стремиться к некоторому пределу то частоты событий будут стремиться к некоторому пределу

называемому вероятностью данного события. В рассмотренном случае очевидно, что
обе вероятности выпадения герба и цифры одинаковы и равны 0,5.
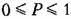
Если событие является невозможным, вероятность его равна пулю; если событие является достоверным, его вероятность равна единице.

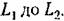
Вероятностные характеристики дискретных случайных величин. Чтобы полностью знать дискретную случайную величину, надо иметь следующие данные:
а) все возможные значения, которые она может принимать при данных услови ях задачи или опыта;
б) вероятность появления каждого из этих значений.
 и вероятность каждого значения будет соответственно и вероятность каждого значения будет соответственно
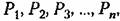 то можно представить так называемый закон распределения случайной величины в виде таблицы 11.1. то можно представить так называемый закон распределения случайной величины в виде таблицы 11.1.
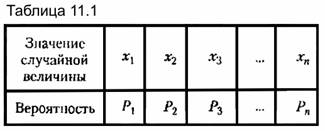
При этом должно выполняться условие

Пусть, например, производится опыт бросания игральной кости. Очевидно, что при каждом бросании число выпавших очков, которое представляет собой случайную величину, может принимать одно из следующих значений: 1, 2, 3, 4, 5, 6. Если кость совершенно симметрична, то вероятность выпадения каждой из этих цифр является одинаковой. Так как число различных значений, которое может принимать случайная величина, равно шести, то из (11.2) имеем
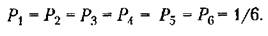
Графически этот закон распределения изображен на рис. 11.2. Он представляет собой равновероятное распределение в некотором интервале (в рассматриваемом случае от 1 до 6).
В некоторых случаях закон распределения случайной величины может задаваться в аналитической форме.
 Примерами таких величин могут служить число пассажиров вагона трамвая, число вызовов на телефонной станции в течение какого-либо определенного отрезка времени и т. н. Этот закон для целых значений числах записывается следующим образом: Примерами таких величин могут служить число пассажиров вагона трамвая, число вызовов на телефонной станции в течение какого-либо определенного отрезка времени и т. н. Этот закон для целых значений числах записывается следующим образом:

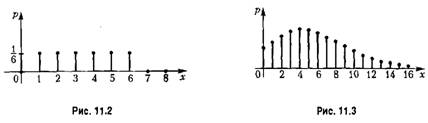
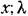 представляет собой среднее значение данной дискретной величины, полученное но результатам большого числа опытов. Графически этот закон имеет вид, изображенный на рис. 11.3, причем место максимума зависит от величины X. представляет собой среднее значение данной дискретной величины, полученное но результатам большого числа опытов. Графически этот закон имеет вид, изображенный на рис. 11.3, причем место максимума зависит от величины X.
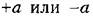 (рис. 11.4). (рис. 11.4).

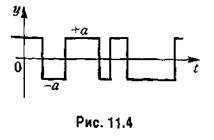
 и т. д. и т. д.
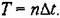 Тогда вероятность отсутствия перемены знака на этом интервале можно найти из выражения Тогда вероятность отсутствия перемены знака на этом интервале можно найти из выражения
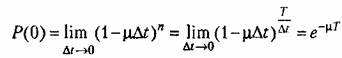
Аналогичным образом можно показать, что вероятность одной перемены знака

и т.д. Следовательно, вероятность х перемен знака на интервале времени Г будет определяться выражением

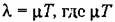 — среднее — среднее
число перемен знака на интервале времени Г, которое будет наблюдаться при многократном повторении наблюдения.
Хотя закон распределения полностью определяет случайную величину для практики нужны некоторые более простые осредненные характеристики случайной величины, выражающиеся в виде обыкновенных неслучайных чисел.
Одной из таких характеристик является среднее значение, или математическое ожидание, случайной величины. Оно определяется из выражения

Так, например, для случая бросания игральной кости
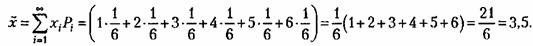
Вообще для равновероятного закона распределения (11.5) превращается в формулу

Для случайной величины, распределенной по закону Пуассона, среднее значение, подсчитанное по формуле (11.5), дает
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
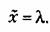
Основные свойства среднего значения случайной величины следующие. 1. Для любых случайных величин среднее значение их суммы равно сумме средних значений этих величин:

2. Среднее значение произведения случайных величин, независимых друг от друга, равно произведению средних значений этих величин:
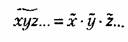
Последняя формула не распространяется на общий случай любых случайных величин.
В виде обобщения понятия среднего значения (11.5) отметим, что выражение

называется моментом т-го порядка случайной величины х. В частности, момент нулевого порядка выражает свойство (11.2), и он всегда равен единице:
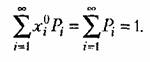
Момент первого порядка есть среднее значение (математическое ожидание) случайной величины (11.5). Момент второго порядка

есть средний квадрат случайной величины.
Часто используется так называемое среднеквадратичное значение случайной величины, представляющее собой корень квадратный из среднего квадрата случайной величины:

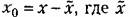 — среднее значение. Тогда аналогично формуле (11,6) можно ввести понятие центрального момента т-го порядка — среднее значение. Тогда аналогично формуле (11,6) можно ввести понятие центрального момента т-го порядка

Из формулы (11.7) следует, что центральный момент первого порядка всегда равен нулю.
Обратимся теперь к характеристикам рассеяния дискретной случайной величины.
 есть отклонение случайной величины от ее среднего значения. Это отклонение является случайной величиной, как и сама величинах. есть отклонение случайной величины от ее среднего значения. Это отклонение является случайной величиной, как и сама величинах.
Средним отклонением А называется среднее значение (математическое ожидание) абсолютной величины отклонения, т. е.

Заметим, что без знака абсолютного значения было бы
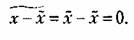
Для рассмотренного выше примера бросания игральной кости
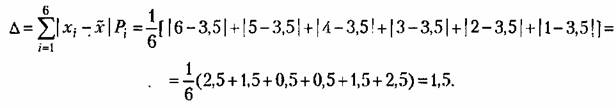
Среднее отклонение случайной величины является уже не случайной величиной, а обычным числом.
Дисперсией называется средний квадрат отклонения случайной величины от ее среднего значения. Она совпадает с центральным моментом второго порядка:

Дисперсия может быть легко вычислена на основании свойства среднего значения:

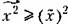 , то дисперсия может , то дисперсия может

Корень квадратный из дисперсии называется среднеквадратичным отклонением случайной величины от среднего значения:

Для рассмотренного выше примера бросания игральной кости
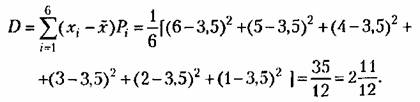
Среднеквадратичное отклонение

Укажем простейшие свойства среднеквадратичных отклонений.
1. При сложении независимых случайных величин
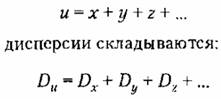
Поэтому среднеквадратичное отклонение суммы независимых случайных величин

Эта формула часто применяется в измерительной технике и в автоматике для вычисления среднеквадратичных ошибок.
2. Пусть имеется п случайных величин

с одинаковыми средними значениями тис одинаковыми законами распределения. Тогда их среднее арифметическое
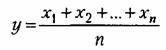
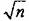 раз меньше, чем для каждой из составляющих (в случае независимых случайных величин): раз меньше, чем для каждой из составляющих (в случае независимых случайных величин):

Например, если производится п измерений одной и той же физической величины, то их среднее арифметическое хотя тоже является случайной величиной, но всегда надежнее (имеет меньшее среднеквадратичное отклонение), чем каждое измерение в отдельности. Здесь случайные ошибки измерения в известной мере компенсируются. Но надо помнить, что систематические ошибки приборов при этом остаются в полной мере в составе среднего арифметического и никакой массовостью измерений скомпенсированы быть не могут.
 (с вероятностью, как угодно близкой к единице). (с вероятностью, как угодно близкой к единице).
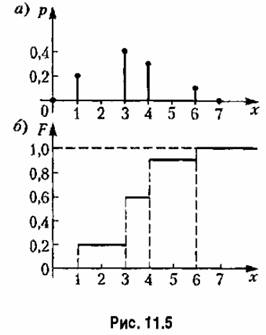
Замечание в скобках означает, что это практически достоверно, по не абсолютно, потому что среднее арифметическое есть все же случайная величина. Таким образом, при большом п и указанных условиях

Этот закон больших чисел, доказанный П. Л. Чебышевым, имеет первостепенное значение для обработки экспериментальных данных и для учетной статистики.
Введем теперь понятие интегрального за кона распределения. Интегральным законом распределения или функцией распределения называется вероятность того, что случайная величина примет значение, меньшее некоторого значения х. Математически эта формулировка записывается в виде

 — текущее значение случайной величины х. — текущее значение случайной величины х.

Например, для закона Пуассона (11.3), когда дискретная случайная величина может принимать значения х = 0, 1, 2, 3,..., функция распределения

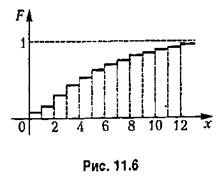
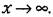
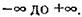 Следовательно, функция распределения (интегральный закон распределения) для непрерывной случайной величины будет изображаться непрерывной кривой. На рис. 11.7 показа ны оба упомянутых выше варианта. Вероятность Следовательно, функция распределения (интегральный закон распределения) для непрерывной случайной величины будет изображаться непрерывной кривой. На рис. 11.7 показа ны оба упомянутых выше варианта. Вероятность
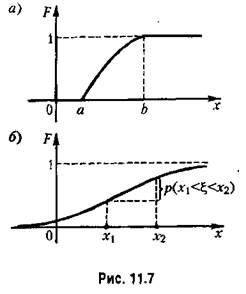
того, что непрерывная случайная величина примет
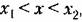 будет иметь конечное значение, а именно: будет иметь конечное значение, а именно:

Вероятность того, что непрерывная случайная величина содержится в промежутке между х и
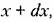 будет будет

называется плотностью вероятности.
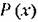

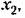 определяется формулой определяется формулой
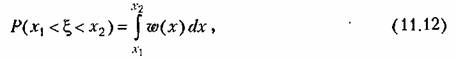
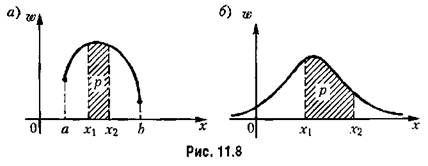
что геометрически выражается заштрихованной площадью на рис. 11.8. Кроме того, имеет место зависимость

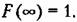
Формула (11.14) соответствует моменту нулевого порядка. Среднее значение (математическое ожидание) соответствует моменту первого порядка:

что вытекает из формулы (11.5) как предел суммы.
Моменты высших порядков по аналогии с (11.6) будут $

Таким же образом можно вычислить центральный момент тп-го порядка

Как и в случае дискретных случайных величин, центральный момент первого порядка всегда равен нулю.
Рассеяние непрерывной случайной величины можно оценивать одним из следующих значений, словесные формулировки которых остаются прежними.
Среднее отклонение (мало удобная для вычислений величина)
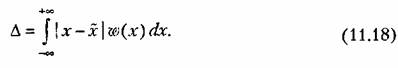
Дисперсия (наиболее удобная для вычислений величина)


Среднеквадратичное отклонение
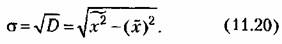
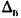 называется такая величина, при которой отклонения называется такая величина, при которой отклонения
 имеют одинаковую вероятность. имеют одинаковую вероятность.
Рассмотрим простейшие типовые законы распределения непрерывных случайных величин.
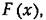 показанными на рис. 11.9. При этом на основании свойства (11,14) имеем показанными на рис. 11.9. При этом на основании свойства (11,14) имеем

Подсчитаем характерные значения. Среднее значение (математическое ожидание)

Среднее значение квадрата случайной величины (момент второго порядка)

Максимально возможное отклонение случайной величины от среднего значения в данном случае будет

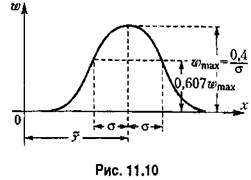
2. Нормальный закон распределения непрерывных случайных величин (закон Гаусса). Этот закон имеет вид
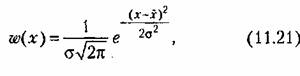
где а- среднеквадратичное отклонение, а х — математическое ожидание случайной величины.
График для этого закола изображен на рис. 11.10. Он имеет типичную колоко-лообразную форму.
Анализ условий возникновения нормального распределения показывает, что оно имеет место во всех тех случаях, когда случайная величина характеризует собой суммарный эффект большого числа независимых причин. Поэтому нормальное распределение весьма часто встречается на практике.
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
Для этого закона средпевероятное отклонение будет
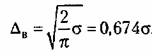
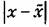 будет больше будет больше
За, очень мала, а именно:

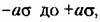 определится выражением определится выражением
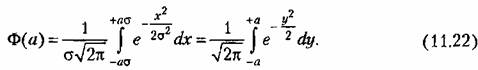
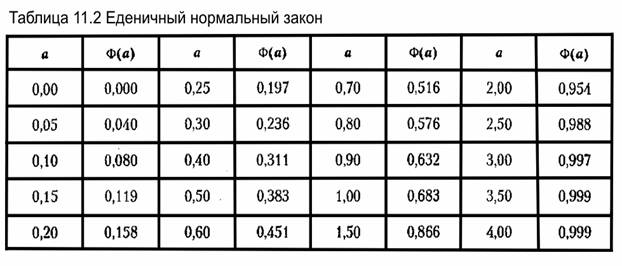
Для функции Ф (а) составлены подробные таблицы. В качестве иллюстрации приводится краткая табл. 11.2.
 Для относительных величин это соответствует неравенству Для относительных величин это соответствует неравенству
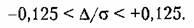

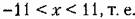
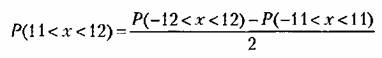
или для отклонений

Перейдя к относительным величинам, получаем в результате искомую вероятность
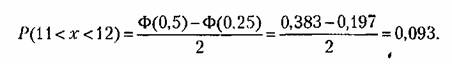
Характеристические функции. Введем в рассмотрение функцию § (/А,), связанную с плотностью вероятности г& (х) взаимным преобразованием Фурье:

Эта функция называется характеристической. Ее основные свойства следующие. Если случайная величина у = ах + й, то

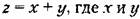 — независимые величины, то — независимые величины, то
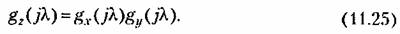
Для нормального закона распределения (11.21) характеристическая функция будет

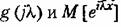 в цервой формуле (11.23) вряд Маклорена, имеем в цервой формуле (11.23) вряд Маклорена, имеем
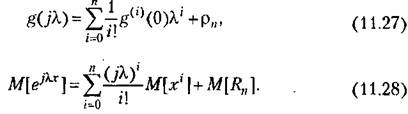
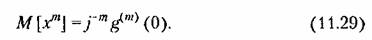
Аналогичным образом можно получить формулу для центрального момента т-го порядка:

Формулы (11.29) и (11.30) могут быть использованы для вычисления моментов.
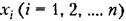 . Такая совокупность может быть представлена в виде матрицы-столбца. Если физические размерности всех величин одинаковы, то матрица-столбец может быть отождествлена с вектором. При разных размерностях переход к вектору может быть сделан после нормирования (введения весовых коэффициентов). . Такая совокупность может быть представлена в виде матрицы-столбца. Если физические размерности всех величин одинаковы, то матрица-столбец может быть отождествлена с вектором. При разных размерностях переход к вектору может быть сделан после нормирования (введения весовых коэффициентов).
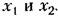 Для Для
 . Если величины . Если величины



и смешанного центрального момента
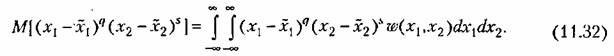
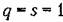 , то центральный момент второго порядка имеет особое значение и , то центральный момент второго порядка имеет особое значение и
носит название корреляционного момента:

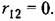
Иногда употребляется понятие коэффициента корреляции, представляющего собой относительное значение корреляционного момента:


 в приближенных расчетах в приближенных расчетах
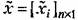 и матрицы корреляционных моментов и матрицы корреляционных моментов
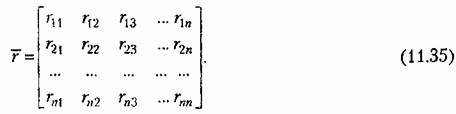

|