Теория систем автоматического управленияКорреляционная функция
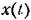 и и
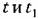 носит название корреляционной {автокорреляционной) функции. Она может быть найдена аналогично (11.31) из выражения носит название корреляционной {автокорреляционной) функции. Она может быть найдена аналогично (11.31) из выражения
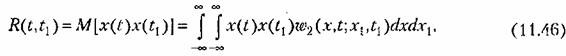
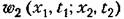 — двумерная плотность вероятности. — двумерная плотность вероятности.
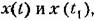 т. е. т. е.
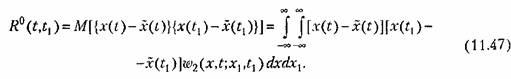
В этом случае корреляционная функция (11.46) может быть представлена в виде суммы
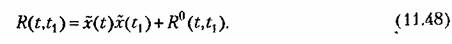
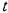 -Это есть мера связи между ними. -Это есть мера связи между ними.
Рассмотрим основные свойства корреляционных функций.
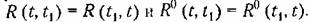
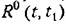 — дисперсию: — дисперсию:
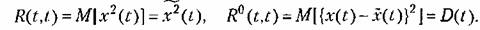
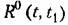 не изменится, если к случайной функции добавить произвольную неслучайную функцию. Это свойство не относится к функции не изменится, если к случайной функции добавить произвольную неслучайную функцию. Это свойство не относится к функции
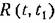 , так как добавление неслучайных величин к случайным изменяет начальные моменты. В этом случае корреляционная функция будет равна сумме корреляционных функций случайной и неслучайной функций. , так как добавление неслучайных величин к случайным изменяет начальные моменты. В этом случае корреляционная функция будет равна сумме корреляционных функций случайной и неслучайной функций.
Иногда в рассмотрение вводится нормированная корреляционная функция

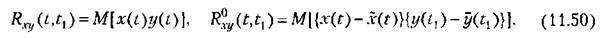
 называют некоррелированными. называют некоррелированными.
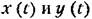 носят название коррелированных случайных функций. носят название коррелированных случайных функций.
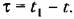
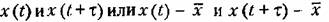
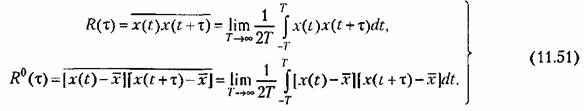
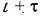 от предшествующего от предшествующего
значения в момент .
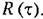
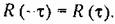 Это вытекает из самого определения корреляционной функции. Это вытекает из самого определения корреляционной функции.
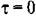 корреляционная функция дает средний квадрат случайной величины: корреляционная функция дает средний квадрат случайной величины:
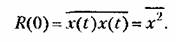
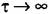 корреляционная функция дает квадрат среднего значения случай- пой величины. Докажем это. Па основании эргодической гипотезы корреляционная функция дает квадрат среднего значения случай- пой величины. Докажем это. Па основании эргодической гипотезы
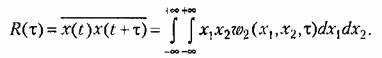
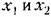 можно считать независимыми. Отсюда, принимая во можно считать независимыми. Отсюда, принимая во
внимание формулу (11.39) для независимых случайных величии, получим
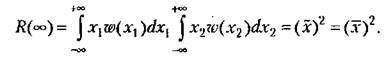
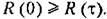 Докажем это. Рассмотрим очевидное неравенство Докажем это. Рассмотрим очевидное неравенство
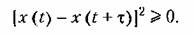
Сделаем преобразование
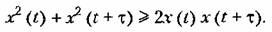
Возьмем теперь среднее но времени от правой и левой частей. В результате получим:
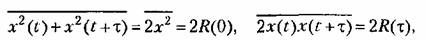
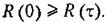
Значение корреляционной функции чаще всего будет тем меньше, чем больше промежутки времени т, так как связь между далеко отстоящими друг от друга значениями х будет обычно слабее.
Чем менее инерционен (более подвижен) объект наблюдения, тем быстрее убывает R (т) с увеличением т. Например, у самолета, как подвижной цели, связь между последующими и предыдущими положениями (при заданном т) будет тем меньше, чем он легче и маневреннее. Отсюда следует, что чем быстрее убывает корреляционная функция, тем более высокие частоты будут присутствовать в случайном процессе.
На рис. 11.14 в качестве примера приведены две корреляционные функции и две соответствующие им реализации процесса при одинаковых среднеквадратичных значениях случайной величины. Второй процесс по сравнению с первым имеет более тонкую структуру, т. е. в нем присутствуют более высокие частоты.
 Таким образом при известной корреляционной функции легко определяются следующие вероятностные характеристики; Таким образом при известной корреляционной функции легко определяются следующие вероятностные характеристики;
а) среднее значение (момент первого порядка)
б) среднеквадратичное значение
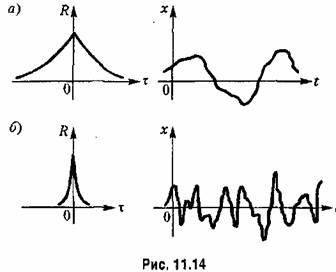
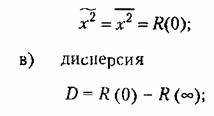
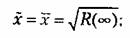 второго порядка) второго порядка)
г) среднеквадратичное отклонение
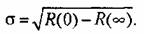
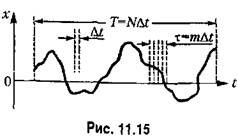
Корреляционную функцию можно найти на основании экспериментально снятой кривой случайного процесса при наличии достаточно длительной записи (рис. 11.15). Обработка имеющейся осциллограммы производится следующим образом. Весь интервал записи осциллограммы Г делится па Лг равных частей, длительность которых составляет
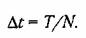
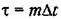 находятся средние значения произведений ординат: находятся средние значения произведений ординат:
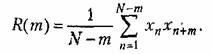
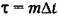
Корреляционную функцию можно найти по результатам эксперимента также при
помощи специальных приборов — корреляторов, которые автоматически вычисляют среднее произведение двух ординат осциллограммы, отстоящих друг от друга на расстояние т.
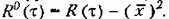
Можно также ввести в рассмотрение нормированную корреляционную функцию
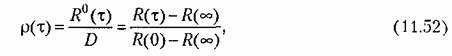
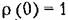
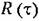 может вычисляться и для неслучайных функций времени. Рассмотрим несколько примеров. может вычисляться и для неслучайных функций времени. Рассмотрим несколько примеров.
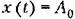 (например, для постоянного тока) корреляционная функция (например, для постоянного тока) корреляционная функция
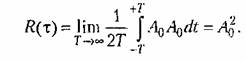
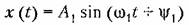
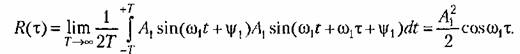
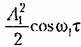 указывает на наличие в случайном процессе скрытой периодичности, которая может не обнаруживаться при первом взгляде на отдельные записи реализации случайного процесса. указывает на наличие в случайном процессе скрытой периодичности, которая может не обнаруживаться при первом взгляде на отдельные записи реализации случайного процесса.
3. Периодическая кривая, разлагаемая в ряд Фурье:
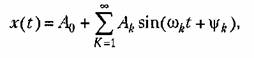
имеет на основании изложенного выше корреляционную функцию вида
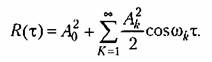
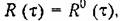 и при отсутствии скрытых периодичностей и при отсутствии скрытых периодичностей
имеет вид
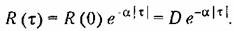
Иногда встречается корреляционная функция вида
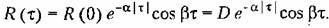
Эти выражения часто используются для аппроксимации корреляционных функций, полученных в результате обработки экспериментальных данных.
Для стационарных случайных процессов используется также понятие взаимной корреляционной функции, вводимой при рассмотрении каких-либо двух процессов
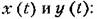
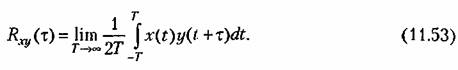
Для взаимной корреляционной функции существует следующее соотношение:
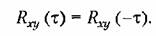
Кроме того, можно показать, что
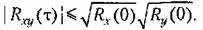
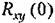 характеризует эту связь в один и тот же характеризует эту связь в один и тот же
момент времени. Примером таких двух взаимосвязанных случайных процессов могут служить две координаты пространственного положения подвижной цели.
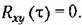 В связи с этим говорят, что процессы коррелированы или не коррелированы. Это означает наличие или отсутствие между ними статистической связи. В связи с этим говорят, что процессы коррелированы или не коррелированы. Это означает наличие или отсутствие между ними статистической связи.
Аналогично предыдущему можно также ввести понятие нормированной взаимной корреляционной функции.
|