Теория систем автоматического управленияРасчеты по минимуму среднеквадратичной ошибки
Если на автоматическую систему действуют одновременно полезный сигнал и помеха, то возникает задача оптимального расчета системы с тем, чтобы получить наименьшую результирующую ошибку. С точки зрения наилучшего воспроизведения полезного сигнала система должна иметь возможно большую полосу пропускания, а с точки зрения наилучшего подавления помехи система, наоборот, должна иметь возможно меньшую полосу пропускания. Критерием получения оптимального решения здесь будет минимальное значение результирующей ошибки системы, определяемой полезным сигналом и помехой.
Для случайных величин наиболее просто определить среднеквадратичную ошибку, поэтому ее и используют для опенки точности автоматической системы.
Рассмотрим расчет системы по критерию минимума среднеквадратичной ошибки при одновременном действии полезного сигнала и помехи.
Согласно этому критерию нежелательность ошибки пропорциональна квадрату ее величины. Такая постановка является часто логичной, но она не может, конечно, претендовать па полную универсальность. В некоторых случаях, например при стрельбе по какой-либо цели, все ошибки, большие некоторого значения, являются одинаково нежелательными. Однако средний квадрат ошибки системы управления

практически во всех случаях является наиболее просто вычисляемой величиной, что и определило использование этого критерия.
Возможны несколько формулировок задачи. Наиболее просто задача может быть сформулирована так. Если имеется какая-то система автоматического управления заданной структуры, то необходимо так выбрать параметры этой системы, чтобы получить минимум среднеквадратичной ошибки при заданных статистических характеристиках полезного сигнала и помехи.
Эта задача решается следующим образом. По спектральной плотности ошибки путем ее интегрирования находится дисперсия. Дисперсия получается зависящей от вероятностных характеристик полезного сигнала, помехи и параметров системы. Затем ищутся условия, которые должны быть наложены па параметры системы, чтобы получить минимум дисперсии. При достаточно простом выражении для дисперсии это может быть определено непосредственным дифференцированием и приравниванием нулю частных производных.
В более сложных случаях приходится искать минимум дисперсии путем числового задания интересующих параметров и построения соответствующих графиков, а также расчетом на ЭВМ.
 некоторой формулой преобразования некоторой формулой преобразования

 — преобразующий оператор. — преобразующий оператор.
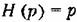 — задача дифференцирования, при Н {р)= — задача простого — задача дифференцирования, при Н {р)= — задача простого
 — статистическое упреждение (предсказание) и т. а. — статистическое упреждение (предсказание) и т. а.
На основании

изложенного ошибку системы можно представить в виде
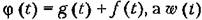 — весовая функция замкнутой системы. — весовая функция замкнутой системы.
Подставляя (11.130) и (11.131) в формулу (11.129), получаем
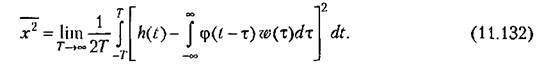
Задача заключается в том, чтобы найти частотную передаточную функцию замкнутой системы, связанную с весовой функцией преобразованием Фурье

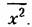
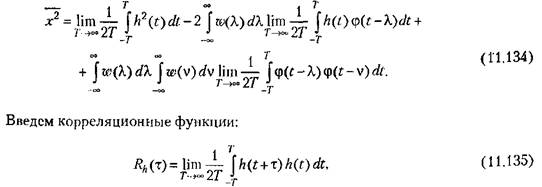
Раскроем в выражении (11.132) скобки и изменим порядок интегрирования:
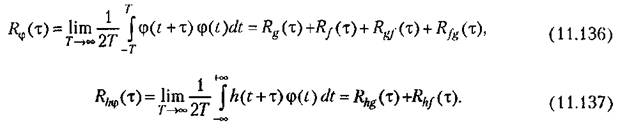
 того, того,

В результате выражение (11.134) можно преобразовать к виду
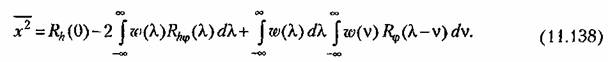
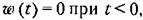 то нижние пределы интегрирования в (11.138) надо положить равными нулю. В результате получим то нижние пределы интегрирования в (11.138) надо положить равными нулю. В результате получим
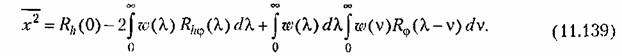
Из последнего выражения видно, что оптимальная весовая функция, соответствующая минимуму среднего квадрата ошибки, определяется только видом корреляционных функций полезного сигнала и помехи.
Можно показать [88], что необходимое и достаточное условие минимизации выражения (11.139), которое должно быть наложено на весовую функцию, заключается в том, чтобы она была решением интегрального уравнения Вииера-Хопфа
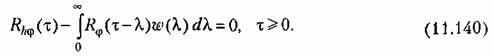
Оптимальная передаточная функция (11.133), соответствующая оптимальной весовой функции, являющейся решением уравнения (11.140), может быть представлена в виде

 т. е. в так называемом случае оптимального сглаживания, имеем т. е. в так называемом случае оптимального сглаживания, имеем

В этом случае решение (11.1-11) может быть представлено в более простом виде:

Числитель этого выражения определяется следующим образом. Рассмотрим следующее выражение:

 — —
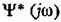 . Тогда . Тогда

При реализации в системе оптимальной передаточной функции получится теоретический минимум среднего квадрата ошибки. Этот минимум определяется выражением
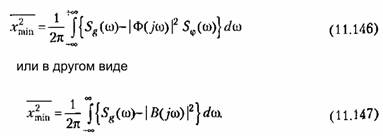
Рассмотрим иллюстративный пример. Предположим, что полезному сигналу и
помехе на входе системы соответствуют спектральные плотности:

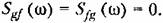 Иайдйм спектральную плотность, соответствующую (11.136): Иайдйм спектральную плотность, соответствующую (11.136):

Отбросив первый член в скобках, соответствующий полюсу в нижней полуплоскости, находим числитель искомой передаточной функции (11.143):

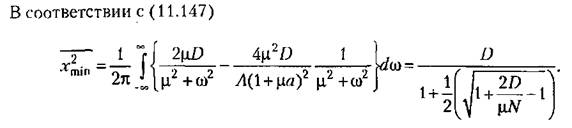
Нахождение оптимальной передаточной функции еще не означает, что реальная автоматическая система может быть выполнена оптимальной, так как реализация ее может быть сопряжена с большими трудностями. Оптимальную передаточную функцию, за исключением простейших случаев, следует считать идеальной функцией, к которой но возможности надо стремиться при выполнении реальной автоматической системы. Теория оптимальных систем излагается в работах [22, 88, 89].
|